Mathematics for the liberal arts (2013)

Part II. TWO PILLARS OF MATHEMATICS

Chapter 5. NUMBER THEORY

5.8 The Fundamental Theorem of Arithmetic

The Theorem: Prime Factorization

The Fundamental Theorem of Arithmetic starts with an observation we recorded in Section 5.5—that every integer greater than 1 is divisible by a prime. So let n be an integer, with n > 1. Then there is some prime p such that p | n. Now look at n/p. It is possible that this is 1, so that n = p. If not, we can find an integer q such that q divides n/p. We can then repeat this process on n/(pq); if n/(pq) = 1 then n = pq, else there is a prime r such that r divides n/(pq), and so on. Eventually we will have expressed n as the product of primes.

The Fundamental Theorem of Arithmetic. Let n be any integer greater than 1. Then n can be expressed as a product of primes (with perhaps only one prime). Furthermore, this expression is unique, up to the order of the primes.

The product from the theorem is called the prime factorization of n.

The history of the Fundamental Theorem of Arithmetic is somewhat murky. Elements of the theorem can be found in the works of Euclid (c. 330–270 BCE), the Persian Kamal al-Din al-Farisi (1267-1319 CE), and others, but the first time it was clearly stated in its entirety, and proved, was in 1801 by Carl Friedrich Gauss (1777–1855). A formal proof is beyond the scope of this text.

EXAMPLE 5.16

Find the prime factorization of 24.

Solution: First, we notice that 2 | 24, so divide 24 by 2:

Next, we need to look at 12. Since 2 also divides 12,

Again, 2|6, so

Now 3 is prime, so we are done. The prime factorization is 24 = 2³ · 3.

EXAMPLE 5.17

Factor (i.e., find the prime factorization of) 1001.

Solution: It may not be obvious what, if any, prime divides 1001. So let us start with the smallest, then systematically work our way up. Since 1001 ends in an odd digit, 2 is not a divisor. The next prime is 3. Here is a trick for determining divisibility by 3; if 3 divides a number, it must divide the sum of the digits of that number. Here the sum of the digits isl + 0 + 0 + l = 2, which 3 does not divide, so 3 is not a divisor of 1001. Next is 5, which does not divide 1001, since 1001 does not end in 0 or 5. The next prime is 7. We are in luck here: 1001 = 7 · 143. (Check!). So now we need only work with 143.

To factor 143, we do not need to check the primes 2, 3, and 5 again. If any of them divided 143, then they would divide its multiple 1001, which we know is not the case. So let’s start with 7. You can check that 7143. So we go to the next prime, 11. Here is success: 143 = 11 · 13. Finally, 13 is itself prime, so we have our prime factorization:

EXAMPLE 5.18

Factor 101.

Solution: Again, we start with the smallest prime and work our way up. You can check that none of 2, 3, 5, or 7 divides 101. Fortunately, we do not have to check any more primes. Why not? The next prime to check is 11. Suppose that 11|101, say 101 = 11x. We know that x cannot be less than 11, since we have checked all the primes less than 11. So x ≥ 11. But then 101 = 11x ≥ 11 · 11 = 121, but of course 101 is less than 121. By a similar argument, we know that no prime greater than 11 divides 101. We are done; 101 is prime.

The general principle is this: in checking primes for divisors, we need only check primes up to the square root of our number. To see this, suppose that we are factoring n, and checking p, having already verified that no number less than p divides n. If p | n, then n = px, for some integer x. Since we have checked all smaller numbers, we know that x ≥ p. Then n = px ≥ p², so , i.e., p is no larger than the square root of n.

If you find factoring numbers difficult, you are not alone. Computers find it hard as well, much harder than multiplying numbers. In fact, one of the most famous and widely used methods of encrypting data, called RSA encryption(for inventors Ronald L. Rivest, Adi Shamir, and Leonard Adleman), is based on the difficulty of factorization.

Using Prime Factorization

You may not be surprised to learn that something called the Fundamental Theorem of Arithmetic is useful. There are many questions about an integer that can be reduced to questions about its prime factors. We will look at three applications of the theorem.

For our first application, we will look at the divisors of a number. Suppose that n is some positive integer, with prime factorization n = and k is a positive divisor of n. From the uniqueness of the prime factorization, we know that the only primes that can divide k are p₁ and p₂. So we can write k = where either of s or t can be 0. (Recall that x⁰ = 1 for any x ≠ 0, so if s, say, is 0, that means that p₁ is not a factor of k.) Furthermore, doesn’t divide n, so s ≤ 1. Similarly, t ≤ 2. Therefore, the complete list of divisors of n is

or, rewritten,

Prime Factorization and Divisors. Let n be a positive integer, with prime factorization . Then the positive divisors of n are the integers with 0 ≤ s_i ≤ r_i, for i = 1, 2, …, m.

We can use this to understand more about greatest common divisors. Let’s do an example.

EXAMPLE 5.19

Find gcd(136,52).

Solution: First, you can check that the prime factorizations of our numbers are

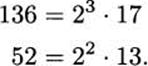
It is useful to rewrite this so that both numbers have the same list of primes:

where again we have used p⁰ = 1 for any p. Now, by our result above, the divisors of 136 are

where s₁ is between 0 and 3, s₂ is 0, s₃ is 0 or 1.

Similarly, the divisors of 52 are

where t₁ is between 0 and 2, t₂ is 0 or 1, and t₃ is 0.

A common divisor has to satisfy both of these, so the largest one is

Here is the general rule.

Prime Factorization and Greatest Common Divisors. Let a and b be integers greater than 1. Let their prime factorizations be

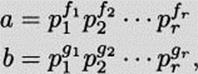
where some of the f_i or g_i may be 0. Then the greatest common divisor of a and b is given by

where h_i is the minimum of f_i and g_i, for i = 1, 2, …, r.

If you find this notation confusing, here is another way of thinking about it. To find the gcd of a and b, first find their prime factorizations. Then the prime factorization of their gcd contains just the primes that divide both a and b, and the power of each such prime is the lesser of the powers of that prime in the factorizations of a and b.

EXAMPLE 5.20

Find the greatest common divisor of 990 and 4725.

Solution: First we factor the two numbers.

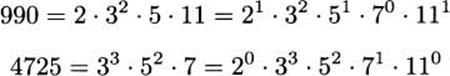
Then we read off the gcd, taking the minimum power of each factor.

Recall that the least common multiple of integers a and b, written lcm(a, b), is the smallest positive integer d such that a | d and b | d. The Fundamental Theorem of Arithmetic can also be used to understand least common multiples.

Prime Factorization and Least Common Multiples. Let a and b be integers greater than 1. Let their prime factorizations be

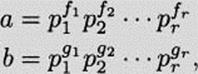
where some of the f_i or g_i may be 0. Then the least common multiple of a and b is given by

where h_i is the maximum of f_i and for i = 1,2,…, r.

EXAMPLE 5.21

Find the least common multiple of 990 and 4725.

Solution: This is easy. Using the factorizations from the last example, we take maximum powers, instead of the minimum. The least common multiple is

EXERCISES

5.44 Find the prime factorization.

a) 16

b) 59

c) 72

d) 105

e) 1633 (Hint: 3 · 1633 = 4899 = 70² – 1.)

5.45 List all the positive divisors of 675.

5.46 List all the divisors of 675.

5.47 How many positive divisors does 1,000 have?

5.48 Find the gcd of 2² · 3³ · 11² · 17 and 2 · 3⁴ · 17⁶ · 71.

5.49 Find the gcd and 1cm of 198 and 429.

5.50 Find the gcd and 1cm of the three numbers 198, 429, and 156.

5.51 Express 1,000,000,000 as the product of two integers, neither of which contains a 0 digit.

5.52 A: How many kids do you have?

B: I have three.

A: What are their ages?

B: The product of their ages is 36. The sum of their ages is my house number, which of course you know.

A: Of course. But I need more information.

B: The oldest has red hair.

A: Thank you, now I know.

What are the ages of the kids?