Mathematics for the liberal arts (2013)

Part II. TWO PILLARS OF MATHEMATICS

Chapter 5. NUMBER THEORY

5.11 Pythagorean Triples

Recall the Pythagorean Theorem: If a right triangle has legs of lengths a and b, and hypotenuse of length c, then a² + b² = c². As far back as the old Babylonian period, almost 4000 years ago, mathematicians were looking for triples of integers that satisfied this equation. In other words, they were looking at the Diophantine equation x² + y² = z². Solutions to the Diophantine equation are called Pythagorean triples. A couple of examples are the 3–4–5 triangle and the 5–12–13 triangle. You can check any of these by summing squares. For example,

Is there a formula to give all Pythagorean triples?

Given any Pythagorean triple, we can multiply all three numbers by any positive integer and obtain another Pythagorean triple. For example, the 6–8–10 triangle is created by doubling the 3–4–5 triangle. This amounts to enlarging the triangle but keeping its shape. We say that a Pythagorean triple is primitive if the three side lengths have no common factor.

There is a simple method, called Euclid’s formula, for generating all primitive Pythagorean triples.

Euclid’s Formula. All primitive Pythagorean triples are given by a = m² – n², b = 2mn, and c = m² + n², where m and n are positive integers with no common factor, m > n, and one of m and n is even and the other is odd.

Let’s do an example of the formula. Let m = 5 and n = 2. These numbers have no common factor, and one is odd and the other even. According to Euclid’s formula, we obtain the Pythagorean triple 21, 20, and 29. Let’s check:

And it is easy to check that the numbers 21, 20, and 29 have no common factor.

Proof It is a simple matter to prove that Euclid’s formula always gives us a Pythagorean triple. Just sum the squares:

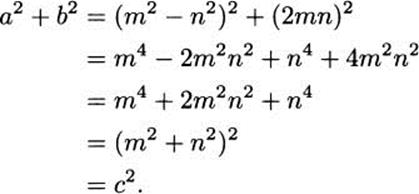
Now we will show that the triple a, b, c is primitive (the numbers have no common factor). We will give a proof by contradiction, assuming that our result is false and showing that this leads to a contradiction.

Suppose that a, b, and c have a common factor. Then c has a common factor with a. Such a factor may be a prime number or it may be a composite number (a product of primes). However, if the common factor is a composite number, then that number’s prime factors also divide a and c. Hence, we may assume that a and c have a prime factor in common.

Let’s call this common prime factor p. Notice that p cannot equal 2, since c is an odd number (why?). We will show that p is also a prime common factor of m and n, which is impossible because m and n have no common factor; this contradiction will show that the assumption that a, b, and c have a common factor is false.

Since p divides m² + n² and m² – n², it follows that p divides their sum, 2m², and their difference, 2n². Thus p divides m², and therefore p divides m. By the same reasoning, p divides n.

This is what we wanted to show. Thus, p is a common factor of m and n, which isn’t possible (since m and n have no common factor). Therefore, our original assumption that a, b, and c have a common factor is false, and we conclude that (a, b, c) is a primitive Pythagorean triple.

We have proven that Euclid’s formula always generates a primitive Pythagorean triple, but we haven’t proven that all primitive Pythagorean triples can be obtained in this way. We now do this. Suppose that a² + b² = c², where a, b, and c are positive integers with no common factor.

First we note that a and b cannot both be even, since a, b, and c do not share the common factor 2. Suppose that a and b are both odd, say a = 2k + 1 and b = 2l + 1. Then

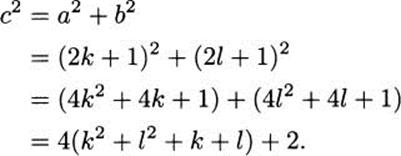
Note that 4(k² + l² + k + l) + 2 is even, but not divisible by 4 (else 2 would be divisible by 4). This is a problem, however, since this number is also c², and every even square must be divisible by 4. We conclude, then, that a and bcannot both be odd. Since we already showed that they could not both be even, one must be even, and one odd.

Suppose, without loss of generality, that a is even and b is odd. Then we have

Since b and c are odd (check!), both c + b and c – b are even, so we can write

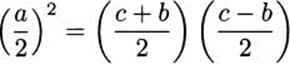
where the terms in parentheses are integers.

Next, we see that (c + b)/2 and (c – b)/2 are relatively prime. Suppose that some number d divides both. Then d divides (c + b)/2 + (c – b)/2 = c and d divides (c + b)/2 – (c – b)/2 = b, so that d would be a common factor of a, b, and c, which we assumed cannot happen.

So we have a product of two relatively prime integers equal to a perfect square, (a/2)². It follows that both integers, that is, (c + b)/2 and (c – b)/2 are perfect squares (why?).

Let’s set

Solving for c and b, and then a, we have

Clearly, m > n. And m and n can have no common factor, or else a, b, and c would have a common factor (and we have assumed that they do not). Finally, we note that one of m, n is even and the other odd. (Details of this are left to the exercises.) This establishes the formula for Pythagorean triples.

EXERCISES

5.60 Use Euclid’s formula to find the primitive Pythagorean triangle corresponding to the choice m = 10, n = 7.

5.61 What choice of m and n in Euclid’s formula gives the 3–4–5 right triangle?

5.62 Find all the primitive Pythagorean triples where the hypotenuse is at most 100.

5.63 Show that, if we define m and n as in the proof,

one of them is even and the other is odd. (Hint: since b and c are both odd, we can write b = 2k + 1 and c = 2l + 1 for integers k and l. See how the parity of m and n depends on the parity of k and l.)