Mathematics for the liberal arts (2013)
Part II. TWO PILLARS OF MATHEMATICS
Chapter 5. NUMBER THEORY
5.14 Arithmetic with Congruences
One of the main reasons that congruence is useful is that most arithmetic on congruence classes is much like our familiar arithmetic.
Addition, Subtraction, and Multiplication Are Easy
Let a, b, c, and d be any integers, m a positive integer. Suppose that a ≡ b (mod m) and c ≡ d (mod m). Then
i. a + c ≡ b + d (mod m)
ii. a – c ≡ b – d (mod m)
iii. ac ≡ bd (mod m).
Proof. This is pretty straightforward. We will prove (i). Since a ≡ b (mod m) and c ≡ d (mod m), there are integers k and l such that a = b + km and c = d + lm. Then
![]()
Therefore a + c ≡ b + d (mod m).
![]()
![]() EXAMPLE 5.32
EXAMPLE 5.32
If a ≡ 5 (mod 9), what is the remainder of 17a on division by 9?
Solution: We use part (iii) of the theorem. Note that we have a ≡ 5 (mod 9) and 17 ≡ 8 (mod 9). So we have
![]()
Definition: What does this theorem do for us? It means, for example, that the congruence class of the sum of two numbers depends only on the congruence classes of the two numbers, not on the particular numbers themselves. So it makes sense to talk of the sum of two congruence classes. Similarly, we can subtract and multiply classes. Using the notation we introduced in the last section, we can define
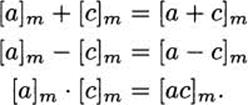
In other words, we have arithmetic on congruence classes.
![]() EXAMPLE 5.33
EXAMPLE 5.33
Revisiting the last example, we have
![]()
Notation: When the modulus is clear, we can skip the subscript, e.g., write [17a] instead of [17a]9.
![]() EXAMPLE 5.34
EXAMPLE 5.34
Suppose that x is a number congruent to 3 mod 5. What is the congruence class of 2x2 – 7x + 5?
Solution: To solve this, first note that [x2] = [x][x]. We will denote this by ([x])2. So
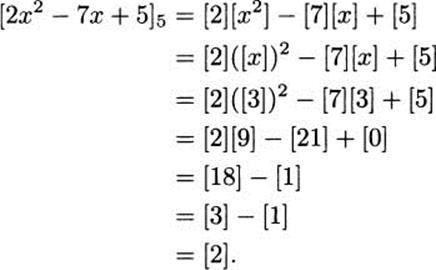
Using Congruence Arithmetic
![]() EXAMPLE 5.35
EXAMPLE 5.35
Prove that no square has remainder 2 or 3 when divided by 4.
Solution: Suppose we have a square, say x2. Let’s consider all possible least residues (i.e., remainders) of x mod 4.
If x mod 4 = 0, then [x2]4 = [x]4[x]4 = [0]4[0]4 = [02]4 = [0]4.
If x mod 4 = 1, then [x2]4 = [12]4 = [1]4.
If x mod 4 = 2, then [x2]4 = [22]4 = [0]4.
If x mod 4 = 3, then [x2]4 = [32]4 = [1]4.
Thus the remainder is always 0 or 1.
![]()
Congruence Modulo 9: If you add up the digits of a positive integer, the sum is in the same congruence class as the original integer. For example,
![]()
Why does this work? Because [10]g = [l]g. For our example,
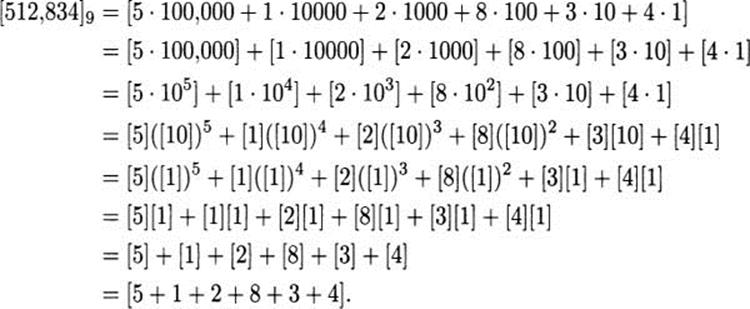
A Divisibility Rule for 9: Because the sum of the digits of a number n is congruent to n, we can easily determine whether a number is divisible by 9: n is divisible by 9 if and only if the sum of its digits is divisible by 9. For example, let n = 12,345,623. Adding the digits, gives
![]()
Since 26 is not divisible by 9, neither is 12,345,623.
Casting Out Nines: If you can find a set of digits that add up to 9, you can throw them away (cast them out), without changing the congruence class. For example, in 512,834, the digits 1 and 8 add up to 9, so we can cast them out: 512,834 ≡ 5234 (mod 9). This works because the sum of the digits in the new number differs only by 9, which is 0 mod 9, so it doesn’t affect the congruence class of the sum of the digits. Thus it doesn’t affect the congruence class of 512,834.
Continuing with our example, 2 + 3 + 4 = 9, therefore we can cast these digits out: 5234 ≡ 5 (mod 9), hence 512,834 ≡ 5 (mod 9), which is the same answer we got above.
Checking Calculations By Casting Out Nines: An old way (pre-calculator) for checking arithmetic is based on casting out nines. As an example, consider this addition.
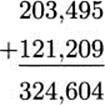
Casting out nines, we see that 203,495 ≡ 5 (mod 9), that 121,209 ≡ 6 (mod 9), and 324,604 ≡ 1 (mod 9). But [5]9 + [6]9 ≠ [1]9, so the addition must be wrong. The correct sum is 324,704.
Residues of Negative Integers: We saw in the last section that finding congruence classes of negative numbers could be tricky. But there is an easy way around the difficulty. Consider [– 8]5. We can write this as
![]()
To find the least residue of –8 mod 5, find the least residue of 8, and subtract it from 5.
Here is another example: –102 (mod 7) = 7 – 102 (mod 7) = 7 – 4 = 3.
EXERCISES
5.72 Find the congruence classes.
a) [31]8 + [17]8
b) [2]3[22]3 – [1]3
c) [– 9]7 – [–2]7
5.73 What is the least residue of –26 modulo 17?
5.74 If x ≡ 5 (mod 8), what is [32x3 – 45x2 + 232x – 118]8?
5.75 What day of the week will it be exactly one year from today?
5.76 Find all integers x such that x2 + 2x + 1 ≡ 2 (mod 7).
5.77 The method of checking calculations by casting out nines is not perfect; there are cases in which the calculation is incorrect but the method does not reveal this fact. Find such an example.
5.78 Is there any number other than 9 for which something like casting out nines works?
5.79 How can you change a dollar into 26 coins? (Hint: what are the possible numbers of pennies?)
5.80 Recall that n! is the product of the first n positive integers. For example, 2! = 1 · 2 = 2 and 3! = 1 · 2 · 3 = 6. Find the remainder of 1! + 2! + 3! + … + 100! upon division by 12.
5.81 Let a, b, c, and d be any integers, and m a positive integer. Suppose that a ≡ b (mod m) and c ≡ d (mod m). Show that the following congruences are always true.
a) a – c ≡ b – d (mod m)
b) ac ≡ bd (mod m)