Mathematics for the liberal arts (2013)
Part II. TWO PILLARS OF MATHEMATICS
Chapter 5. NUMBER THEORY
5.15 Division with Congruences; Finite Fields
The Problem
You may have noticed the conspicuous absence of division from the congruence arithmetic so far. The reason for this is familiar: division presents special problems with integers.
What would the division equivalent of the basic result of Section 5.13 look like? Perhaps:
But this only makes sense if a/c and b/d are integers. But the situation is more complicated even than this. For example, let a = 4, and b, c, d, and m all equal 2. Then a ≡ b (mod m) and c ≡ d (mod m), but although a/c and b/d are integers in this case, still a/c 
b/d (mod m).
Here is another example to illustrate the difficulty. Let a = 2, b = 9, c = 12, and m = 6. Then ab ≡ ac (mod m), but b c (mod m). (Check!) So we can’t cancel. Of course cancelling is equivalent to dividing, so this shouldn’t surprise us. There is one important case, however, in which cancellation does work.
GCDs to the Rescue
Let ab ≡ ac (mod m) and suppose that a and m are relatively prime. Then b ≡ c (mod m).
Proof. Recall the theorem of Section 5.6: If r | st, and r and s are relatively prime, then r|t. We will use this result.
Now ab ≡ ac (mod m), so m | (ab – ac), i.e., m | a(b – c). Since a and m are relatively prime, the theorem applies to give us m | (b – c). But this tells us that b ≡ c (mod m).
EXAMPLE 5.36
Solve 2x ≡ 14 (mod 25) for x.
Solution: Since 2 and 25 are relatively prime, we can divide by 2, to get x ≡ 7 (mod 25). So x is any number in [7]25.
EXAMPLE 5.37
Solve 4x = 1 (mod 6) for x.
Solution: Since 4 and 6 are not relatively prime, the theorem does not apply. In fact, there are no solutions. If x were to work, then we would have 6 | (4x – 1). But 4x – 1 is odd, and 6 does not divide any odd number.
EXAMPLE 5.38
Solve 6x ≡ 2 (mod 8) for x.
Solution: Since 6 and 8 are not relatively prime, the theorem doesn’t apply. But in this case, there are solutions. Let’s systematically consider each congruence class mod 8.
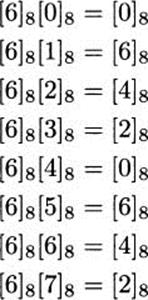
There are actually a lot of solutions: all the numbers in [3]8 and all the numbers in [7]8.
The last set of examples suggests that a variety of things can happen when you try to divide. We will concentrate on a particular, very important case: when m is prime.
Let p be a prime, and consider division modulo p. First, consider the implications of the last theorem on canceling in the equation ab ≡ ac (mod p). Whenever p does not divide a, because p is prime, a and p must be relatively prime, so b ≡ c (mod p). Therefore we can cancel.
Finite Fields
Consider the equation [a]p[x]p = [b]p, where p is prime, and a and b are fixed. Can we solve this for [x]p? Thinking of regular integer arithmetic, we want to write [x]p = [b]p/[a]p. But what in the world is [b]p/[a]p? It certainly is not [b/a]p, since b/a may not be an integer.
Let us jettison the subscript p. So our problem is to solve the equation [a] [x] = [b].
EXAMPLE 5.39
Solve the equation [4][x] = [1], where p = 5.
Solution: Note that there are only five possible solutions, since there are only five congruence classes, corresponding to the remainders 0,1, 2, 3, 4. So let’s try them.
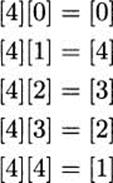
We have our solution: [x] must be [4].
EXAMPLE 5.40
Solve the equation [4][x] = [222], where p ≡ 7.
Solution: First, since 222 ≡ 5 (mod 7), we can restate this as: solve [4][x] = [5]. Let us try each of the five possible solutions for [x].
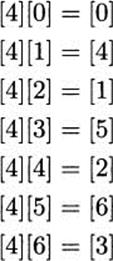
Our solution is [x] = [3].
If you do a few computations like the last two, a pattern emerges.
Suppose [a] ≠ [0]. Then the products [a][0], [a][1],…, [a][p – 1] are all distinct.
Proof. Suppose that two of the products were the same, say [a] [b] = [a] [c], where b and c are in {0, 1,… ,p – 1}. Then ab ≡ ac (mod p). But since [a] ≠ [0], a and p are relatively prime. Hence we can cancel: b ≡ c (mod p). But band c are in {0,1,… ,p – 1}, and no two of those remainders are congruent. Therefore b – c. This proves the theorem.
EXAMPLE 5.41
Let us look at the products in the case where p = 5 and a = 2.
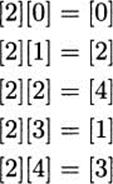
Notice that all the products are distinct, as advertised. But notice something else. Since there are only five possible products (the five congruence classes), every congruence class must appear as one of the products. This means that the equation [2][x] = [b] always has a solution, because one of the products has to be [b]. This argument generalizes to every prime, and we have the following satisfying result.
Let [a] ≠ [0]. Then the equation [a][x] = [b] has exactly one solution.
Definition. Let [a] ≠ [0]. Then we define the quotient [b]/[a] to be the solution to [a][x] = [b]. Note that we do not have a quotient when [a] ≠ [0]. But this is a form of our familiar inability to divide by 0.
EXAMPLE 5.42
Find the quotients, where p = 5.
(a) [3]/[2]
(b) [0]/[2]
(c) [1]/[2]
Solution: We can read these off of our products in the last example.
(a) [3]/[2] = [4] because [2][4] = [3]
(b) [0]/[2] = [0] because [2][0] = [0]
(c) [1]/[2] = [3] because [2][3] = [1]
EXAMPLE 5.43
Solve [5][x] – [3] = [28], where p = 11.
Solution: If we add [3] to both sides of the equation, we get
using 31 mod 11 = 9. Now we can check all the classes [0], [1], …, [10] one by one, to solve [5][x] = [9], until we find a solution: [x] = [4]. By our last result, we know that this is the only solution.
It is always a good idea to double-check our solution in the original equation:
using 17 ≡ 28 (mod 11).
Let us pause and admire the scenery. Consider how far we have come. When p is a prime, we can add, subtract, multiply, and divide just as we can with real numbers. And we can solve linear equations.
Mathematicians have a name for such a structure: it is called a field. The set of congruence classes modulo p, with the arithmetic we have defined, is an example of a field. It is called a finite field because there are a finite number of congruence classes. Finite fields have found some important applications in the last 100 years. For example, statisticians use finite fields in design theory, to design good statistical experiments.
Another application is error-correcting codes, which are based on finite fields. These are used to encode messages in possibly noisy channels, in such a way that if a small error is made in transmission, the error can be detected and corrected. For example, consider communicating with a spaceship orbiting Saturn. If a message received from the spaceship is slightly garbled, we can ask for the message to be sent again. But then we need to wait hours for a response, since Saturn is so far away. If, instead, the message was encoded using an error-correcting code, we can immediately correct the error and read the message. Similarly, if your computer mistakenly flips a bit (changes a 0 to 1 or vice versa), it is automatically detected and corrected. In fact, error-correcting codes were invented for this use, by Richard Hamming in the late 1940s.
As a final application, we consider a widely used error-detecting code, i.e., a code that detects errors, but cannot correct them.
International Standard Book Number (ISBN): Every book has an ISBN, which is used to identify the book uniquely. These numbers employ modular arithmetic to detect copying errors. Below is the system used until 2007. The current version is a slight modification of it.
An ISBN is a ten-digit number. The first nine digits identify a geographical grouping, publisher, and title. The tenth digit is a check digit. The check digit is chosen as follows. We start with the first nine digits a1a2a3a4a5a6a7a8a9. Then we pick the tenth digit, a10, so that
In other words, 11 divides the sum. One little twist: the check digit may have to be 10, in which case we write it as X.
To simplify our notation, let us write
and
so that chk(A) ≡ 0 (mod 11). The number chk(A) is called the checksum of A.
As an example, consider the ISBN number 0-672-51831-7, where 7 is the check digit. (The dashes in the ISBN help in identifying the grouping, publisher, and title. They are not important to us.) Then
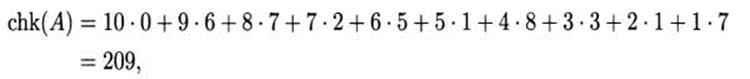
and 209 is divisible by 11, since 209 = 11 · 19.
Here is another example. Suppose that the ISBN starts out 0-471-15408. What is the check digit? Let us call it y. Then
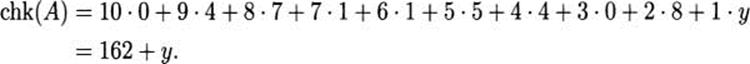
So 162 + y is a multiple of 11. It is easy to check that the next multiple of 11 above 162 is 165. Therefore, y = 3 and the ISBN is 0-471-15408-3.
What does the check digit do? It helps to detect the two most common types of copying errors: mis-typing a digit, or switching two digits. Let us see how that works.
First, suppose that we mistakenly write the wrong third digit. Let
where a′3 ≠ a3 The claim is that chk(A′) cannot be divisible by 11, in other words, that we can see that an error occurred. Suppose not, that chk(A’) is divisible by 11. We will show that this leads to a contradiction.
Since chk(A) is also divisible by 11, we have
or
Now chk(A) and chk(A’) differ in only the third position, so all the other terms of chk(A’) – chk(A) cancel, and we are left with chk(A’) – chk(A) = 8a′3 – 8a3 = 8(a′3 – a3). Hence
In congruence notation, [8][a′ –3 – a3] = [0], where p = 11. We know that the equation [8][x] = [0] has only one solution, however, namely, [x] = [0]. Therefore [a′3 – a3] = [0], so that a′3 – a3 must be divisible by 11. Both a3 and a′3 are between 0 and 10, so a′3 – a3 is between – 10 and 10. Now the only multiple of 11 in this range is 0, so a′3 – a3 = 0, i.e., a′3 = a3. But we started out assuming that a′3 ≠ a3, so we have a contradiction. Therefore, this error would be detected.
A similar argument can be used to see that the checksum detects the error when we switch two digits. For example, suppose that we have switched the first and third digits, say,
and
Arguing as above, if the error cannot be detected, then we have
which in this case gives us
(Check!) Rewriting,
or
In congruence notation, [2][a3 – a1] = [0], where p = 11. As before, this implies that [a3 – a1] = [0], so a3 = a1. So what? Well, we started out assuming that we switched a1 and a3, and concluded that, if this was not detected, then a3 = a1. But if we switch two identical digits, nothing is changed. If there is a change, the checksum will detect it.
EXERCISES
5.82 Solve for x.
a) 3x ≡ 12 (mod 16)
b) 2x ≡ 1 (mod 10)
c) 3x ≡ 6 (mod 9)
d) 3x + 1 ≡ 2 (mod 7)
5.83 Solve for [x].
a) [2]3[x] = [1]3
b) [2]6[x] = [1]6
c) [5]11[x] = [3]11
d) [2]7[x] – [5]7 = [1]7
5.84 In Section 5.11 we wrote out addition, subtraction, and multiplication tables for arithmetic modulo 2. Write out the corresponding tables for arithmetic in the field of congruence classes modulo 7.
5.85 Since 7 is prime, we can divide its congruence classes. Write out a division table for arithmetic mod 7. There is a useful shortcut, using quotients of the form [1]/[a]. For example, you can see that [1]/[5] = [3]. We can use this to divide any other class by [5]. Here are two samples.
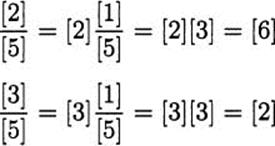
5.86 Use the tables from the last two exercises to solve for [x].
a) [4][x] = [3]
b) [x] – [5] = [2]
c) [2][x] + [5] = [1]
d) [x]2 – [3][x] + [2] = [0]
5.87 Compute the check digit y of this ISBN: 0-8053-0490-y.
5.88 Which of the following ISBNs contain an error?
a) 8-0027-1331-9
b) 0-1400-2547-2
c) 0-321-38700-X (Remember that X stands for 10.)