Mathematics for the liberal arts (2013)

Part I. MATHEMATICS IN HISTORY

Chapter 1. THE ANCIENT ROOTS OF MATHEMATICS

1.5 The Slow Decline

The Greeks held the geometer in the highest honor, and, to them, no one came before mathematicians. But we Romans have established as the limit of this art, its usefulness in measuring and reckoning. The Romans have always shown more wisdom than the Greeks in all their inventions, or else improved what they took over from them, such things at least as they thought worthy of serious attention.

CICERO (106–43 BCE)

Late ancient Greek mathematics.

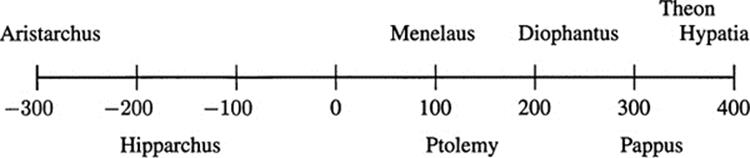
Progress is not inevitable. Mesopotamian mathematics reached a peak in the Old Babylonian period (c. 1900–1550 BCE), then stagnated for more than a thousand years. Egyptian mathematics also stagnated after the early part of the second millennium BCE.

Ancient Greek mathematics achieved its greatest heights in the 3rd century BCE. The brilliance of this period was not matched again until the 17th century. Research did not entirely cease, however, at least for six hundred years or so. There were notable developments in trigonometry and number theory, and some very influential texts appeared in this period.

The Roman Empire

Roman citizens overthrew their Etruscan rulers and established a republic in 509 BCE. In the ensuing centuries, they gradually extended their power, to the rest of Italy, then the western Mediterranean, then the eastern Mediterranean. By the middle of the first century BCE, they ruled the entire Mediterranean, including Asia Minor and Egypt. By that time, they had also lost their republic, in which much of the power was entrusted to an elected senate, to be replaced ultimately by an imperial system. Starting with Julius Caesar (100–44 BCE), the Romans proceeded to conquer what is now France, southern Germany, and Britain.

The height of the Roman empire was in the years of the Pax Romana (“Roman peace”) from 27 BCE to 180 CE. In these years, Rome was ruled by a succession of emperors. The “peace” didn’t mean no wars. There were still wars of conquest, often quite brutal. The historian Tacitus quotes a barbarian chieftain from a conquered Germanic tribe: “They make a wilderness and call it peace.”

The Romans were great builders, constructing a vast system of roads, some of which are still in use, and an impressive network of aqueducts to carry water to a city that eventually housed about a million people. Culturally, they were no match for Greece. They did learn much from the Greeks, but only in some areas. In particular, as indicated in the Cicero quote above, they did not value higher mathematics. Certainly, their architects and engineers mastered practical mathematics, but the Romans produced no notable theoretical mathematics.

Greek culture did not disappear in the Roman era. The Latin language dominated only the western part of the Roman empire, while Greek remained the lingua franca¹ of the eastern Mediterranean. Furthermore, some Greek centers of learning, including Alexandria, continued their intellectual tradition, if at a somewhat reduced level of achievement.

Astronomy and Trigonometry

Astronomy has long been a stimulus for mathematics. In this period, it gave rise to a major area of math—trigonometry. The term comes from the Greek, trigon, meaning triangle, and metron, measure. The subject has developed beyond that in modem times, but early trigonometry was all about measuring triangles, that is, the sides and angles in a triangle.

Trigonometry is based on similarity of triangles. Consider a right triangle (Figure 1.28), where the angle ACB is a right angle. The ratio of the lengths of two corresponding sides will be the same in any triangle with the same angles. For example, suppose that in the triangle A′B′C′ the angle A′C′B′ is a right angle, and the angle α′ is the same as the angle α. Since the sum of the angles in a triangle is always the same, this means that the angles ABC and A′B′C′ are also equal; in other words, the two triangles are similar. Hence the ratios of corresponding sides will be equal.

Figure 1.28 Two similar right triangles.

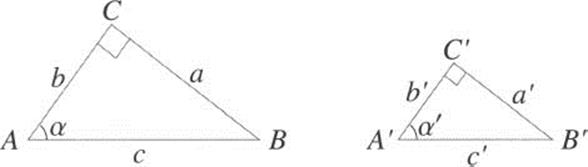
Consider the ratio a/c. Since the triangles are similar, a/c = a′/c′. In general, in any right triangle which also shares the angle α, the ratio of its corresponding sides will be the same number a/c. In trigonometry, we give that ratio a name: the sine of α, or sin α. Similarly, we name other ratios. The most common names are

The symbol cos is short for cosine, and tan is short for tangent. A convenient way to remember these is to rename the sides: a is called opp, because it is opposite the angle, b is adj, for adjacent, and c is hyp, for hypotenuse.

Why is this useful? It allows you to learn about an unknown triangle by studying a known similar triangle. Aristarchus used this idea, albeit not with the modem terms, to determine the ratio of the distances from the Earth to the Sun and Moon. First he measured the angle between the Sun and Moon when the Moon is half-full, a in Figure 1.29. (The diagram is not to scale.) He found it to be 87°. He also noted that, because the Moon is half-full, the Earth-Moon-Sun angle was a right angle. Then he used the argument above to deduce that the ratio of the distances to the Moon and the Sun, m/s, is cos 87° (m is adj, s is hyp). Finally, using various properties of triangles, he estimated that , so that . Therefore he concluded, the Sun is between 18 and 20 times as far away as the Moon.

Figure 1.29 Sun and Moon distances.

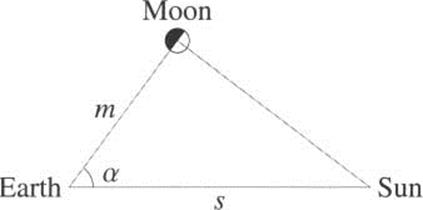
Aristarchus’ argument is perfect, but unfortunately his answer was off by a factor of about 20. The difficulty lay with the measurement; the angle is not 87° but about 89.8°. The small difference in angle makes a big difference in the cosine, because the angle is near 90°.

Aristarchus (c. 310–230 BCE)

Aristarchus was bom on the Greek island of Samos. He probably studied and worked in Alexandria, in the early 3rd century BCE. His only surviving work is On the Sizes and Distances of the Sun and Moon, from which the previous argument is taken. He also estimated the actual distances, not just their ratio, and from these the sizes of the Sun and Moon.

Aristarchus is most famous for being the first astronomer known to have posited that the Earth revolves about the Sun, and not vice versa. Other scholars of his day had a scientific problem with this, namely, if the Earth moves, why is it that the stars don’t appear to change during the year? His answer, that the stars are very far away, was not popular, although it has proven to be correct. Like Galileo 1900 years later, he was accused of impiety.

The most difficult part of Aristarchus’ argument, besides the measurement, was the approximation of cos 87°. Of course, he could have constructed a small triangle with the proper angles, and physically measured its sides. But, being a mathematician, he preferred more mathematical methods which held at the least the promise of greater accuracy. (He was actually quite accurate: cos 87° ≈ 1/19.1073.)

If astronomers were to use such arguments regularly, it would be useful to have tables giving values, say, of the cosine of every angle between 1 and 89 degrees. Then the astronomer need merely look up the answer, saving a lot of time. In fact, this is what happened. In order to study the heavens, they found such tables to be a great aid. In order to make these tables, however, they had to develop the mathematics of trigonometry.

The first mathematician known to have computed trigonometric tables was Hipparchus.

Hipparchus (c. 190–120 BCE)

Hipparchus was one of the greatest astronomers in history. He was bom in Nicaea, Bythnia (now Iznik, Turkey), where he made his first astronomical observations. Later on he moved to the Greek island of Rhodes in the Aegean Sea. Little else is known of his life.

Hipparchus wrote at least a dozen works, of which only one minor commentary survives. Most of what we know of his work comes from references in the texts of others, most notably Ptolemy.

Hipparchus’ work in astronomy built on earlier work by the Babylonians and Greeks, notably Eudoxus and Apollonius. Hipparchus made careful observations, and compiled a catalog of 850 stars. He estimated the distances to the Sun and Moon.

Much of mathematical astronomy in this period was dedicated to predicting the motions of the Sun, Moon, and planets. The word “planet,” which originally included the Sun and Moon, comes from the Greek planasthai, to wander, because planets wander against the unchanging background of the stars. It was this wandering that the astronomers wanted to model mathematically.

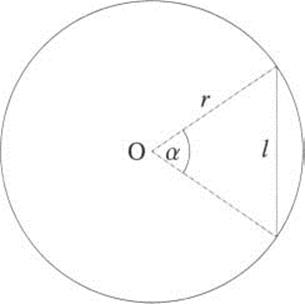
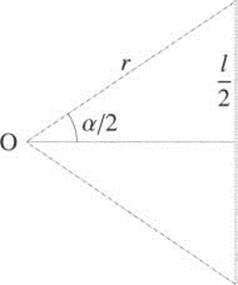
The details of the mathematical models used by Hipparchus are too involved to go into here, but basic to the mathematics was the understanding of triangles, both in the plane and on spheres. To assist in the computations, Hipparchus reportedly constructed a table of chords subtended by arcs of a circle of standard radius r. For example, the chord crda is the length l in Figure 1.30. Hipparchus computed approximations of crd α, for α a multiple of , up to 360°, a total of 48 (= 360/7.5) numbers. (He used a standard radius of 3438.)

Figure 1.30 Chord subtended by arc.

What, you might ask, has this to do with trigonometry? The answer can be found in Figure 1.31, which includes the triangle from the previous diagram, cut in half. Notice that . Since crd α = l, we have

So if we know the chord l, we know the sine, and vice versa.

Figure 1.31 Relation of chord to sine.

The greatest astronomical discovery of Hipparchus was the precession of the equinoxes. As the Earth revolves around the Sun, it also rotates on its axis, like a spinning top. The axis of this spin always points at the north star, Polaris, or so it seems. In fact, the Earth wobbles, so the axis points in different directions, completing a circle in about 26,000 years. So, in about 12,000 years, the north star will be Vega, not Polaris. (Actually, the axis will point about 5° from Vega, but close enough.) Since this change is so slow, it is no surprise that it took many centuries of observations to notice it. The way Hipparchus spotted it was by noticing that the location of the Sun against the background stars at the Spring and Fall equinoxes had changed, hence the name precession of the equinoxes.

The next major developments in trigonometry, over two hundred years after Hipparchus, were due to Menelaus.

Menelaus (c. 70–130 CE)

Mutually nothing is known of the life of Menelaus. He worked in Alexandria and in Rome. Only one of his works, Sphaerica, survives, in an Arabic translation.

Menelaus also made a table of chords. Although it has been lost, it was probably more extensive than that of Hipparchus, for it was in six books.

In the Sphaerica, Menelaus treats trigonometry as a science separate from astronomy. Most importantly, he deals with spherical trigonometry, triangles on a sphere, proving a number of results that were important to mathematical astronomy. Astronomers were interested in spherical trigonometry because they studied the celestial sphere. The mathematics of spherical triangles is different from that of flat triangles. For example, the sum of the angles of a spherical triangle is not always 180 degrees. In fact, it is not hard to construct spherical triangles where each of the three angles is 90 degrees, so that the sum is 270 degrees. (See the exercises.)

The apex of ancient trigonometric studies, as well as ancient astronomy, was in the work of Claudius Ptolemy.

Claudius Ptolemy (c. 100–178)

Little is known of the life of Ptolemy, the greatest of the ancient astronomers. He may have been bom in Egypt; he certainly worked at the Museum in Alexandria. Some of the astronomical observations he recorded can be dated to the period 124–142 in Alexandria.

Ptolemy wrote many works on science, mathematics, and astrology (yes), including two that were the standards in their fields for many centuries: the Geography, and his astronomical masterpiece, the Almagest.

Ptolemy’s Almagest is the astronomical equivalent of Euclid’s Elements. It was the culmination of Greek astronomy, not to be superseded until the work of Copernicus, Kepler, Galileo, and Newton. The book was originally called Mathematiki Syntaxis—Mathematical Collection. Later, it became known as Megisti Syntaxis—the greatest collection, and then in Arabic al-magisti, which morphed into the Almagest, by which it is commonly known today.

In the Almagest, Ptolemy gives a table of chords for all angles from one-half of a degree to 180 degrees, in intervals of one-half of a degree. The numbers, following the Greek astronomical tradition, are in the Babylonian sexagesimal notation.

In order to approximate these numbers, Ptolemy had to develop a variety of mathematical techniques. For example, using symmetry, it was easy to find the chords of 45° and 30°. Then Ptolemy demonstrated how, given chords for two angles, he could find the chord for the difference of those two angles. This allowed him to compute the chord of 15°. The formula Ptolemy discovered is equivalent to the following modem version.

The computations were not easy; it has been suggested that he employed (human) calculators to finish his table.

Given his table, Ptolemy could solve any triangles needed. He also applied these results to spherical trigonometry, using theorems of Menelaus and others, as well as his own. Finally, he presented a detailed mathematical model for each of the planets. The goal was to be able to predict their movements, e.g., to predict the time that Mars would rise on any given date, at any place on the Earth. In fact, he computed a number of such predictions, then compared them against actual observations to confirm the theory.

Ptolemy also produced another influential book, the Geography. In this work, Ptolemy listed 8000 locations, and drew a large map of the known world and twenty-six regional maps. There was a mathematical issue here: how does one represent the spherical Earth on a flat piece of paper? (Scholars were aware long before Columbus that the Earth was round. In fact, Eratosthenes had quite a good estimate of its radius in the 3rd century BCE.) Ptolemy came up with two solutions to this, two projections from a sphere to a plane. These were not improved upon for more than a thousand years.

Even though Ptolemy was aware of Eratosthenes’ work, he used an inferior (too small) estimate of the Earth’s size. Columbus used this size in the 15th century, one reason he thought he had reached Asia when he landed in the Americas.

The Silver Age of Hellenistic Mathematics

After the 3rd century BCE, the pace of mathematical research slowed. While there were advances, such as in trigonometry, much of the scholarly work was directed at preserving, not enhancing, mathematical knowledge.

There was a spurt of activity, however, from the middle of the 3rd century through the 4th century. In particular, works by Diophantus and Pappus stand out.

Diophantus (c. 210–290 CE)

About all that is known of Diophantus is that he worked in Alexandria in the 3rd century, and that he wrote the Arithmetica, in thirteen books.

A famous puzzle about him, written a couple hundred years after his death, asks for the number of years he lived.

“Here lies Diophantus,” the wonder behold. Through art algebraic, the stone tells how old: “God gave him his boyhood one-sixth of his life, One twelfth more as youth while whiskers grew rife; And then yet one-seventh ere marriage begun; In five years there came a bouncing new son. Alas, the dear child of master and sage after attaining half the measure of his father’s life chill fate took him. After consoling his fate by the science of numbers for four years, he ended his life.”

ANTHOLOGIA PALATINA

The Arithmetica is in thirteen books. We have versions of six books in Greek, from a 13th century copy. In the 1970s four of the other books were discovered in Arabic translations. These books are not arranged in the step-by-step logical fashion of Euclid’s Elements. Rather, they consist of a series of problems, 290 in the surviving books, more like the style of ancient Babylon or Egypt.

The Arithmetica is different from Euclid in another way; it has little geometry. The problems are about algebra and elementary number theory. This was apparently original with Diophantus. For this he has been called the “father of algebra.”

Here is one of the more elementary problems.

To divide a given number into two having a given difference.

Diophantus explained how to solve this for the case where the given number is 100 and the difference is 40. Before giving his solution, let us translate this into our modem notation. We are looking for numbers, say x and y, such that x + y = 100 and y – x = 40. From the second equation, we can solve for y, getting y = x + 40. Substituting this into the first equation, we get 2x + 40 = 100. This yields x = 30 and y = x + 40 = 70.

Diophantus solved this in a similar way, starting with: if x is the smaller number, then 2x + 40 = 100. His style was to state a general problem, then demonstrate a procedure for solving a particular case of the problem. He did not give a general solution, although his method could often be used to solve the general problem.

The problem above is called determinate: there are two equations in two unknowns, so there is only one solution. Most of Diophantus’ problems are indeterminate: there are more unknowns than equations, so there might be many solutions. For example:

To divide a given number into two squares.

The example he worked with had 16 as the given number. So the problem is to find two squares which sum to 16, that is, to solve x² + y² = 16. In these problems, Diophantus contented himself with finding a single solution, although again his method might serve to find others. He only accepted positive rational solutions. His methods were often ad hoc, and clever. In this case, the two numbers he found were and . (Check that they work!)

One of the most important innovations in the Arithmetica is the use of notation. Before this, algebraic problems were described entirely in words. This was called rhetorical algebra. Diophantus invented a system of notation that he used to make the solution of a problem easier. For example, he used for the variable name, what we would call x, and Δ^v for x². Thus, he would write Δ^vβ for 2x², since β, the second letter of the alphabet, was standard then for 2. Another example:

means the same as our 2x² + 3x, since γ is 3.

His system was not complete, so he needed to use some words still, in a style historians call syncopated algebra. Fully symbolic algebra didn’t arrive for another 1300 years.

The Arithmetica remained influential for many years, inspiring other mathematics well into the 17th century.

The other influential work from this period is the Synagoge, or Collection, of Pappus.

Pappus (c. 290–350)

Pappus was the most important geometer since Apollonius, some five hundred years earlier. Of the life of Pappus, we know only that he worked in Alexandria in the first half of the 4th century, and he had a son named Hermodorus. We know when he worked, because a solar eclipse that he observed can be dated to October 18, 320.

In addition to mathematics, Pappus wrote on astronomy, geography, and hydrostatics, but little survives of these works.

Pappus’ Collection is exactly that, a collection of separate books, written by Pappus, but perhaps put together by a student. The books are on different geometric topics, and of varying quality. Many of the books contain surveys of the work of his predecessors. In fact, the Collection is our best source for the lost works of many Greek geometers.

Book 5 concerns isoperimetric figures, those with different shapes but equal perimeters or surface areas. It contains a proof that, of all regular solids with the same surface area, the sphere has the largest volume. Concerning a similar problem in the plane, he has praise for honey bees, whose honeycombs are composed of hexagons.

Bees were endowed with a certain geometrical forethought… There being, then, three figures which of themselves can fill up the space round a point, viz. the triangle, the square and the hexagon, the bees have wisely selected for their structure that which contains the most angles, suspecting indeed that it could hold more honey than either of the other two.

Bees, then, know just this fact which is useful to them, that the hexagon is greater than the square and the triangle and will hold more honey for the same expenditure of material in constructing each. But we, claiming a greater share in wisdom than the bees, will investigate a somewhat wider problem, namely that, of all equilateral and equiangular plane figures having an equal perimeter, that which has the greater number of angles is always the greater, and the greatest of them all is the circle having its perimeter equal to them.

Book 7, “On the Domain of Analysis,” is the most influential. It discusses the “analytic” method Greek mathematicians used to solve problems or discover proofs, as opposed to the formal “synthetic” method of proof Euclid made famous. The latter is logically more rigorous but hides the actual discovery process. Book 7 also contains a number of theorems that were important in the development of projective geometry in the 17th century.

The Collection has been called the requiem for ancient Greek geometry. The next time geometry of this quality was developed was in the 17th century.

The Decline of Rome and the Rise of Christianity

Greek mathematics was dead by 500 CE. One is tempted to ask why it died, just as Edward Gibbon, in his The History of the Decline and Fall of the Roman Empire, famously asked why the Roman empire died. Perhaps the better question is why each, the empire and the mathematics, survived for so long. What was distinctive about the Roman empire was not that it ended, but that it was so successful for so long. Similarly, Greek mathematics is characterized by its long run of brilliance. So let us ask what sustained this brilliance.

An intellectual tradition usually requires a continuity of practitioners. It is not easy to pick up and read a copy of Euclid. Students then, as now, relied on an oral tradition to introduce them to the subtleties of mathematics. Hence the tradition might not survive the absence of mathematicians for a generation or two. The rise of larger institutions in which mathematicians could work was of considerable importance. Greek examples include the Pythagorean society, Plato’s Academy, and the Alexandrian Museum. Unlike now, however, the community of theoretical mathematicians in this period was never large, so it was susceptible to interruption.

The support of mathematics has, until recent times, always been rather tenuous. The cutting edge of theoretical mathematics is usually not very practical. Even though history has demonstrated many times that what begins as purely theoretical eventually develops practical applications, this connection is not always evident to those in power. Ancient mathematicians were heavily reliant on the patronage of the elite. They enjoyed this patronage in Greece before Alexander, and under the Ptolemies afterwards. As we have already seen, though, the Romans did not value mathematics highly, so their conquest of Egypt in the first century BCE was a blow to mathematics. Also notable in this conquest, in a skirmish between Julius Caesar’s army and local troops in 48 BCE, the library at the Alexandrian Museum was mostly destroyed by a fire. The Roman Marc Antony donated the library of Pergamum to Cleopatra as a replacement. It was stored at the nearby temple of Serapis.

Greek mathematics arose as part of a larger philosophical movement, in an attempt to find rational explanations for natural phenomena. The religious and philosophical climate underwent major changes in Roman times, which weakened this motivation. The most important change was the rise of Christianity, which had different philosophical priorities. Its ascendance was also accompanied by religious conflicts. It took some time for Christianity to become a major force, but by the 4th century it had risen to the status of official religion. This was a further blow to the Greek mathematical tradition.

As important as these cultural concerns were social conditions, which took a turn for the worse after 180 CE, when the emperor Marcus Aurelius died. What followed was a period of civil unrest, economic decline, and plague, especially in the western part of the empire. In the period 235–284 occurred what historians call the Crisis of the Third Century. During this time, dozens of men were declared emperor by some part of the Roman army, usually to die shortly thereafter. The constant civil unrest weakened the borders, so raids from the north and east became more frequent. A plague starting in 251 decimated the population in many places.

The empire stabilized again in the early 4th century, but in a quite different form. In particular, the emperor Constantine made two momentous changes: he converted to Christianity, and he moved the capital of the empire to the city of Byzantium, later renamed Constantinople (now called Istanbul). The western empire did not recover, however, continuing to suffer invasions from the north. Rome itself was sacked in 410 by the Visigoths. The traditional end of the western empire is usually dated to 476, when the German Odovacer deposed the western emperor Romulus (who was not recognized in Constantinople).

The eastern, Greek-speaking, part of the empire fared much better, with Constantinople remaining a major cultural and political center for many centuries.

Egypt’s Alexandria was not immune to the troubles of this time. Its economy suffered as trade declined. Support for mathematics also declined. In 391 a Christian mob attacked and destroyed the pagan temple of Serapis and much of its library, the one established in Cleopatra’s reign.

Theon (c. 335–405) and Hypatia (c. 355–415)

Theon was a mathematician and Neoplatonist who worked in Alexandria. He published work on astronomy and mathematics, as well as astrology. His most distinguished student was his daughter Hypatia, who became a leading scholar and teacher in her own right.

Hypatia is the most famous woman mathematician of antiquity. When she was sixty years old, on her way to a lecture, she was taken from her carriage by a mob, stripped, dragged to a neighboring church, and brutally murdered. She had become involved in a nasty political struggle and was accused of sorcery.

Theon wrote a number of commentaries on earlier works. The commentary was a popular form of scholarly writing for many centuries. The commentaries might include original research, or only exposition. Theon’s commentary on Ptolemy’s astronomical works Almagest and Handy Tables are mainly explanatory. Although a leading scholar of his day, it does not appear that he was a very original thinker.

Theon is most famous for his edition of Euclid’s Elements. This edition added little to the original, but replaced previous editions and became the standard for many years. In Western Europe, this was the source of all subsequent editions of Euclid until late in the 19th century.

Hypatia helped her father with his work and produced commentaries of her own. Our knowledge of her work is spotty, but it appears that she surpassed her father. She was certainly a famous teacher, offering instruction in philosophy and religious literature as well as mathematics and astronomy. Her edition of Archimedes’ Measurement of the Circle was the source of most subsequent editions.

Work at the Alexandrian Museum continued after the time of Hypatia, but did not produce any distinguished mathematics. In general, in the Greek-speaking eastern part of the empire, scholarship declined. In 529 the emperor Justinian ordered all pagan schools closed. The Academy in Athens was taken over by the state, and folded shortly thereafter. The memory of Greek mathematics did not die, however. We shall see later that Islamic mathematicians were able to learn from scholars trained in this tradition.

The story was different in the west, which suffered catastrophic decline. The population diminished. Rome in its heyday had about one million inhabitants; by the 8th century, no western city had more than about 50,000 people. Trade also declined precipitously. This was the heart of the Dark Ages.

Mathematics was still sometimes taught, usually in schools associated with Benedictine monasteries. There monks, often from Ireland, copied and preserved Greek and Latin manuscripts. The audience for these manuscripts was not large; literacy was not widespread even among the nobility.

The monks probably did not understand much of the mathematics. The most popular mathematics text was De Institutione Arithmetice of Boethius (480–524), which was based on the Introductio Arithmetica of the first century Alexandrian scholar Nicomachus. Although Nicomachus’ work was an elementary text at the time it was written, with no proofs, it was the most advanced arithmetic known in western Europe for many centuries.

Another influential handbook, by the Italian monk Flavius Magnus Aurelius Cassiodorus (c. 480–575), justified the study of arithmetic by quoting Jesus: “the very hairs of your head are all numbered.” In general, mathematical works from the time after Boethius often substituted the citing of authority for proofs. All but practical mathematics was gone from the West.

EXERCISES

The following table can be used in the exercises.

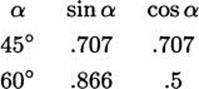
1.54 Consider the right triangle below.

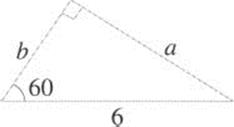
a) Find lengths a and b.

b) What is tan 60°?

1.55 Consider the right triangle below.

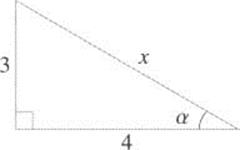
a) Find x.

b) Find tan α.

c) Find cos α.

1.56 Suppose that a right triangle has a hypotenuse of length 6, and the sine of one of its angles (other than the right angle) is .5. Find the lengths of the two legs.

1.57 If r = 100 and crd α = 75, what is sin(α/2)?

1.58 Suppose that a circle has r = 100. Find crd 90°.

1.59 Find sin 15°. (Hint: 15 = 60 – 45.)

1.60 Find sin 75°.

1.61 Find cos 15° and cos 75°.

1.62 Suppose that you have three points on the Earth, with A and B on the equator, a quarter of the way around the Earth, and C at the North Pole. What are the angles in the triangle ABC? (Hint: the angles don’t add up to 180°.)

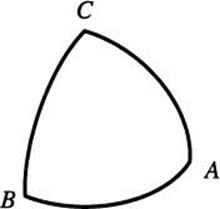
1.63 Geometry on the sphere is different from that in the plane. Try this exercise.

Hang your right arm down by your side. Curl your fingers into a fist, with your thumb pointing forward.

Lift your arm straight out away from your body, keeping your hand as it was, and not twisting your wrist.

Now move your arm so that it points forward. (Your thumb will point to the left.)

Finally, lower your arm straight down again.

Is your thumb now pointing the same direction it was at the start? What does this have to do with a sphere? (Hint: a sphere is the set of points at the same distance, say arm’s length, from a center, say a shoulder.)

1.64 According to the puzzle in the text, how long did Diophantus live? (Hint: the age seems to be divisible by 7 and 12.)

1.65 How might Diophantus have written 3x² + 2x?

1.66 Use Diophantus’ method to find the general solution of the first Diophantus problem, that is, to find x and y such that x + y = s and y – x = d, for any sum s and difference d.

1.67 Another problem Diophantus considered is this: to find a square number between 5/4 and 2. Find such a number. (Recall that Diophantus only allowed positive rational numbers.)

¹From “Earth at Night.” C. Mayhew and R. Simmon (NASA/GSFC), NOAA/NGDC, DMSP Digital Archive.

¹Circa (abbreviation c.), from the Latin, means “around.” We will use it for approximate dates. BCE (Before Current Era) is becoming standard for dates before the year 0, what used to be written B.C. CE is used for dates after the year 0, in place of A.D.

¹From “Earth at Night.” C. Mayhew and R. Simmon (NASA/GSFC), NOAA/NGDC, DMSP Digital Archive.

¹Map by Sémhur. Wikipedia Commons.

¹From “The Blue Marble.” R. Stöckli, R. Simmon. (NASA/GSFC) http://visibleearth.nasa.gov/.

¹Diagram by Pbroksl3. Wikipedia Commons.

¹From the Italian, literally “Frankish language,” lingua franca refers to a common language used to communicate by people with different native tongues. For example, English is now the lingua franca of the scientific community.