Mathematics for the liberal arts (2013)

Part I. MATHEMATICS IN HISTORY

Chapter 2. THE GROWTH OF MATHEMATICS TO 1600

2.2 India

India.¹

India to 1600.

History to 1600: An Overview

The Indian tectonic plate began crashing into Asia about 55 million years ago, a collision that continues, deforming both India and Asia. Major results of the collision are the Himalayan Mountains, the tallest in the world, and the Tibetan Plateau, with an area about half that of the continental United States and an average height above that of the highest peak in the lower 48 states. Most of the major rivers in Asia originate in either the Himalayans or the Tibetan Plateau, including China’s Yellow and Yangtze rivers.

The rivers that dominate Pakistan and northern India are the Indus and the Ganges. (Though separate countries now, India and Pakistan have not always been so. For the purposes of this section, we will refer to the whole area as India.) The Indus rises in Tibet and flows through China and Pakistan into the Arabian Sea, west of India. The Ganges rises in India and flows through northern India into Bangladesh, to empty into the Bay of Bengal to the east of India. Much of northern India lies in the Ganges plain.

By 3000 BCE agriculture had come to the Indus River valley, influenced by the Sumerians. The staples were wheat and barley. By 2500 BCE there was a flourishing civilization in modern-day Pakistan and western India, called the Harappan civilization. This urban civilization is known primarily through excavations of two of its cities: Mohenjo-daro and Harappa. Even though the Harappan civilization covered an area larger than the ancient civilizations of Mesopotamia, Egypt, or China, less is known of it. Virtually nothing was known until the excavations of Mohenjo-daro and Harappa began in 1920. Its script has still not been deciphered.

About 1500 BCE the Indus River valley was invaded by Aryans from central Asia. Their military power was based on chariots. The subsequent civilization is usually called Vedic, after the vedas, which were early Hindu religious works. This was the time that Hinduism, and the caste system with its rigid social strata, were developed. The language of the Aryans was Sanskrit, from which most current Indian languages derive. Sanskrit is in a family of languages called Indo-European, which contains almost all modem European languages. Indeed, it was the similarity of Sanskrit to classical Greek and Latin that inspired the British Chief Justice of India, Sir William Jones, to invent historical comparative linguistics in 1786. From roughly 800–300 BCE, the Aryans extended their domain throughout the Ganges River basin in northern India. In the 6th century, Siddhartha Gautama, Buddha, was bom in modern-day Nepal.

In 326 BCE Alexander the Great invaded India. He conquered most of the Indus River valley by the following year, then headed back west. After his death, one of his generals established the Seleucid dynasty, which ruled much of western Asia. Then Chandragupta Maurya, starting in eastern India, established the Mauryan empire (317–184 BCE), the first to unify virtually all of India. Eventually, he ruled both the Ganges and the Indus River valleys. Chandragupta’s grandson Ashoka extended the empire from Afghanistan to Bangladesh, from Nepal almost to the southern tip of India. Ashoka is one of the most famous figures in Indian history. Early in his reign, he was known to be quite ruthless. However, in his conquest of Kalinga (modem Orissa) in eastern India, he witnessed such destruction and suffering that he experienced a change of heart. He renounced conquest thereafter, converted to Buddhism, and spent much of the rest of his life promoting it.

After the Mauryan empire, India was divided into a collection of smaller states. The next great empire was the Gupta dynasty (320–535 CE), founded by another Chandragupta. This was a brilliant period in Indian culture, including literature, music, architecture, and art. The Shakespeare of Sanskrit drama, Kalidasa, flourished around the year 500. Indian culture was spread by merchants and missionaries throughout southeast Asia, as far as Indonesia. This time is also known as the golden age of Indian science, particularly in astronomy and mathematics.

The Gupta dynasty was overthrown in 535 by the White Huns, called the Rajputs. There followed another period of smaller states. In 711 the lower Indus valley was conquered by the Muslims. Later, Muslim rulers conquered virtually all of India; notable is the Delhi Sultanate period (1206–1526), when India was ruled by a succession of Muslim dynasties.

Early Indian Mathematics

Indian numerals were decimal, grouped by tens. Eventually, Indian mathematicians developed the number system that we use today, but early on their system was not positional; they did not only have nine or ten symbols whose interpretation was based on their position. In addition to the symbols for 1,…, 9, they had separate symbols for 10, 20, and so on.

Much of our knowledge of early Indian mathematics comes from Śulbastras written between 800 and 200 BCE. These were a type of poem called a sutra. The Śulbastras contained compact instructions for building altars for sacrifices. They had formulas (written in words, not symbols) for a variety of areas and volumes, some accurate, some not. There was no notion of proof. These poems did reveal a knowledge of basic geometry, including the Pythagorean Theorem; one had an approximation of the square root of 2 accurate to five decimal places.

India was sufficiently close to Mesopotamia and the Mediterranean to at least occasionally exchange mathematical ideas. There is evidence of an influx of Mesopotamian astronomy around 600 BCE. When Alexander invaded in 326 BCE, he brought with him not only soldiers, but also scholars. There were other transmissions of knowledge, especially astronomy. Native Indian astronomy and mathematics were inferior to the imports until the time of the Gupta empire.

Indian mathematicians.

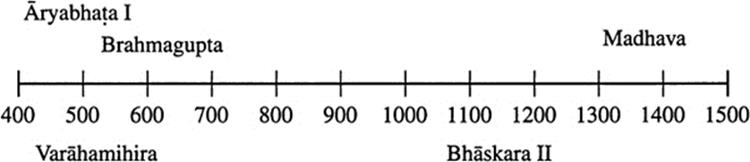
The Golden Age

During the Gupta empire, northern India was one of the richest and most brilliant civilizations in the world. The capital of the empire was at Pataliputra, a city on the Ganges in eastern India, near modern-day Patna. The Gupta kings supported learning, founding the great Nalanda University, near Pataliputra, which was one of the world’s major centers of learning until it was sacked and burned in 1193.

Indian mathematics of this time was developed mainly in service to astronomy. Indian astronomy was based on Greek models. The Indian tradition was concentrated in schools called paksas, of which the most famous were the Brahmapaksa in Ujjain in central India, and the ryapaksa in Kusamapura in northern India.

I (476–550)

The first Indian mathematician of whom we have any knowledge is I. He lived in Kusamapura, near Ptaliputra, where he founded the ryapaksa school of astronomy.

Although he wrote at least two texts, only one, the , survives. The was written in verse couplets, and was completed when the author was twenty-three years old. It is one of the most influential astronomical works in history, not only in India but subsequently in the Muslim world.

The first Indian satellite, launched in 1975 (on a Russian rocket), was named Aryabhata in his honor.

Although the was primarily an astronomical text, a sizable portion of it, 33 out of 118 verses, deals with mathematics. It has trigonometric tables to be used in computation, and a good approximation to π, namely, 3.1416.

also gave formulas for the sum of squares and cubes, in modem notation:

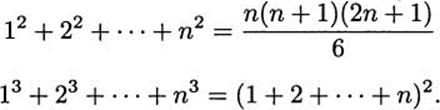
The contained a novel method for solving certain types of indeterminate equations. Using the notation introduced in the section on China, we can write the problem as follows: given numbers a, b, r, s, find a number N such that N ≡ a (mod r) and N ≡ b (mod s). This is a special case of the Chinese Remainder Theorem. As in China, such problems arose in astronomical calculations.

There are no proofs in the .

Varhamihira (505–587)

Varhamihira was a leading astronomer of the Brahmapaksa school, working in Ujjain. His major work is the Pancha-siddhantika (Five Treatises). This work summarizes the astronomical knowledge of his time, including much western (Babylonian, Egyptian, Greek) astronomy, as well as native Indian astronomy.

Varhamihira was also interested in astrology, about which he wrote extensively.

The Pancha-siddhantika improved on the trigonometric tables given in the . In addition, Varahamihira discovered a number of trigonometric identities, given below in modem notation.

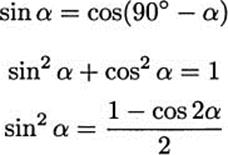
The word identity means that each equation holds for every value of α. For example, if we know that cos 60° = .5, then the first identity tells us that sin 30° = .5.

In another work, the Brihat Samhita, Varahamihira dealt with combinatorics. Among the many topics in the book, he gave formulas for making various perfumes. One question he addressed was how many perfumes could be mixed using a choice of four ingredients from a total of 16: “If a quantity of 16 substances is varied in four different ways, the result will be 1820.” He did not tell us how he arrived at that number, but it seems likely that he had a procedure equivalent to the following formula. The number of ways to choose r items from a total of n (these are called combinations) is

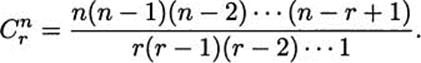
In his example,

Brahmagupta (598–c. 665)

Brahmagupta lived most of his life in Bhillamala, modern-day Bhinmal, in Rajasthan in northwestern India. He belonged to the Brahmapaksa school, and headed the astronomical observatory in Ujjain. He produced four texts on astronomy and mathematics, of which the most famous is the Brhmasphuasiddhnta (Correct Astronomical System of Brahma). This text, written in 628, was translated into Arabic in Baghdad in 771, where it had a major influence on Islamic astronomy and mathematics.

Brahmagupta, unlike many mathematicians until quite recently, was comfortable dealing with negative numbers. He gave correct rules for doing arithmetic on negative numbers; for example, a negative times a negative equals a positive. He was one of the first to deal with 0 as a number, although he thought that one could get away with dividing by 0, which modem mathematics disallows because it leads to logical inconsistencies.

Brahmagupta also studied Diophantine equations, indeterminate equations with integer solutions. An example is the equation 2x + 3y = 17, where x and y must be integers. There are many solutions; two of them are x = 1, y = 5 and x = 4, y = 3. Diophantus had studied these as well (hence the name), but only gave one solution per equation. Brahmagupta completely solved the linear Diophantine equation ax + by = c, where a, b, and c are given integers. More on linear Diophantine equations can be found in Sections 5.9 and 5.10.

Another equation that Brahmagupta studied was of the form y² = ax² + b, where a and b are given integers. The case where b = 1 is now called the Pell equation.

A simple example of a Pell equation is y² = 2x² + 1. It is easy to find one solution, x = 2, y = 3, which we will write (2,3). Brahmagupta gave a novel method for generating new solutions from old. First, he wrote two solutions, one above the other. See Figure 2.5, where we use the solution (2,3) twice.

Figure 2.5 Generating a new solution to y² = 2x² + 1.

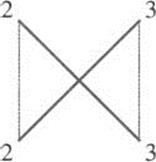
Then he generated a new solution by doing crosswise multiplication to get a new x, namely, x = 2 · 3 + 2 · 3 = 12, and vertical multiplication (doubling the first product) to get a new y, namely, y = 2(2 · 2) + 3 · 3 = 17. Thus we have a new solution, (12, 17). Let’s check: 2 · 12² + 1 = 289 = 17². In general, if we start with two (possibly identical) solutions of the equation, this crosswise and vertical multiplication will produce a new one. As another example, let us start with (2, 3) and (12, 17) (Figure 2.6). The generated values are x = 2 · 17 + 12 · 3 = 70 and y = 2(2 · 12) + 3 · 17 = 99. Our new solution is (70,99). Check!

Figure 2.6 Generating a third solution to y² = 2x² + 1.

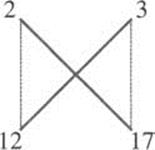
European mathematicians did not achieve Brahmagupta’s level of understanding of the Pell equation until the 18th century, more than one thousand years later.

In geometry, Brahmagupta found a formula for the area of a cyclic quadrilateral, which is a quadrilateral that can be inscribed in a circle. Using the notation of Figure 2.7,

where s is one-half of the perimeter: .

Figure 2.7 A cyclic quadrilateral.

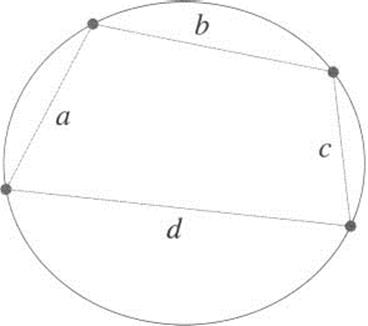
If we let d = 0, then we have a triangle, which can always be inscribed in a circle, and the formula reduces to the famous Heron’s formula for the area of a triangle: A = . (Heron was a Greek scholar who worked in Alexandria in the first century CE. He is most famous as an engineer and inventor.)

Notation and Computation

Perhaps India’s most important contribution to mathematics is our modem decimal place-value system, with 0. This system developed gradually. By around 600 CE a place-value system was employed, using only nine symbols (corresponding to our digits 1, …, 9). The use of 0 may have come a bit later, but was probably in place by the early 8th century. This system spread to the Arab world, and later to Europe. It is now usually called the Hindu-Arabic system.

The symbols we use for the digits are not the same as the original Hindu ones, although there is some overlap. The symbols themselves evolved as the system passed from India to the Arab world to Europe, being given their modem form by Albrecht Dürer in the early 16th century.

The Indians did not use decimals for fractions; this was introduced later in the Muslim world.

The great value of this numerical system was how easy it made computation. The Indians themselves developed a method of multiplying numbers, later called gelosia, or lattice, multiplication. (Gelosia was a type of iron grill placed over windows in medieval Italy.) Here is an example, computing 425 × 629. First, we draw a 3 × 3 grid (because each of the numbers has three digits), then place the two numbers above and to the right of the grid (see Figure 2.8).

Figure 2.8 Gelosia multiplication: 425 × 629.

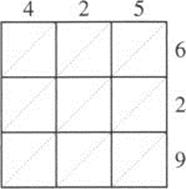
Next, multiply each of the digits of the first number by each one of the second number, placing the result in the associated grid square. For example, since 4 × 6 = 24, we place a 2 and a 4 in the top left square, the 2 above the diagonal, the 4 below. This gives us the left diagram in Figure 2.9. If there is only one digit in the product, place it below the diagonal. Doing this for all digits gives us the right diagram in Figure 2.9.

Figure 2.9 Gelosia multiplication: placing products inside the squares.

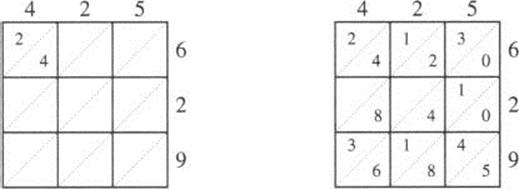
Now we look at the diagonals. Beginning at the lower right, we add the numbers in each diagonal, writing the sum below the grid. If the sum is more than 9, we carry the tens digit to the next diagonal. The first three steps in this process are shown in Figure 2.10.

Figure 2.10 Gelosia multiplication: summing the diagonals.

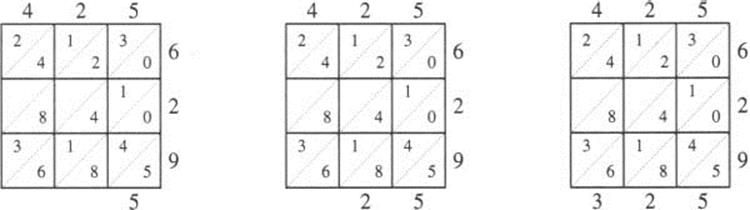
We continue summing the diagonals, writing the rest of the digits up the left side of the grid (Figure 2.11). We can then read the answer, starting down the left side and across the bottom: 425 × 629 = 267, 325.

Figure 2.11 Gelosia multiplication: 425 × 629 = 267,325.

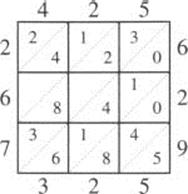
This method of multiplication spread from India to the Arab world, and then to Italy, introduced by Fibonacci in 1200. It was widely used in Europe until the 17th century. Printing may have helped lead to its demise, since the diagrams were not easy to typeset.

Medieval Indian Mathematics

Bhskara II(1114–1185)

Bhaskara II was perhaps the greatest medieval Indian mathematician. (Bhaskara I was a 7th century astronomer/mathematician.) The son of a noted astrologer, Bhaskara II headed the astronomical observatory in Ujjain. He was thus a successor to Varahamihira and Brahmagupta, and the last great scholar of the Brahmapaksa.

Bhaskara wrote at least a half-dozen works; the most influential are the Siddhanta Siromani (Head Jewel of an Astronomical System), Lilavati (The Beautiful), and Bijaganita (Seed Counting or Root Extraction). The latter two are sometimes considered part of the first text.

Bhaskara produced improved trigonometric tables and, more than most of his predecessors, explained the theory behind the computations. He states the equivalent to the following trigonometric identities.

It is possible that Bhaskara’s work was influenced by Islamic astronomy, which was very sophisticated at this time.

Bhaskara is also notable for his use of algebraic symbols. For example, he used the initial syllables for various colors where we would use the symbols x, y, or z.

The highlight of Bhaskara’s mathematical work was his study of indeterminate equations of the form y² = Dx² ± b, where D and b are given positive integers. Extending Brahmagupta’s earlier work, he wrote down a general method for solving the Pell equation y² = Dx² + 1, although he did not give a proof that it always worked. (The first such proof didn’t appear until 1929.)

After the time of Bhaskara II, northern India entered a turbulent period with the invasion of Islamic armies, and scholarship suffered. On the southwest coast of India, however, a cultural center flourished at Kerala, sheltered by mountains to its east. Its leader was Madhava.

Madhava (1340–1425)

Madhava of Sangamagramma was bom in a town near Cochin, Kerala. He worked on both astronomy and mathematics. Some of his astronomical works have survived, but we know of his mathematics only through commentaries of his successors.

The most important mathematics developed in Kerala originated in attempts to improve the accuracy of trigonometric tables, which were used in astronomy and navigation. The issue addressed was how to obtain accurate approximations to trigonometric values. Below, we present in modem notation what Madhava discovered.

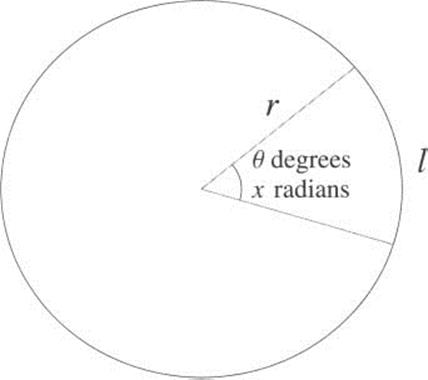
First, we make a convenient change of unit. Instead of using degrees, we measure angles in radians. Instead of 360 degrees to a circle, we have 27r radians per circle. The conversion is easy:

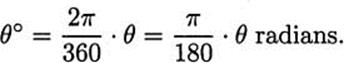
So, for example, 90° is radians. One advantage of this unit is in figuring the length of an arc of a circle, for example l in Figure 2.12. Recall that the circumference of a circle is 2πr, where r is the radius. Using 360 degrees to a circle, the length of the arc of θ degrees is then . In a similar way, if we use radians, we have 2π radians to a circle, so an arc of x radians has length , a simple formula.

Madhava discovered that polynomials can give good approximations of some trigonometric functions. For example, if x is small, then sin x ≈ x. (The symbol ≈ means “approximately equal to.”) A better approximation can be obtained by using a third degree polynomial: sin x ≈ x – x³/6. This can be continued, getting better and better approximations by using higher degree polynomials. Of course, we can’t use just any polynomials. Madhava found the pattern required for the polynomials. Here are the first four.

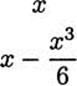
Figure 2.12 The length of a circular arc.

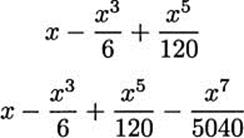
Part of this pattern should be clear; each term has odd degree, and we alternate adding and subtracting terms. But where do the denominators come from? It turns out that they are factorials. A factorial is defined, for any positive integer, as the product of the integers up to and including that one. For example, 5! = 5 · 4 · 3 · 2 · 1 = 120. Using this notation, we can write the four polynomials above in this way.

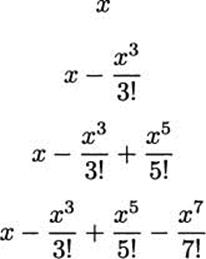
For small values of x, these give good approximations to sin x. If you continue this process, these numbers, for any real number x, get as close as you like to sin x. We write this as follows.

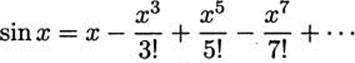
Who would have thought that trigonometric values would be so closely related to polynomials?

There is a similar pattern for the cosine. In this case,

The expressions on the right are called power series expansions of the functions.

The tangent function has a series expansion too. (Recall that the tangent is the sine divided by the cosine.) First, let us introduce something called an arctangent. For a number x, the arctangent of x, abbreviated arctan x, is defined by

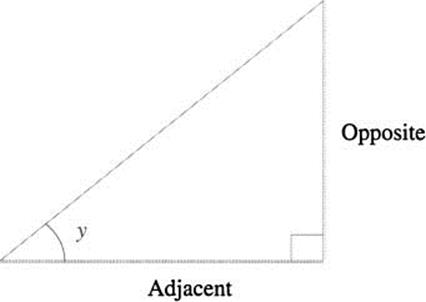
In other words, the arctangent of x is the angle whose tangent is x. As an example, let us compute y = arctan 1, so that tan y = 1. Recall the formula for the tangent in the triangle: opposite over adjacent. (See Figure 2.13.) If tan y = 1, then opposite equals adjacent, so by symmetry the angle is 45°, which in radians is 45 · (π/180) = π/4. Hence arctan 1 = π/4.

Figure 2.13 tan y = opp/adj

Madhava obtained a power series expansion for the arctangent. In modem terms, we can write it thus:

Let us apply this to π/4 = arctan 1:

This amazing formula for π was rediscovered by Gottfried Leibniz in the 17th century, when it became deservedly famous. But Madhava had it first.

Historians of mathematics have only studied Kerala fairly recently, so our knowledge is not complete. In particular, little is known of the possible transfer of knowledge to and from Kerala. Kerala played a major part in the spice trade between the East Indies and the West. In his historic voyage of exploration, the first place in India where the Portuguese explorer Vasco Da Gama landed was at Kappad in Kerala, on May 27, 1498. It is possible that the mathematical discoveries of Kerala made their way to Europe. Certainly, trigonometric power series played an important part in the development of calculus in the 17th century. It is intriguing to think that India may have contributed to this great advance in mathematics.

EXERCISES

2.16 Find l² + 2² + · · · + 100² and 1³ + 2³ + · · · + 100³.

2.17 How many perfumes could be mixed using a choice of three ingredients from a total of twelve?

2.18 A poker hand is a set of five cards chosen from a deck of 52 cards. How many poker hands are there?

2.19 Two solutions to the Diophantine equation 2x + 3y = 17 are given in the text. Find two more solutions. (Hint: either use trial and error or look for a pattern.)

2.20 Show that 2x + 4y = 101 has no integer solutions. (Hint: is 2x + 4y odd or even?)

2.21 Two solutions to the Pell equation y² = 2x² + 1 are given in the text. Use Brahmagupta’s method to find another solution.

2.22 Find four solutions of the Pell equation y² = 6x² + 1.

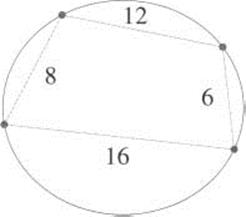
2.23 Find the area of the cyclic quadrilateral shown below.

2.24 Find the area of the triangle whose sides have lengths 1, 2, and 3.

2.25 Use Gelosia multiplication to compute.

a) 726 × 512

b) 2247 × 52

2.26 Use Varahamihira’s trigonometric identities and the table to compute.

a) sin 60°

b) sin 45°

c) sin 15°

d) sin 75° (Hint: 75 = 45 + 30.)

2.27 Use the definitions of the sine of an angle as opposite over hypotenuse and the cosine as adjacent over hypotenuse to prove Varahamihira’s identity sin² α + cos² α = 1. (Hint: use the Pythagorean Theorem.)

2.28 Find the radian measure of each angle.

a) 60°

b) 45°

c) 15°

d) 720°

2.29 Find the degree measure of each angle.

a) π/6 radians

b) 27π radians

c) 5 radians

d) 360 radians

2.30 What is arctan 0? (Hint: sin 0 = 0.)

2.31 Use the first three terms of the power series expansion to approximate.

a) sin .5

b) cos.5

c) arctan .5