Numbers: Their Tales, Types, and Treasures.

Chapter 11: Numbers and Philosophy

11.9.MATHEMATICAL MODELS

A mathematical model is a representation of a typical real-world situation, expressed in the language of mathematics. It is usually created to solve a problem, or to answer some question. Depending on the scope of the model, the mathematical representation could be an entire field of mathematics (for example, the axioms, definitions, and theorems of Euclidean geometry) or just a mathematical equation. The process of translating the real-world situation into the mathematical model is fittingly called mathematization (see figure 11.4).

As an example of a real-world situation, consider the weather in some region of the world. We could ask, for example, “What is the weather going to be tomorrow?” Translating this question into mathematical language is by no means simple. The mathematical model needed for a weather forecast can be derived from the physical laws that govern the temporal change, and the mutual influence of physical variables related to weather phenomena, like wind velocity, air pressure, temperature, and humidity. The physical laws typically lead to a mathematically rather complicated system of differential equations. The question about tomorrow's weather would then translate into a question about the solutions of these equations. One would then try to solve these equations by a numerical computation, which uses as input a collection of initial data describing today's weather (temperature, wind velocity, etc., measured at various locations of the country) and which takes into account boundary conditions describing the local geography (mountains, coastline, etc.).

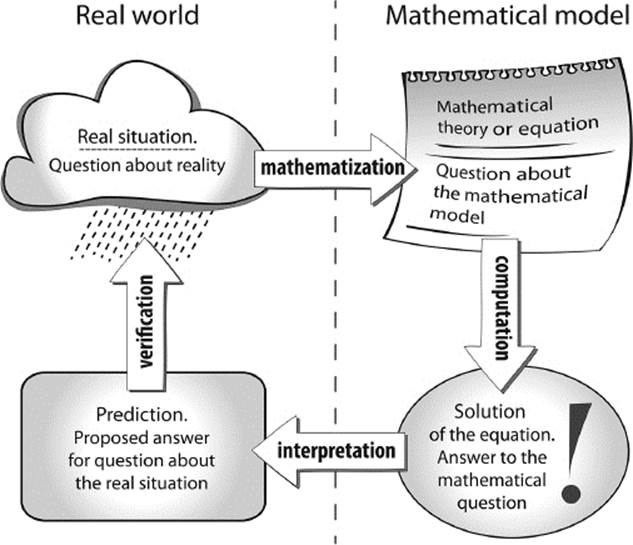
Figure 11.4: Applications of mathematics—the modeling cycle.

Once we have obtained a mathematical answer within the model, how can we know that the mathematical result is true? The answer is we can never be sure. In a complicated model, there are many sources of possible errors. In order to make weather forecasts feasible within a reasonable time allowed for the computation, the model usually contains simplifications and approximations, and, moreover, the initial state that defines the starting point of the computation is only known with limited accuracy.

One, therefore, has to test the model and examine its validity by comparing the outcome of the mathematical computation with observations in reality. In order to do this, one first has to interpret the result of the mathematical computation in terms of the real-world situation at hand. The mathematical expressions (the solutions of the model equations) have to be translated into tomorrow's values of the physical variables related to weather phenomena. From these values, a meteorologist can conclude tomorrow's weather conditions. The interpreted result is, thus, a prediction about an observation concerning physical reality. The comparison of the prediction with the actual situation (called validation, or verification) will either confirm the model or reveal a flaw. Whenever the prediction disagrees with the observation, we will have to adjust and improve the model. This can be done, for example, by taking into account more details, or by correcting any error that might have occurred in the whole process.

Natural numbers and their arithmetic can likewise be interpreted as a mathematical model of certain aspects of reality. We are just not accustomed to think that way, because natural numbers and arithmetic are so fundamental and are applied as a matter of course. And yet, the process of modeling certain phenomena with numbers and arithmetic has the same structure as in the case of weather forecasting.

In the example depicted in figure 11.5, the real-world situation is about combining sets of discrete objects. If we put first five and then three apples into a basket, how many apples would be in the basket? The answer is so obvious that we are usually not aware that we in fact used a mathematical model—natural numbers and their addition. The mathematical representation of this situation involves just two natural numbers, 5 and 3, and the question about the real-world situation can be translated into the mathematical question, “What is the result of 5 + 3?”

As always, the mathematical model may lack some details—in this case, the model completely disregards the concrete nature of the objects and just describes their numbers. A model need not have more details than necessary to answer the question at hand. So the mathematical question is just about numbers, not about the geometrical shape or the arrangement of the apples. The next step is computation, and, unlike the computations involved in a weather forecast step, it does not require a computer to produce the result “8.” Next, the result has to be interpreted in view of the real situation. We remember that we wanted to know the number of apples in a basket and made the prediction that it would contain eight objects. The final step would be a reality check (validation, verification) in order to compare the outcome of the mental operation with the real situation. Here, this is simply done by counting the number of apples in the basket.

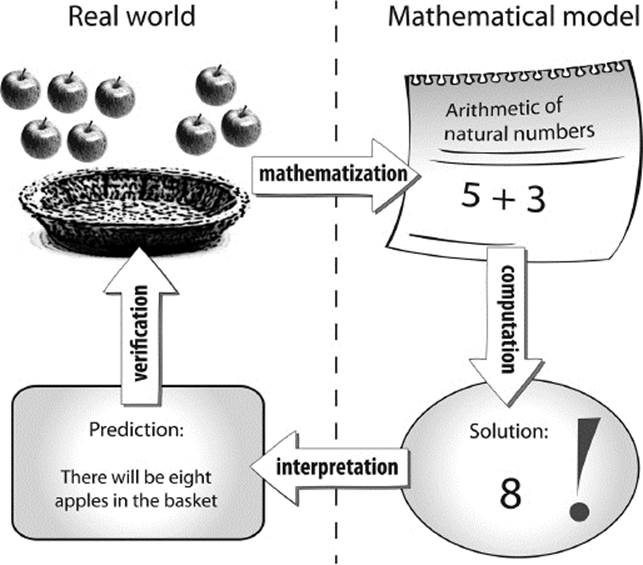
Figure 11.5: Arithmetic of numbers as a model.

If a model makes valid predictions in many concrete cases, if it already has been applied and tested successfully in many situations, we have some right to trust in that model. By now, we believe in the model “natural numbers and their arithmetic” and in its predictions without having to check it every time. We do not expect that the result might be wrong; hence the verification step is not needed any longer for validating the model. If the model had a flaw, it would have been eliminated already in the past. We trust the model so much that if the basket contained only seven apples, we would not look for an error in the model but instead would look for the thief who stole the apple.

But we also have to know that every model has its limitations. The model of natural numbers and their sums is very successful to determine the number of objects in the union of two different groups of well-distinguished objects. But as a mathematical model, the arithmetic of numbers is not generally true but only validated and confirmed for certain well-controlled situations.

In some situations, the arithmetic of numbers does not give the appropriate answer. For example, if you put together 5 cm³ of water and 3 cm³ of salt, you would not obtain 8 cm³. The mixture would have a smaller volume than 8 cm³ because a large part of the salt would dissolve in the water and the solution is denser than pure water, thus occupying less space.

Assume you walk forward at the rate of 3 miles per hour on a ship that moves with a speed of 5 miles per hour with respect to the coast. How fast would you be moving with respect to the coast? Addition of natural numbers is also a good model for this situation, and the answer would be that you would be moving at the rate of 8 miles per hour with respect to the shore. But this answer is only approximately true. For the addition of velocities, it would be more accurate to use the relativistic addition of velocities. According to this model, your velocity, as seen from the coast, would be less than 8 miles per hour. It would be 7.99999999999999973…miles per hour.

The error is so small that it was unknown before 1905, when Albert Einstein set up the special theory of relativity. According to this theory, velocities cannot be added in the usual way, as you would add apples. Instead one has to use the following formula to determine the sum of a velocity u and a velocity v: If the velocity of the ship with respect to earth is v and you move in the same direction with velocity u with respect to the ship, then your velocity with respect to earth would be not simply u + v, but rather

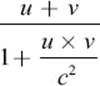
Here c represents the velocity of light, which is 670,616,629 miles per hour (its exact value is 299,792,458 meters per second). Because the speed of light is so large, the fraction is extremely small, and so the denominator is very close to 1 in all situations of everyday life, and one can usually neglect it. But the denominator inhibits any relative velocities greater than or equal to c. For example, if you added the velocities and , you would not get c, but only .