Numbers: Their Tales, Types, and Treasures.

Chapter 3: Numbers in History

3.1.NUMBERS IN BABYLON—THE FIRST PLACE-VALUE SYSTEM IN HISTORY

The first highly developed culture was in the land of Sumer, in southern Mesopotamia (today's Iraq). The first towns and cities there were built by the Sumerians more than five thousand years ago, and it was there that the earliest known writing in history appeared. It was probably developed to organize economic processes and record them in durable form. Also, writing was needed to facilitate administration that had become very complex, so that human memory alone became insufficient. The cuneiform script was developed from the first versions of writing using pictographic symbols. In the often-flooded areas between the Euphrates and Tigris rivers, there was plenty of clay available, and the Sumerians formed clay tablets, engraving symbols with a wedge-shaped tool in the still-soft clay. The name cuneiform means, in fact, “wedge-shaped” (Latin cuneus, or “wedge”). Gradually, the number of different symbols was reduced, and the cuneiform writing became less pictographic and more and more phonological, with symbols describing the sounds and syllables of the spoken language. When the Akkadians conquered Sumer in about 2300 BCE, the two cultures merged, and the Sumerian writing system came into use everywhere in Mesopotamia, where the Babylonian empire soon emerged. From the innumerable clay tablets that were created by Sumerians, Akkadians, and Babylonians, at least half a million tablets have survived until today. Among them, about four hundred have mathematical content or deal with mathematical problems. It is from these clay tablets that we know about Babylonian science.

It is most interesting that the Sumerians and the later cultures in Mesopotamia used a sexagesimal numeral system, which means that the base of the numeral system was 60, rather than the base-10 that we are all quite accustomed to in our daily lives. It is the only culture of the world where such a large base number was chosen.

It has been speculated that the reason for the use of a base-60 system was due to astronomy and astrology. Babylonian priests observed the precise locations of the planets, the moon, and the sun on the celestial sphere. The location of the sun with respect to the stars can be determined during the short period before sunrise, when the brightest stars are still visible. They found that the sun moves in the firmament along a great circle, the ecliptic, in roughly 360 days. This would be the origin of dividing a complete circle into 360 degrees. A circle is easily divided into six parts, each of which is 60 degrees, by marking off the radius length along the circumference (as in the construction of the hexagon). Sixty days roughly corresponds to two lunar periods and has some other nice properties as a unit—for example, it can easily be divided into 2, 3, 4, 5, and 6 parts. Therefore, it was chosen as the base of their number system.

This explanation might be appealing, but it has the disadvantage of being most probably wrong. As Georges Ifrah, in his book The Universal History of Numbers, has noted, it presupposes that a highly developed science like astronomy was available before the development of a number system.¹ However, a number system fulfills some very basic needs of an emerging culture, and all historic evidence indicates that a number system would be much older than any systematic observation of the sky. Also, a numeral system is not chosen according to sophisticated and abstract mathematical considerations, such as the number of divisors. People get accustomed to a grouping scheme by systematic use and cultural habit, in a phase of development that precedes any advanced knowledge of numbers. Ifrah hypothesizes that the Sumerian sexagesimal system had developed when two prehistoric groups of people merged, one accustomed to a quinary system (base-5), the other with a duodecimal system (base-12). As discussed in the first chapter, such a combination of base-12 and base-5 can be easily realized when counting with fingers. Pointing with the thumb of the right hand to the phalanges of the four opposing fingers lets you count to 12. Counting the groups of 12 with the five fingers on the left hand would give 60 as a natural unit that can be counted with the fingers of both hands and can be understood by people accustomed to base-5 as well as by people accustomed to base-12. Moreover, as Ifrah demonstrates, remnants of a base-5 system of counting seems to appear in the number words for 1 to 10 of the spoken Sumerian language.

A base-60 numeral system has the disadvantage that is poses a huge load on the human memory because one would have to memorize different names for all of the numbers from 1 to 60. But the Sumerians overcame this difficulty with the trick of using 10 as an intermediary base of their numeral system. So they named the numbers between 1 and 60 essentially by using the same principle as we do, combining special names for each multiple of 10 below 60 with the names of the numbers from 1 to 9. This amounts to using a decimal system for numbers up to 60. This also influenced the way that numerals were later written using cuneiform symbols.

The Akkadian-speaking people, who dominated the later Babylonian empire in Mesopotamia, were of Semitic origin, and they were used to a decimal numeral system. They continued to use it, but in writing they first adopted the Sumerian base-60 system and only slowly transformed it for everyday use to a notation that was better adapted to oral number names with a decimal structure. This process was facilitated by the Sumerian use of base-10 as an intermediary system for the numbers up to 60. But the base-60 system continued to be used by Babylonian scholars throughout the second and first millennium BCE.

On the basis of the Sumerian numeral system, the Babylonian astronomers and mathematicians developed, probably around 1900 BCE, a very advanced method of writing numerals in cuneiform script. This written numeral system was the first place-value system in history. They used only two different cuneiform symbols, a vertical wedge meaning 1 and a chevron meaning 10. From these basic symbols they created composite symbols, which played the role of “digits” with values from 1 to 60. These digits were created by using as many chevrons and wedges as needed. For example, 56 would be written as in figure 3.1:

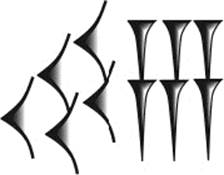
Figure 3.1: The “digit” representing the number 56 in cuneiform script.

In this manner, a symbolic notation was created for all the basic numerals from 1 to 59. In a place-value system, larger numbers are written by positioning the basic numerals next to each other in a row. This is the way we currently combine our digits. The Babylonian “digits” thus had a place value. The single wedge could mean 1 or 60, or even 60 × 60 = 3600, depending on its position in a numeral. For example, the chain of cuneiform symbols in figure 3.2 combines the “digits” for 12, 35, and 21 in a single numeral.

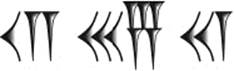
Figure 3.2: The number 45321 in cuneiform script.

The numerical value of the combined numeral is obtained by adding the place-values of each “digit.” Thus the number represented in figure 3.2 is 12 × 60² + 35 × 60 + 21 = 45321.

At first sight, this might seem like a complicated way to represent a number. But, actually, it is quite familiar to us. Whenever we measure times in hours, minutes, and seconds, we follow exactly the same technique. Assume that the number in base-60 shown in figure 3.2 represents a time measured in seconds, and its meaning becomes quite clear. The next sexagesimal unit would be 60 seconds (a minute), and 60 minutes gives an hour. Hence the number in figure 3.2 simply means 12 hours, 35 minutes, and 21 seconds. For us, this is much easier to interpret than in the decimal system as 45,321 seconds. But we are not very comfortable in using sexagesimal units. The next higher unit, 60 hours, would be a unit of two and one-half days, for which we have no name, so this is where our system for time measurement deviates from the sexagesimal system.

For a long time the Babylonians had no “zero,” that is, no symbol to indicate the absence of a unit in a number, which certainly posed some problems. If we had no symbol for zero, we could not distinguish 1 from 10 or 100. So whether a wedge „ meant 1 or 60 or 3600 had to be inferred from the context. If a unit of a given order of magnitude was missing in the middle of a numeral, they sometimes left a blank space at the corresponding position. It was probably in the third century BCE that a symbol for zero emerged, invented by Babylonian scholars. In figure 3.3, the symbol denotes the absence of the position for 60² = 3600.

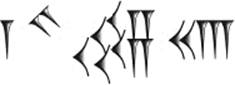
Figure 3.3: The number 1 × 60³ + 0 × 60² + 54 × 60 + 23 = 219,263.

It has to be mentioned that the Babylonian system was also used to express sexagesimal fractions in the place-value system. In our decimal system, a decimal fraction would be written, for example, as 1.11, which means 1 + + . Whenever the digit 1 appears behind the decimal point, it could mean or , and so on, depending on its position. This is completely analogous to the Babylonian base-60 system. The only problem was that the Babylonians did not invent something like a decimal point. What the writer had in mind had to be guessed, which was not always easy. The chain of symbols in figure 3.2, which we interpreted as 12×3600 + 35×60 + 21, could also mean 12×60 + 35 + , or 12 + + , and so on. It had to be decided from the context which variant was intended by the scribe. This certainly required an increased attention and logical thinking on the part of the reader, and it was also a source of errors.

The abstract Babylonian way of writing numerals had a profound influence on the scholars of antiquity. Greek astronomers, although used to a decimal system, translated the cuneiform script into their own “alphabetical” way of writing digits. However, they adopted the Babylonian system, in particular, for expressing negative powers of 60. It would have been too much work to convert thousands of astronomical tables into a decimal system. It is for that reason that we still measure units of time as well as units of angle in a sexagesimal system, dividing hours and degrees into minutes and seconds.