Numbers: Their Tales, Types, and Treasures.

Chapter 3: Numbers in History

3.3.ARITHMETIC IN EGYPT

The Egyptian way of doing calculations was based on reducing everything to addition. This is because addition of two numbers is so easy to do with this kind of numeral system. Consider for example, the computation in figure 3.6. In order to add the two numbers 2578 and 1859, you would just collect the symbols of the same kind and replace a group of ten symbols with the symbol of the next-higher order. The result 4437 can be easily read off:

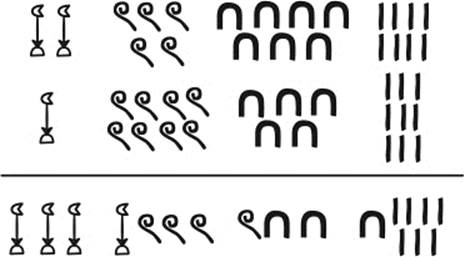
Figure 3.6: Adding two numbers.

Multiplying a number by 2 is easy because we only have to add the number to itself. Multiplying a number by 10 is even easier, because one only has to replace each symbol in the given number by the symbol of the next-higher order. Multiplying by any other number was reduced in an ingenious way to the task of addition and multiplication by 2. This is best explained by the following example:

If an Egyptian scribe wanted to multiply 12 by 58, he would create a table with two columns, starting with 1 and the multiplier 12, and double each entry in successive rows, as shown in table 3.1:

Table 3.1: Multiplying 12 by 58.

He would stop when reaching 32 in the first column, because the next doubling would lead to a number larger than 58 (the larger of the two numbers being multiplied) in the first column. The numbers in the second column are just the corresponding multiples of 12—for example, 192 = 16 × 12. Next, the scribe would mark all lines for which the sum of the numbers in the first column would give 58. This appears to be difficult at first sight but can be easily done as follows. We start from the bottom and mark the last line. Then we add the number 16 from the line above to 32, which gives 48. This is less than 58, hence we mark this line as well. We continue in this way, by adding the numbers in the first column and marking the lines, as long as the result is less than the desired multiplier. In our example, adding 8 to the previous result gives 56, which is still less than 58, therefore we mark this line. Adding 4 would give us 60, which would be too large. Therefore, we omit the line beginning with 4. Finally, adding 2 to 56 gives us the sought-after multiplier 58. Therefore, we mark the line beginning with 2. The first line is not needed. We have now marked the lines with 2, 8, 16, and 32 on the left side, and indeed 2 + 8 + 16 + 32 = 58. Now, to get the product of 12 × 58, you just have to add the numbers from the second column of the marked rows as follows:

12 × 58 = 24 + 96 + 192 + 384 = 696.

You might wonder if this method always works. Is it indeed possible to write every multiplier as a sum of the numbers in the first column of the table? Yes it is! The reason is that the numbers in the first column are just powers of 2. Hence, what is effectively done with this method is to express the multiplier in the binary system, as a sum of powers of 2:

58 = 1 × 2⁵ + 1 × 2⁴ + 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰ = 111010
(in base-2)

For example, if we want to know 12 × 45, we would have to express 45 as a sum of powers of 2, that is, as a sum of the numbers in the first column of that table. We find that 45 = 1 + 4 + 8 + 32.

We then take the corresponding numbers on the right side of the table, which are then added to give the result:

12 × 45 = 12 + 48 + 96 + 384 = 540.

We see that multiplication can be done without memorizing any large multiplication tables, except doubling numbers.

Division can be done in an analogous way, as long as the division is without a remainder. For example, in order to divide 636 by 12, one would start with the same table as before (see table 3.2).

Table 3.2: Dividing 636 by 12.

However, now we would try to write 636 as a sum of the numbers on the right side. One finds, that, indeed, 636 = 384 + 192 + 48 + 12. We then mark the corresponding lines, this time on the left side. Adding the numbers next to the check marks gives us the number of twelves that fit into 636, namely 1 + 4 + 16 + 32 = 53. Hence 636 ÷ 12 = 53.

This method only works when the division is without a remainder. The method is considerably more complicated in general cases and involves fractions. The Egyptians knew fractions, but only of the form with the numerator 1, the so-called unit fractions. The only exceptions were the very frequent expressions and , for which they had their own symbols.

In order to denote a unit fraction, they wrote a mouth symbol over the corresponding number (see figure 3.7 for examples).

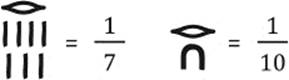
Figure 3.7: Egyptian unit fractions.

The preference for fractions of the type is probably due to their method of division. For example, when they wanted to divide 23 by 16, they would try to write 23 by adding fractions of 16. A corresponding table is table 3.3:

Table 3.3: Dividing 23 by 16.

Checked are the lines for which the sum of the numbers on the right yields 23. Adding the corresponding fractions on the left side provides the result

This represents the result as a sum of unit fractions. Again, this is a special case and the Egyptians have found more complicated methods to deal with general cases. For all fractions of the form they used tables that expressed these as a sum of unit fractions. An interested reader may wish to investigate these extensions further.