Numbers: Their Tales, Types, and Treasures.

Chapter 4: Discovering Properties of Numbers

4.3.EVEN AND ODD NUMBERS

Early humans used little stones or pebbles as an aid for counting and simple arithmetic and as a means for exploring number properties. In Latin, a pebble used for counting was called calculus (meaning “little limestone”)—the English word chalk refers back to this original meaning. Later, the Latin verb calculare meant “to reckon, to compute,” which is also the modern meaning of the English verb “to calculate.”

Probably our ancestors also had fun laying out calculi (plural of calculus) on a flat surface to produce regular shapes (such as triangles and squares), just as today's children have fun arranging their toy blocks or drawing points on a sheet of paper in regular patterns. When humans started to think about the world of numbers, they also started to explore the possible shapes and patterns that could be created with a certain number of calculi. The method of representing numbers as geometrically arranged objects or points is indeed very old and was certainly used by Pythagoras and the Pythagoreans around 500 BCE.

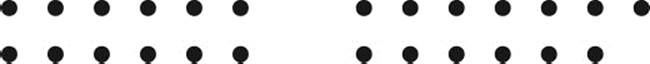
Figure 4.1: Even and odd numbers of objects.

One of the simplest observations that can be made by laying out a number of objects is about pairing. Depending on the total number of objects, we can either group all the objects in pairs, or precisely one object remains unpaired, as in figure 4.1. If it is possible to arrange a group of objects in pairs, we call the number even. Otherwise, when there is one object left over, it is called odd.

An understanding of even and odd might well have been achieved before the ability to count. Georges Ifrah, in his book The Universal History of Numbers, recounts the reports of early ethnologists about certain Australian and Oceanian aborigines who were only able to verbally express the numbers one and two.⁴ They were able to count up to four using the numerals one, two, two-one, and two-two, calling all higher numbers “a lot.” But even for larger numbers they appeared to have a clear feeling of even and odd to the extent that if two pins were removed from a set of seven, the aborigines hardly noticed it, but they saw immediately if only one pin was removed. To them, the numbers five, six, and seven were just “a lot,” but obviously they could perceive the number six as a group of pairs, which makes it quite different from five and seven—thereby distinguishing between odd and even quantities.

Using today's abstract understanding of number, we describe a number as even if the collection contains precisely twice as many objects as it contains pairs. If the number of pairs is n, then the number of objects is p = 2n. We can thus characterize an even number p as follows:

A number p is even whenever p = 2n, where n is some natural number.

We have an odd number of objects if the attempt to arrange them in pairs results in one object remaining without a partner. An odd number q thus consists of n pairs and one remaining object:

A number q is odd whenever q = 2n + 1, where n is some natural number.

A special case remains with q = 1. From today's perspective, it makes sense to call 1 also an odd number, because if we have one object, we can form zero pairs and the one and only object is always left without a partner. This just means that we can let n = 0 in the formula q = 2n + 1. Likewise, we consider zero an even number (by allowing n = 0 in the formula p = 2n).

In history, this was not always considered obvious. Aristotle, in his Metaphysics, describes the views of the Pythagoreans on even and odd numbers, whose identification of number properties with philosophical principles is certainly not easy to understand. It was explained by Aristotle as follows:

Evidently, then, these thinkers also consider that number is the principle both as matter for things and as forming both their modifications and their permanent states, and hold that the elements of number are the even and the odd, and that of these the latter is limited, and the former unlimited; and that the One proceeds from both of these (for it is both even and odd), and number from the One; and that the whole heaven, as has been said, is numbers.⁵

We talked already about the special role of the “One.” The use of the words limited and unlimited in this context needs some explanation. Of course, the Greek scholars knew that there are infinitely many odd numbers. In what sense did the odd numbers represent to them the primary philosophical principle of “limitedness”? Giovanni Reale (1931–2014), in his book A History of Ancient Philosophy, gives the following interpretation (see figure 4.2). For an odd number, division into two parts ends with the one in the middle, which is perfectly meaningful. On the other hand, dividing an even number into two equal groups leaves an empty space in the middle, which, to the Pythagoreans, meant something without number and hence incomplete or “unlimited.” This view of the unlimited nature of even numbers, as opposed to the limited nature of odd numbers, is illustrated in figure 4.2. In modern language we would just say: An even number can be divided by two without remainder, while an odd number divided by two always results with a remainder of 1.⁶

Figure 4.2: Even and odd: Division into two equal groups (demonstrating a remainder).