Numbers: Their Tales, Types, and Treasures.
Chapter 4: Discovering Properties of Numbers
4.5.TRIANGULAR NUMBERS
Another common shape is the triangle. In the days of Pythagoras, dots were arranged in a triangular shape, as shown in figure 4.9:
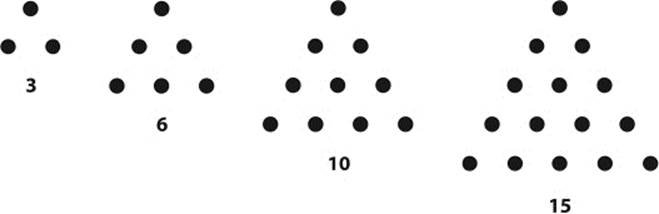
Figure 4.9: The first triangular numbers.
While the Greek philosophers would not have included the number 1, it is included today in the list of triangular numbers, as it is included in the list of square numbers. So the sequence of triangular numbers is
1, 3, 6, 10, 15, 21, 28, 36, 45,…
Let's now try to find a rule that enables us to find a triangular number, given the previous one. The solution is in figure 4.10.
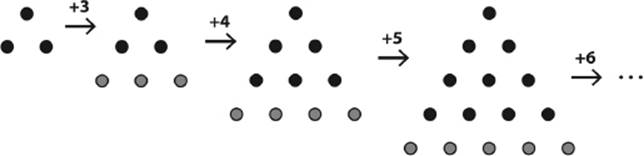
Figure 4.10: Generating triangular numbers by adding natural numbers.
We obtain the next triangular number just by adding a row at the bottom of the previous triangle. Every row has one dot more than the previous row. So the triangular numbers are simply created as sums of natural numbers:
|
1 |
= 1, |
|
|
1 + 2 |
= 3, |
|
|
1 + 2 + 3 |
= 6, |
|
|
1 + 2 + 3 + 4 |
= 10, |
|
|
1 + 2 + 3 + 4 + 5 |
= 15, |
and so on.
The following formula states that the nth triangular number, which we conveniently call Tn, is given as the sum of all natural numbers up to n (always including the number 1):
Tn = 1 + 2 +…+ n, where n is any natural number.
The triangular figure for 10 = 1 + 2 + 3 + 4 is just the familiar arrangement of bowling pins. For the Pythagoreans, this shape had a special meaning. It was called the tetraktys and was seen as a divine symbol of perfection representing the whole cosmos, including the sum of all possible dimensions. The first row, a single point, is the unity that generates all other dimensions. With the two points in the second row, they believed that one could represent a one-dimensional line. The third row, which consists of three points, can be arranged as a triangle in a two-dimensional plane, and the third row, which has four points, can be arranged to outline a three-dimensional figure, namely a tetrahedron. The sum of all these is ten, the Dekad, which was also the base of the number system that was already in use in ancient Greece. In the Attic numeral system that was used by the Athenians in the fifth century BCE, the numeral for ten was Δ, a Delta, which was the first letter of the word Deka (Δεκα), indicating ten, and one can't help noticing the similarity between Δ and the triangular outline of the tetraktys.