Numbers: Their Tales, Types, and Treasures.
Chapter 4: Discovering Properties of Numbers
4.7.POLYGONAL NUMBERS
If we take this discussion further, we enter a realm of numbers referred to as polygonal numbers, which get their name from the notion that these numbers can be placed in an arrangement that forms a regular polygon—one whose sides and angles are congruent. These polygonal numbers further enhance the appreciation of special numbers.
As we indicated earlier, three dots can be used to form an equilateral triangle, as can six dots. Therefore 3 and 6 are triangular numbers, as are 10 and 15 (see figure 4.9). We also recall that square numbers—such as 4, 9, 16, and 25—get their name from the fact that they can be arranged to form a square, as shown in figure 4.5.
Mathematicians soon started to think about possible generalizations to other regular polygons, for example, numbers that can be arranged to form regular pentagons. This is not too obvious and can be done in different ways. We learned how it was done in ancient Greece from the remaining fragments of a book on polygonal numbers written by Diophantus of Alexandria, who probably lived in the third century CE. Diophantus credits the definition of polygonal numbers to the Greek mathematician Hypsicles (who lived in the second half of the second century BCE).
The description given by Diophantus suggests that pentagonal numbers were constructed as shown in figure 4.14. These numbers begin with 5, 12, 22, and 35.
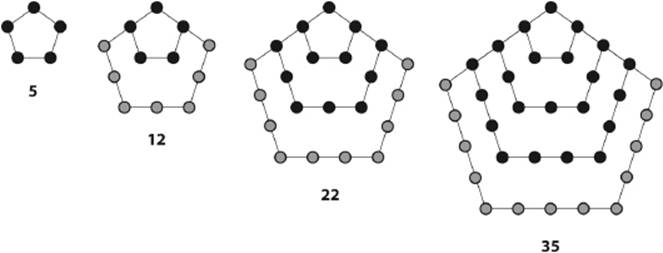
Figure 4.14: Pentagonal numbers.
The construction of these numbers follows a principle analogous to the case of triangles and squares, but it is not as elegant, because the larger figures do not have the same symmetry as the first one (since one of the corners plays a special role).
Next would be hexagonal numbers, which, similarly, represent the number of dots needed to form regular hexagons. These are the numbers 6, 15, 28, and 45 (see figure 4.15).
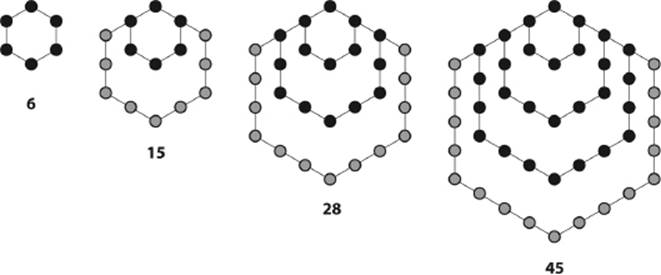
Figure 4.15: Hexagonal numbers.
Figure 4.16 lists the first polygonal numbers, again including 1 as the first element of each sequence. The numbers in between are the differences between adjacent polygonal numbers.
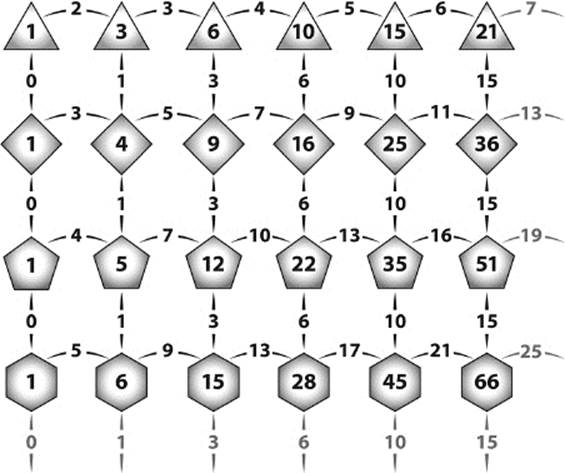
Figure 4.16: Relations between polygonal numbers.
Inspecting figure 4.16 more closely, we see that the polygonal numbers in the same column all have the same difference, and this difference is always a triangular number. For example, the fifth pentagonal number (35) has 10 dots more than the fifth square number (25) and 10 dots fewer than the fifth hexagonal number (45), and the difference 10 is just the fourth triangular number.
But this also means that any polygonal number can be obtained from triangular numbers. From the columns of figure 4.16 we can read off that the pentagonal numbers are obtained as
5 = 3 + 2 × 1 = T2 + 2T1,
12 = 6 + 2 × 3 = T3 + 2T2,
22 = 10 + 2 × 6 = T4 + 2T3, and so on.
This leads us to the general formula for the nth pentagonal number, which we denote by Pn:
Pn = Tn + 2Tn-1.
With our formula for Tn, which we obtained earlier, this can be rewritten as follows:
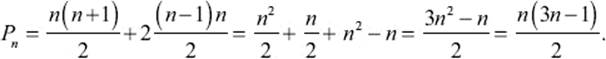
Formulas for all other polygonal numbers can be obtained in a similar way. The following formula, which Diophantus attributes to Hypsicles, gives the number of dots in a regular polygon (arranged in a way analogous to that of figure 4.14 and figure 4.15) where the polygon has k-vertices and its outer sides are made of n dots:
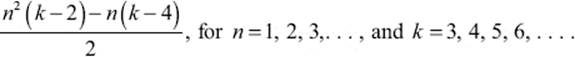
The reader may wish to check that this gives the right result for triangular numbers (k = 3), square numbers (k = 4), and pentagonal numbers (k = 5).
The construction of a polygonal number from the previous one involves the addition of a certain number of dots, which is also indicated in figure 4.16. This number, called the gnomon, is geometrically represented by the gray dots in figure 4.14 and figure 4.15 for the pentagon and the hexagon. Inspecting the lines of figure 4.16, we see that for triangular numbers the gnomon increases by steps of 1, and for square numbers it increases by steps of 2, which we have already established earlier. From the third line in figure 4.16 we see that the gnomon of pentagonal numbers increases in steps of 3, and for the hexagonal numbers in line 4 it increases in steps of 4.
We then see that every pentagonal number is a sum of integers differing by three; for example,
1 + 4 + 7 + 10 = 22, which is a pentagonal number.
So, for example, if we want to know the sum of the first n integers from the sequence of numbers that starts at one and increases in steps of three, the answer is the nth pentagonal number:
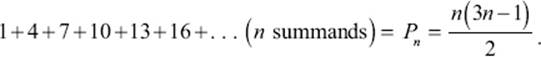
You may now ask, what sort of truth about the universe can be obtained from considering polygonal numbers? What sort of philosophical insight into first principles did the Greek scholars of antiquity get from these considerations? Are there applications for polygonal numbers? Well, the consideration of polygonal numbers has certainly spurred the growth of mathematical knowledge. But it appears that the main motivation for this study is not its possible usefulness. It is much more the fascination with the unsuspected beauty and regularity that gives meaning to numbers that had no meaning before. It is the appearance of order in an initially hardly comprehensible variety of phenomena. Here, mathematics has become an art in itself that needs no external motivation.