Numbers: Their Tales, Types, and Treasures.

Chapter 1: Numbers and Counting

1.4.THE COUNTING PRINCIPLES

The act of counting is governed by five principles. They describe the conditions and prerequisites that make counting possible. We call them the “BOCIA” principles—from the words Bijection, Ordinality, Cardinality, Invariance, and Abstraction. They were proposed by Rochel Gelman (1942–) and C. R. Gallistel (1941–) within the field of cognitive psychology, where they can be used to describe and classify typical counting errors of children. Every child who learns to count masters these principles intuitively, through practice and experience, by trial and error.

In this section, we give a brief description of each of these principles. In the following sections, we elaborate on these principles in more detail and show how they are related to some fundamental mathematical observations. An awareness of the inherent complexities of the counting procedure will also help us to better understand the psychological dimension of the number concept in chapter 2, the intricacies of the historical development described in chapter 3, and the philosophical problems with the foundations of mathematics in chapter 11.

1. Bijection principle (one-to-one principle):

When we count the objects of a collection, we associate these objects with number words. We do this in a one-to-one manner—that is, we pair each object with a unique “counting tag.” See figure 1.3.

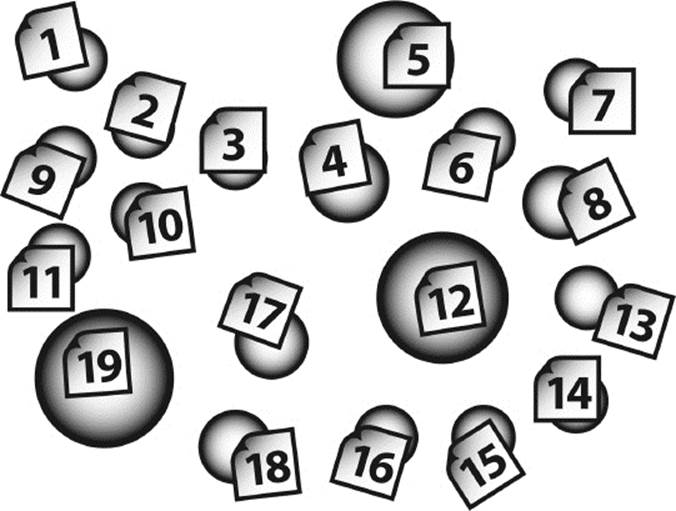
Figure 1.3: Counting is a process of pairing objects with counting tags.

In practice, counting is often done by pointing a finger at each object while reciting the well-known sequence “one, two, three,…,” and so on. When we do so, we have to be careful about the following two points:

· We have to point to each object once and only once. (In that way, no element is left without a counting tag and no element receives two.)

· We must use each of the number words only once. (In that way, two different elements of the collection cannot receive the same counting tag.)

This results in a unique one-to-one correspondence, a “pairing” between the objects and a set of counting tags, as illustrated in figure 1.3. In mathematics, a one-to-one correspondence or association is called a bijection, hence the name of this principle.

2. Ordinal principle (stable-order principle):

When we count, we do this in some order. At least in our minds, we first arrange the objects to be counted in a certain (but arbitrary) order, before we apply the counting tags to each object in turn, as shown in figure 1.4. The set of counting tags is also ordered. Typically, the name or label for the first counted object is one, then follows two, three, and so on. The order of the counting tags must not be changed when counting is repeated or when another collection is counted.

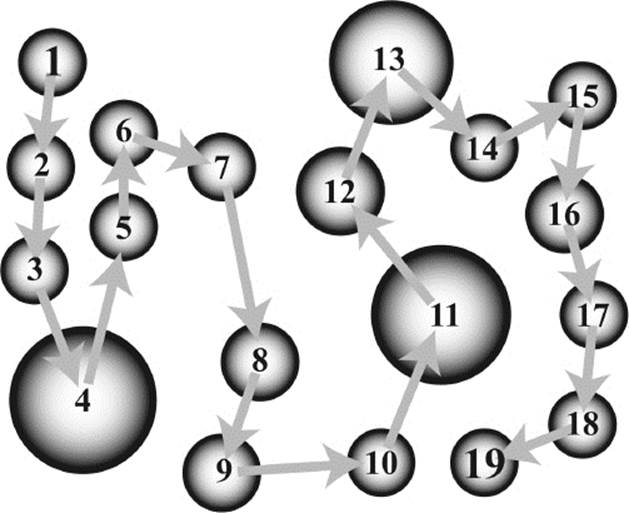
Figure 1.4: Counting by numeration (ordinal principle).

Whenever we count something, we have to use the same set of ordered counting tags. Even when the collection is apparently in disorder, we have to decide upon the order in which the objects receive their counting tags, as symbolized by the arrows in figure 1.4. In that way, the counting tags, which always follow the same order, describe or even create the order of the objects within the collection: One of the objects will be the first—where counting starts—then each object has a unique successor, until we reach the last one—where counting ends. In mathematics, numbers used to label things in a row are called ordinal numbers, hence the name of that principle.

In order to apply this principle, we have to know the sequence of number words by heart. One must be able to recite the number words in their correct order. The commonly used sequence of number words is constructed in a very systematic way, with a strict built-in ordering and without limit. Once the system is understood, one can produce as many number words as needed, and one can always name the next after any given number word in the sequence. Our number words thus provide a useful reservoir of ordered counting tags that is never exhausted, no matter how large the collection we want to count.

3. Cardinal principle:

When we start counting with one, then the last number word reached after having counted all elements of the collection has a very special meaning: It not only is the counting tag of the last counted item but also describes a property of the collection as a whole. The last counting tag is the result of counting. In everyday life we would call this the “number of objects in the collection.” The property of a collection that is described by the last number word is sometimes called its numerosity. Mathematicians call it cardinality, hence the name of that principle. The cardinality of the collection of disks in figure 1.4 is 19, or nineteen.

For young children, it is a difficult task, and a great achievement, to make the transition from the mechanical use of number words during the counting procedure (as expressed in the ordinal principle, where numbers just serve for tagging objects) to an understanding that a number word can also denote a numerosity. They have to learn that the last number word is not just the name of the last thing but a property of the whole collection. It is the answer to the question “How many?”

4. Invariance principle (order-irrelevance principle):

For the final result (that is, for the cardinality of a set), it is completely irrelevant where in the set we start counting and in which particular order we count the elements. It does not matter whether we start counting from left to right or from right to left. Figure 1.5 shows a procedure analogous to the one in figure 1.4, but it starts at another first element and proceeds in a different order, and it is a different element that receives the final counting tag, nineteen. Yet for the purpose of counting the set of pebbles, these two procedures are completely equivalent and lead to the same result. Bertrand Russell (1872–1970), in his book Introduction to Mathematical Philosophy, describes this as follows: “In counting, it is necessary to take the objects counted in a certain order, as first, second, third, etc., but order is not of the essence of number: it is an irrelevant addition, an unnecessary complication from the logical point of view.”³

Indeed, the result of counting—the cardinality of a collection—is invariant under rearrangements of the objects of the collection. The cardinality of a collection does not change if we change the order of the objects. The invariance principle thus implies that cardinality is a property of the collection and not a property of the particular counting procedure.

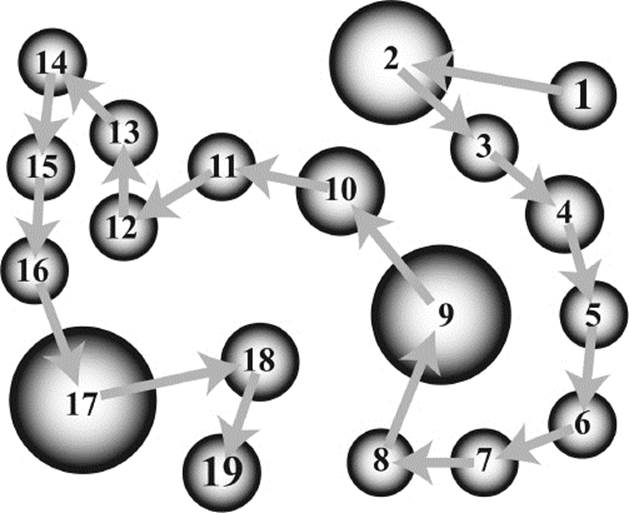
Figure 1.5: Counting in a different order (invariance principle).

5. Abstraction principle:

While the first four principles tell us how to count, the abstraction principle tells us what we can count. This principle simply states that one can count everything. Any collection of well-distinguished objects can be counted. The process of counting does not depend on the nature of the things to be counted: they may be tangible, like apples or people, or intangible, like ideas or actions. Likewise, the size of the collection to be counted is not limited (as long as it is finite). In theory, we could even count the stars in the sky or the sand of the sea, provided we have a large enough reservoir of number words so that we would not run out of counting tags.

For a child, it is again a great achievement to realize that all kinds of things can be counted, and that quite different things can be combined for counting, like toys of different shapes or immaterial things like games or actions—even numbers can be counted. And two collections that are totally different could nevertheless have the same number of elements—that is, the same cardinality. Understanding this paves the way for perceiving a number as something that has a meaning of its own, something that is independent of a concrete collection of objects.