Numbers: Their Tales, Types, and Treasures.

Chapter 5: Counting for Poets

5.11.LOTTERY GAMES AND OTHER AMUSEMENTS

We find a wealth of applications for the results in the previous section when we contemplate the problem of counting meters from a slightly different perspective.

Consider, as an example, the seven-syllable meters with two short syllables. We can create these from a sequence of only long syllables by choosing two of them and replacing them with short syllables. This would give us one of the twenty-one different seven-syllable meters with two short syllables. If we ask for the number of all different seven-syllable meters containing just two short syllables, we could also ask in how many different ways we can select two elements from a collection of seven (see figure 5.16).

Figure 5.15: Choose any two of these numbers. You can do this in B(7,2) = 21 different ways.

Quite generally, B(n,k) describes the number of possibilities to choose k objects out of n objects. Mathematicians are usually more precise when defining how to “choose.” For example, the order doesn't matter. It makes no difference if you choose first object 6 and then object 2, or if you do it the other way around. Another condition is that you can choose every object only once. In a more mathematical way of speaking,

B(n,k) describes the number of all k-element subsets of an n-element set.

The two-element subsets of the seven-element set {1,2,3,4,5,6,7} are listed in the following table; there are B(7,2) = 21 different ways to choose two numbers out of seven (see table 5.2). The particular arrangement of these subsets in table 5.2 also explains why B(7,2) is one of the triangular numbers.

Table 5.2: All two-element subsets of the seven-element set {1,2,3,4,5,6,7}.

We can now answer the following question from the beginning of this chapter:

Assume that there are n persons at a New Year's Eve party. At midnight, everybody clinks glasses with everyone else. How many clinks will you hear?

Think a moment before you read the solution in the next paragraph. Perhaps you can find the solution all by yourself?

One needs two persons to clink glasses. There will be as many clinks as you can choose two persons from the n persons at the party, that is, B(n,2) clinks. If there are seven persons at the party, you will hear twenty-one clinks. Cheers!

If alcohol is not in short supply, people might toast somebody twice while forgetting others altogether. Hence, as it is often the case, mathematics would only provide an approximate solution for the real situation.

At a New Year's Eve party, you would wish luck to your friends, maybe hoping to finally make a big win yourself—a hope that allows casinos and lottery companies around the world a carefree existence. For example, in a popular lottery game, you can choose six numbers from a set of forty-nine when you buy a ticket. Then, in a public drawing, six numbers are randomly drawn from the pool of forty-nine numbers. You would win the jackpot prize if your ticket matched all the numbers in the drawing.

The number of possible outcomes of this game is the same as the number of all possible choices of six elements out of a set of forty-nine elements—that is, B(49,6) = 13,983,816. Only one of these choices wins. Hence the probability to win in that lottery game would be

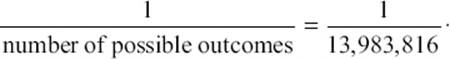
This gives a chance of about 1 in 14 million. In order to visualize that probability, imagine a chain of domino tiles on the roadside, all along the street from New York City to Niagara Falls. As the travel distance is about 400 miles, and each domino is a little less than 2 inches long, this chain would contain about 14 million tiles. Assume that one of these tiles carries a mark on the bottom side. You are allowed to stop once during your trip and pick up one of the dominoes. Would you bet on finding the marked domino with one attempt (or even one hundred attempts)? The chance to win at the 6/49 lottery is about as good (or bad). And yet, every week, millions of people pay their wager.