Numbers: Their Tales, Types, and Treasures.

Chapter 7: Placement of Numbers

7.1.MAGIC SQUARES

For some people, the expression “recreational mathematics” might be an oxymoron—a contradiction in terms, like “living dead” or “dark light.” And yet there are many people, amateurs and professionals alike, who play around with numbers and mathematical objects just for fun. And often they make very interesting discoveries. One of the mathematicians well known for his activities in the field of recreational mathematics was Edouard Lucas, who, among other things, popularized the Fibonacci numbers in the nineteenth century (see chapter 5). In the twentieth century, a well-known writer with an intense interest in recreational mathematics was American author Martin Gardner (1914–2010). During a period of twenty-five years, he published a column called “Mathematical Games” in the journal Scientific American and wrote many books on recreational mathematics.

Mathematical puzzles form an important part of recreational mathematics. They are often similar to crossword puzzles, but the entries are numbers instead of words. A famous number-related puzzle is Sudoku (Japanese for “single number”), a logic-based number-placement puzzle that originated in Japan and gained worldwide popularity in 2005. A similar, less popular puzzle, but with a closer relation to arithmetic operations than Sudoku, is known under the name Kenken or KenDoku.

One of the first puzzles in the history of mathematics was the magic square, which is as fascinating today as it was ages ago. The task is to find a square arrangement of numbers so that the sum of the numbers in each row and each column is the same as the sum of the numbers in each of the two diagonals. The first known example of a magic square is the Lo Shu square, with numbers arranged as shown in figure 7.1. It was known to Chinese mathematicians as early as 650 BCE, and it became important in feng shui, the art of placing objects to achieve harmony with the surrounding environment.

Figure 7.1: Lo Shu square and the magic turtle.

A legend from that time tells us that once there was a huge flood on the Lo River in China, and the people tried to placate the river's god. But each time they offered a sacrifice, a turtle emerged from the river and walked around the offering, until a child noticed a strange pattern of dots on the turtle's shell. After studying these markings, the people realized that the correct amount of sacrifices to make would be 15. And after they did so, the river god was satisfied and the flood receded.

The number 15 is the sum of numbers in each row, column, and diagonal of the Lo Shu magic square.

Magic squares appear throughout history; they became popular among Arabian mathematicians in Baghdad, who even designed 6 × 6 magic squares and published them in an encyclopedia in 983 CE. In the tenth century, a famous magic square, called Chautisa Yantra, appeared in India. The 4 × 4 magic square, shown in figure 7.2, is found on the Parshvanath temple in Khajuraho, India. Here the sum of each row, each column, and the diagonals is 34.

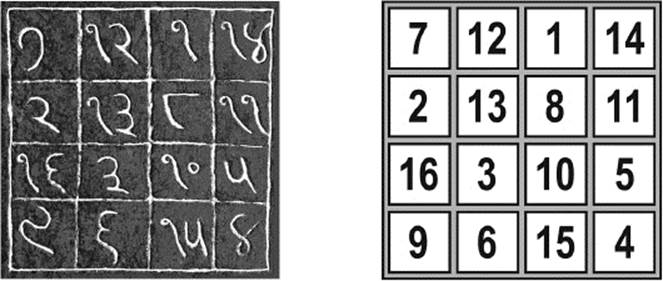
Figure 7.2: Chautisa Yantra.

There is one magic square, however, that stands out from the rest for its beauty and additional properties—not to mention its curious appearance. This particular magic square has many properties beyond those required for a square arrangement of numbers to be considered “magic.” This magic square even comes to us through art, and not through the usual mathematical channels. It is depicted in the background of the famous 1514 engraving by the renowned German artist Albrecht Dürer (1471–1528), who lived in Nürnberg, Germany. (See figure 7.3.)

Figure 7.3: Melencolia I, engraving by Albrecht Dürer (1514).

Remember, a magic square is a square matrix of numbers, where the sum of the numbers in each of its columns, rows, and diagonals is the same. As we begin to examine the magic square in Dürer's etching, we should take note that most of Dürer's works were signed by him with his initials, one over the other, and with the year in which the work was made included. Here we find it in the dark-shaded region near the lower right side of the engraving (figures 7.3 and 7.4). We notice that it was made in the year 1514.

Figure 7.4: Initials AD of Albrecht Dürer and the year 1514.
(Detail of Melencolia I.)

The observant reader may notice that the two center cells of the bottom row of the Dürer magic square depict the year as well. Let us examine this magic square more closely. (See figure 7.5.)

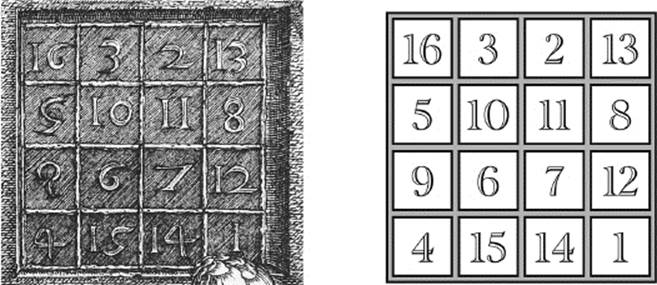
Figure 7.5: Dürer's magic square.
(Left: Detail of Melencolia I.)

First let's make sure that it is, in fact, a true magic square. When we evaluate the sum of each of the rows, columns, and diagonals, we always get the result 34. That is all that is required for this square matrix of numbers to be considered a “magic square.” However, this Dürer magic square has lots of properties that other magic squares do not have. Let us now marvel at some of these extra properties.

· The four corner numbers have a sum of 34:

16 + 13 + 1 + 4 = 34

· Each of the four corner two-by-two squares has a sum of 34:

16 + 3 + 5 + 10 = 34
2 + 13 + 11 + 8 = 34
9 + 6 + 4 + 15 = 34
7 + 12 + 14 + 1 = 34

· The center two-by-two square has a sum of 34:

10 + 11 + 6 + 7 = 34

· The sum of the numbers in the diagonal cells equals the sum of the numbers in the cells not in the diagonal:

16 + 10 + 7 + 1 + 4 + 6 + 11 + 13 =
3 + 2 + 8 + 12 + 14 + 15 + 9 + 5 = 68

· The sum of the squares of the numbers in both diagonal cells is

16² + 10² +7² +1² +4² +6² +11² +13² = 748.

This number is equal to

▫the sum of the squares of the numbers not in the diagonal cells:

3² + 2² + 8² + 12² + 14² + 15² + 9² + 5² = 748

▫the sum of the squares of the numbers in the first and third rows:

16² + 3² + 2² + 13² + 9² + 6² + 7² + 12² = 748

▫the sum of the squares of the numbers in the second and fourth rows:

5² + 10² + 11² + 8² + 4² + 15² + 14² + 1² = 748

▫the sum of the squares of the numbers in the first and third columns:

16² + 5² + 9² + 4² + 2² + 11² + 7² + 14² = 748

▫the sum of the squares of the numbers in the second and fourth columns:

3² + 10² + 6² + 15² + 13² + 8² + 12² + 1² = 748

· The sum of the cubes of the numbers in the diagonal cells equals the sum of the cubes of the numbers not in the diagonal cells:

16³ + 10³ + 7³ + 1³ + 4³ + 6³ + 11³ + 13³ =
3³ + 2³ + 8³ + 12³ + 14³ + 15³ + 9³ + 5³ = 9,248

· Notice the following beautiful symmetries:

2+8+9+15=3+5+12+14=34
2²+8²+9²+15²=3²+5²+12²+14²=374
2³+8³+9³+15³=3³+5³+12³+14³=4624

· Adding the first row to the second, and the third row to the fourth, produces a pleasing symmetry:

· Adding the first column to the second, and the third column to the fourth, produces a pleasing symmetry:

A motivated reader may wish to search for other patterns in this beautiful magic square. Remember, this is not a typical magic square, where all that is required is that all the rows, columns, and diagonals have the same sum. This Dürer magic square has many more properties. Likewise, it is worthwhile to explore the Chautisa Yantra in figure 7.2 in order to find additional properties.