Numbers: Their Tales, Types, and Treasures.

Chapter 7: Placement of Numbers

7.8.NAPIER'S RODS

Here, we introduce a calculating system that depends on the placement of numbers. The Scottish mathematician John Napier (1550–1617), who is perhaps best known for having invented logarithms and for using the decimal point in his calculations, also introduced a mechanical system for multiplication known as Napier's Rods. The method is based on a technique invented by the Arabs in the thirteenth century. When it finally arrived in Europe, it became known as multiplication “per gelosia” (“by jealousy”). It was a system for performing multiplication using only addition. Napier significantly improved the system through the use of specially constructed strips, as shown in figure 7.22. The rods can be made out of cardboard, wood, or, as John Napier did when he invented this system, bone, thus providing us with another name for this method: Napier's Bones.Before reading what follows, you may want to spend a little time examining figure 7.22 and trying to understand the logic of the construction.

The arrangement in figure 7.22 is a multiplication table. There are ten vertical rods, each of which has a specific column from the multiplication table written on it in a peculiar manner. Notice how the rod marked at the top with the digit “5” continues downward, with each of the multiples of 5 (10, 15, 20, etc.) written such that the tens digit is above the diagonal line and the ones digit is below it. The same principle can be observed in the other rods: the fifth entry on the number 7 rod is 35, which is the same as the product 5 × 7 = 35. (Observe also that we put a 0 above the slash in entries where the product is less than 10.)

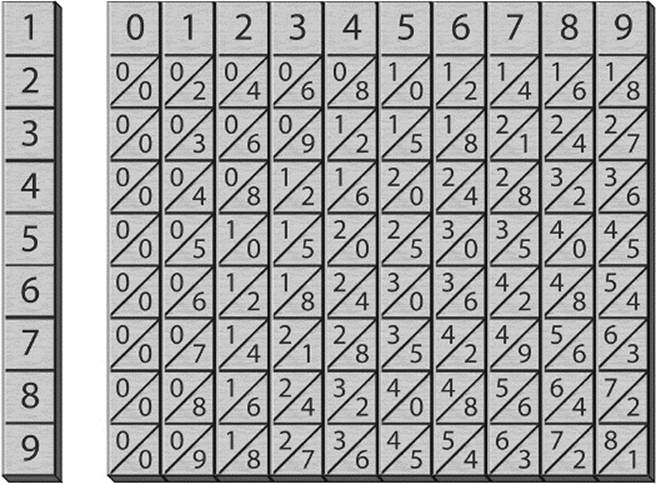
Figure 7.22: Napier's Rods.

These rods can be rearranged freely, permitting us to construct the numbers we want to multiply, and then to perform the computation using only addition. How is this possible? Let's look at an example to learn about the method Napier devised.

We will choose two numbers at random, in this case 284 and 572, and then select the rods whose top digits will allow us to construct our number. It doesn't matter which of these two numbers we choose to represent first. Thus, in this example we will construct 572, selecting the rods numbered 2, 5 and 7, and then putting them in the correct order. (See figure 7.23.)

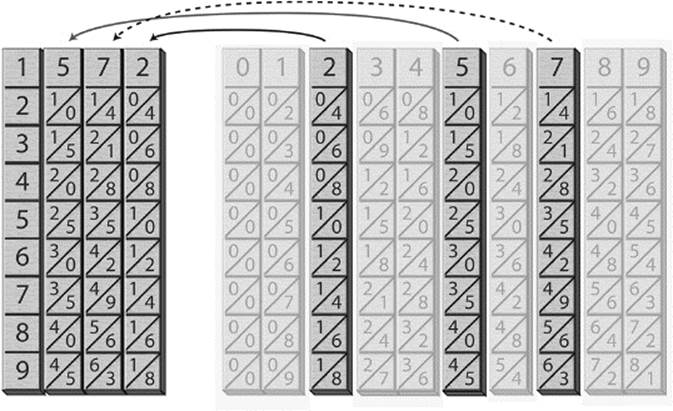
Figure 7.23: Multiplication of 572 × 284—First step.

We have written the digits 1 through 9 along the left-hand side in a single column. In Napier's original construction, these numbers were written or engraved along the side of a shallow box inside which the rods fit snugly. If you choose to re-create this example on your own, writing the numbers on a sheet of paper will work just fine, as long as you make sure to line up the tops of your own rods as you place them.

As you may have already guessed, the next step is to identify the rows that we will need to construct our second number. With physical rods it would not be possible to extract these rows, but for our illustration we will rearrange them as indicated by the arrows to form the number 284, again maintaining proper alignment. (See figure 7.24.)

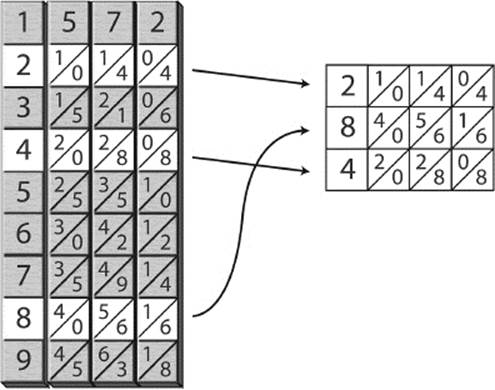
Figure 7.24: Multiplication of 572 × 284—Second step.

In order to illustrate the next step, we will de-emphasize the boundaries between the rods, while highlighting the diagonal lines. At the end of each diagonal we have created a space where our sum can be written, as indicated by the dashed arrows. It looks like our product will be a six-digit number, as there are six diagonals in our final computation. (See figure 7.25.)

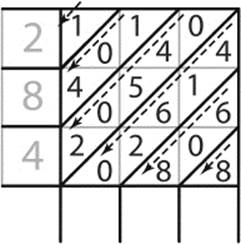
Figure 7.25: Multiplication of 572 × 284—Third step.

Starting in the lower right corner, we find the sum of each diagonal and, whenever that sum is greater than 9, write the digit to be carried in a slightly smaller font inside the box, as well as at the head of the next diagonal. Looking at the second diagonal, you can see the sum: 6 + 0 + 8 = 14, which means the tens digit of our final product will be 4, while the 1 is carried to the top of the third diagonal and added to the other numbers there, as shown in figure 7.26.

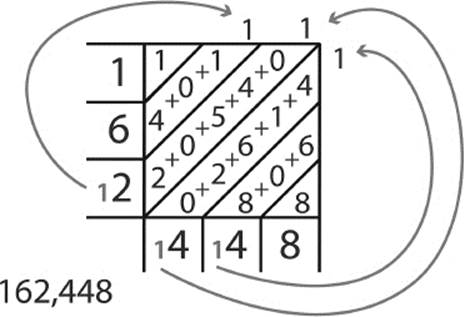
Figure 7.26: Sums of the diagonals. Addition with carrying.

Proceeding along each diagonal, we see the sums are 8, 14, 14, 12, 6, and 1. Reading these in order from the top down and from left to right, without the carried digits, we get 1 6 2 4 4 8, which indicates that our final product is 162,448. You might want to verify that this is the correct product—using our modern-day device, the electronic calculator!

Let's see how this method works. Normally, the multiplication of two numbers is performed by successive digit multiplications and positional arithmetic. When you do multiplication according to the method typically taught in elementary school, you place one number above the other with a line underneath and multiply pairs of digits. As you do so, you write the ones digit of each product below the line, carrying the tens digits when necessary, and taking the sum of the partial products at the end of the process. To illustrate how Napier's Rods work, we will break this process down step-by-step.

The first step is to multiply 572 by 4. The products of these multiplications are 4 × 2 = 8, 4 × 7 = 28, and 4 × 5 = 20. Carrying the 2 from the second multiplication and adding these together, we get a partial total of 2,288, which is the same result obtained by adding the diagonals of row four of the second figure in this section. (See figure 7.27.)

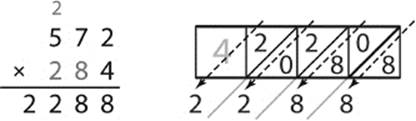
Figure 7.27: Intermediate step 1—multiplication of 572 by 4.

Repeating this process for the second digit, 8, we get 8 × 572 = 4,576, which again is the same result we get from adding the terms in the diagonals of the eighth row. According to the algorithm we know from elementary school, we insert a 0 in the ones column, leaving us with 45,760 in the new final row. (See figure 7.28.)

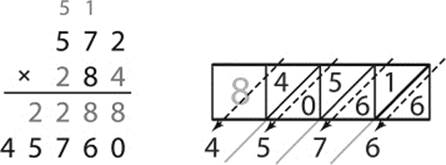
Figure 7.28: Intermediate step 2—multiplication of 572 by 8.

Next, we multiply 2 × 572 and insert two 0s, giving 114,400, the first four digits of which we recognize from the second row of Napier's Rods (figure 7.29).

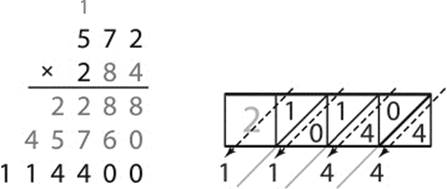
Figure 7.29: Intermediate step 3—multiplication of 572 by 2

Finally, we add these three numbers, again finding a result of 162,448, which is indeed the correct product, as shown in figure 7.30.

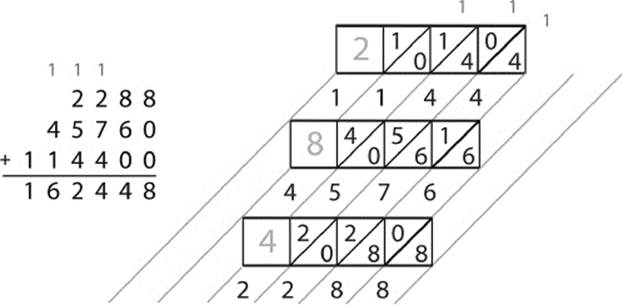
Figure 7.30: Adding the intermediate results.

To complete our illustration of this method, we will do one final alteration: instead of adding the digit products as we go, we will instead write the products as we did when constructing Napier's Rods, using a leading 0 for any number less than 10. Each product will be written with the appropriate offset, but in the same order we used when performing the previous operations.

Alongside this, we will draw the relevant portion of our Napier's Rods, this time rotated one-quarter turn as we have in figure 7.31.

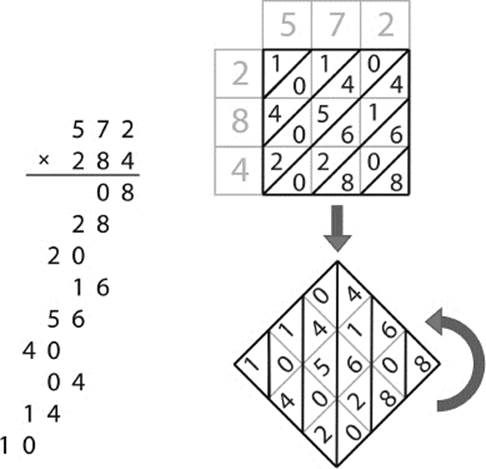
Figure 7.31: Comparison of Napier's Rods with the common method.

Do you notice anything interesting? That's right—each digit we produce using the traditional method of multiplication is also present in the Napier's Rods representation, and in the proper column! Also, if you look closely at the bold-outlined rows, you will notice that there is an exact correspondence between these rows and the respective digit products. So, for instance, the final three rows on the left are 10, 14, and 04, and these same numbers are in the top column in the figure on the right.

As we have observed, the method of Napier's Rods is mechanically identical to our elementary-school algorithm, but it can make keeping track of the positions of each digit much easier. As an added advantage, it helps us avoid multiplication errors—after all, most of us can do addition much more accurately than we can multiply!

In this chapter, we have noticed that not only do numbers demonstrate peculiarities in and of themselves but also the placement of numbers can be significant. There are surprising relationships found in magic squares, and we can arrange numbers to assist in calculations, such as with Napier's Rods. Selective number placement can also provide some curious recreations, such as the generation of palindromic numbers. Thus we can see that the position of a number can also open up some interesting vistas.