Numbers: Their Tales, Types, and Treasures.

Chapter 8: Special Numbers

8.7.THE KAPREKAR CONSTANT

An oddity that is apparently a quirk of the base-10 number system is the Kaprekar constant, which is the number 6,174. This constant arises when one takes a four-digit number with at least two different digits, forms the largest and the smallest number from these digits, and then subtracts these two newly formed numbers. Continuously repeating this process with the resulting differences will eventually result in the number 6,174. When the number 6,174 is reached and the process is continued—that is, creating the largest and the smallest number and then taking their difference (7,641 – 1,467 = 6,174)—we will always get back to 6,174. This is called the Kaprekar constant. To demonstrate this with an example, we will carry out this process with a randomly selected number. When choosing the number, avoid numbers with four identical digits, such as 3,333. For numbers with fewer than four digits, you obtain four digits by padding the number with zeros on the left, such as 0012. For our example, we will choose the number 2,303:

· The largest number formed with these digits is 3,320.

· The smallest number formed with these digits is 0,233.

· The difference is 3,087.

· The largest number formed with these digits is 8,730.

· The smallest number formed with these digits is 0,378.

· The difference is 8,352.

· The largest number formed with these digits is 8,532.

· The smallest number formed with these digits is 2,358.

· The difference is 6,174.

· The largest number formed with these digits is 7,641.

· The smallest number formed with these digits is 1,467.

· The difference is 6,174.

And so the loop is formed, since you will continue to get the number 6,174. Remember, all of this began with an arbitrarily selected four-digit number whose digits are not all the same, and will always end up with the number 6,174, which then gets you into an endless loop (i.e., continuously getting back to 6,174). It should never take more than seven subtractions to reach 6,174. If it does, then there must have been a calculating error.

Incidentally, another curious property of 6,174 is that it is divisible by the sum of its digits:

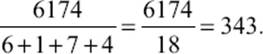
By the way, were we to apply this continuous subtraction scheme with arbitrary three-digit numbers (not all the same), we would reach the number 495, which would then result in a similar loop returning to the number 495.