Numbers: Their Tales, Types, and Treasures.
Chapter 9: Number Relationships
9.4.PYTHAGOREAN TRIPLES AND THEIR PROPERTIES
Perhaps the most popular fact that adults remember from their high-school mathematics courses is the Pythagorean theorem, which they recall as a2 + b2 = c2.
Some may even recall that the numbers a, b, and c can represent the lengths of the three sides of a right triangle. Some of the more frequently seen Pythagorean triples are (3, 4, 5), (5, 12, 13), and (7, 24, 25). We will define Pythagorean triples as follows:
· An ordered set of three natural numbers (a, b, c) that satisfy the Pythagorean relationship a2 + b2 = c2 will be called a Pythagorean triple.
Pythagorean triples were known long before Pythagoras. The Babylonian cuneiform tablet in figure 9.1 (which you might try to decipher, using chapter 3) shows a large collection of Pythagorean triples. It was made more than a thousand years before the age of Pythagoras.

Figure 9.1: Plimpton 322, a clay tablet (13 cm × 9 cm), written in cuneiform, ca. 1820–1762 BCE, presently at Columbia University. (Plimpton Cuneiform 322 courtesy of the Rare Book & Manuscript Library, Columbia University in the City of New York.)
Pythagorean triples exhibit a very unique relationship among numbers. Typically, questions arise about the nature of these Pythagorean triples, such as the following: How many such triples are there? What are some properties of Pythagorean triples? Is there a general way in which one can find these triples without just trying various combinations of three numbers to see if they satisfy the relationship? As we continue our exploration of number relationships, we will explore the responses to some of these questions as well as to others that commonly arise about the Pythagorean triples.
When the only common factor of the three numbers of the Pythagorean triple is 1, then we call that a primitive Pythagorean triple. However, there are also multiples of those triples. For example, for the Pythagorean triple (3, 4, 5), multiples of this triple also satisfy the Pythagorean theorem, such as (6, 8, 10), and (15, 20, 25), since
62 + 82 = 36 + 64 = 100 = 102, and 152 + 202 = 225 + 400 = 625 = 252.
We can justify this for the Pythagorean triple (3, 4, 5). We begin by representing a multiple of this triple as (3n, 4n, 5n), where n is a positive integer. We need to show that these three numbers satisfy the Pythagorean equation a2 + b2 = c2. Using 32 + 42 = 52, we can do this as follows:
(3n)2 + (4n)2 = 32n2 + 42n2 = (32 + 42)n2 = 52n2 = (5n)2.
This verifies that (3n, 4n, 5n) is also a Pythagorean triple. This allows us to conclude that there are an infinite number of Pythagorean triples that are multiples of (3, 4, 5).
Having established that there are infinitely many Pythagorean triples is not the whole picture, however, since the Pythagorean triples we have generated so far are all multiples of (3, 4, 5). Yet we know there are other Pythagorean triples that are not multiples of this triple, such as (5, 12, 13), (8, 15, 17), and (7, 24, 25), to name just a few. Some of the corresponding right triangles are shown in figure 9.2. One is tempted to ask, how many such primitive Pythagorean triples exist? As you might expect, there are an infinite number of such primitive Pythagorean triples. Let's investigate this further by considering various ways to generate Pythagorean triples. (For more information about the Pythagorean theorem, see A. S. Posamentier, The Pythagorean Theorem: The Story of Its Beauty and Power [Amherst, NY: Prometheus Books, 2010].)
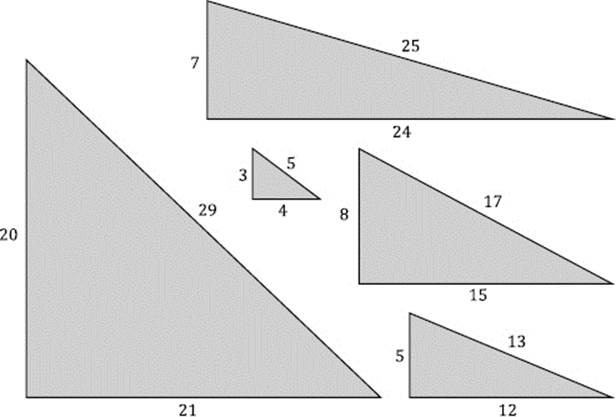
Figure 9.2: Some right triangles representing Pythagorean triples.