Numbers: Their Tales, Types, and Treasures.

Chapter 9: Number Relationships

9.6.STIFEL'S METHOD FOR GENERATING PRIMITIVE PYTHAGOREAN TRIPLES

The following approach to generate Pythagorean triples is due to German mathematician Michael Stifel (1487–1567). He created a sequence of mixed numbers of the following form:

This sequence is easy to remember: The whole number parts of the above mixed numbers are simply the natural numbers in order, the numerators of the fractions are the same number as the whole number, and the denominators of the fractions are consecutive odd numbers, beginning with 3.

Now we convert each of the mixed numbers in this sequence to a fraction. The fractions will then produce the first two members of a Pythagorean triple. For example, if we take the sixth term of this sequence, , we have the first two members of the Pythagorean triple (13, 84, c). Then, to get the third member, we simply obtain c in the following manner: c² = 13² + 84² = 169 + 7,056 = 7,225, and then take the square root of 7,225 to get 85. Thus, the complete Pythagorean triple is (13, 84, 85).

What appears as a magic trick, is, in fact, easy to explain: We can write the nth number in Stifel's sequence as

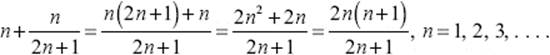
Compare this result with the general expressions for the Pythagorean triples obtained by Fibonacci's method toward the end of the last section: a_n = 2n + 1, b_n = 2n(n + 1), and c_n = b_n + 1. You can see that each of Stifel's numbers is just the quotient of the first two members of this Pythagorean triple,

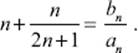
This shows that Stifel's method leads precisely to the same primitive Pythagorean triples as does Fibonacci's method.