Numbers: Their Tales, Types, and Treasures.
Chapter 9: Number Relationships
9.10.SOME OTHER PYTHAGOREAN CURIOSITIES
The following list of curiosities will further illuminate the practically boundless relationships that exist among the three members of a Pythagorean triple—once again demonstrating number relationships that further enhance one's appreciation for the beauty of mathematics.
Pythagorean Curiosity 1
We begin with any primitive Pythagorean triple—say (a, b, c). We will substitute these values of a, b, and c into the following three sets of formulas (table 9.5). Curiously, each will generate a new primitive Pythagorean triple (x, y, z):
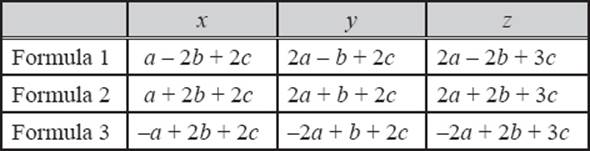
Table 9.5
To see how this works, we will apply the three formulas to the primitive Pythagorean triple (5, 12, 13), which gives the three primitive Pythagorean triples (7, 24, 25), (55, 48, 73), and (45, 28, 53) (see table 9.6).

Table 9.6
Essentially, we can use any primitive Pythagorean triple to generate three others with these three formulas. In fact, all primitive Pythagorean triples can be generated in this way from the triple (3, 4, 5), and every triple is obtained exactly once. For example, repeatedly applying formula 2 oftable 9.5 to the triple (3,4,5) would generate all the triples of table 9.4.
Pythagorean Curiosity 2
Recall the sequence of Fibonacci numbers Fn, starting with 1, 1, 2, 3, 5, 8, 13…(see chapter 6, section 1). Starting with any four consecutive Fibonacci numbers Fk–1, Fk, Fk+1, Fk+2, from the table in the appendix, section 1, one obtains the first number of a Pythagorean triple by multiplying the outer two numbers (Fk–1 × Fk+2), the second number by multiplying the middle two numbers and doubling the result (2 × Fk × Fk+1), and the third number by adding the squares of the middle two numbers (which is again a Fibonacci number F2k+1).
We can express this as a compact formula as follows:
(Fk–1×Fk+2, 2×Fk×Fk+1, F2k+1) is a Pythagorean triple for any natural number k > 1.
For example, with k = 2, we obtain the triple (3, 4, 5), because
F1×F4 = 1×3 = 3, 2×F2×F3 = 2×1×2 = 4, and F5 = 5.
And for k = 10, we obtain (consulting the table in the appendix, section 1):
F9×F12 = 34×144 = 4896, 2×F10×F11 = 2×55×89 = 9790, F21 = 10946.
Indeed, one can verify that 48962 + 97902 = 109462.
This observation is a consequence of the following formulas, which hold for all Fibonacci numbers:
(Fk+1)2 + (Fk)2 = F2k+1, and (Fk+1)2 – (Fk)2 = Fk–1 × Fk+2.
We can use Euclid's formula for generating primitive Pythagorean triples and insert for n and m two consecutive Fibonacci numbers, Fk and Fk+1. Then we get the Pythagorean triple
(m2 – n2, 2mn, m2 + n2) = ((Fk+1)2 – (Fk)2, 2×Fk×Fk+1, (Fk+1)2 + (Fk)2).
From the formulas above, we get the Pythagorean triple
(Fk–1×Fk+2, 2×Fk×Fk+1, F2k+1).
Pythagorean Curiosity 3
Inspection of the list of Pythagorean triples will convince you that the product of the first two members of a Pythagorean triple is always a multiple of 12. Therefore, we find the following result:
· The product a × b of the two smaller members of a Pythagorean triple is always a multiple of 12.
One member of a Pythagorean triple is always a multiple of 5. From this we obtain:
· The product a × b × c of all three numbers of a Pythagorean triple is always a multiple of 60.
A further still-unanswered question is whether there are two Pythagorean triples (primitive or nonprimitive) with the same product of its members.
The area of the right triangle with the legs a and b is ![]() . If a and b are members of a Pythagorean triple, the area is always a multiple of 6. A curious Pythagorean triple is (693, 1924, 2045), which just happens to have an area of 666,666. Readers involved in numerology will recognize this as a sort of double 666, which is often referred to as the “Number of the Beast” as described in the Book of Revelation (13:17–18) in the New Testament of the Christian Bible. Obviously, some Pythagorean curiosities are just that: nothing but an unusual number that raises eyebrows.
. If a and b are members of a Pythagorean triple, the area is always a multiple of 6. A curious Pythagorean triple is (693, 1924, 2045), which just happens to have an area of 666,666. Readers involved in numerology will recognize this as a sort of double 666, which is often referred to as the “Number of the Beast” as described in the Book of Revelation (13:17–18) in the New Testament of the Christian Bible. Obviously, some Pythagorean curiosities are just that: nothing but an unusual number that raises eyebrows.
Pythagorean Curiosity 4
Pierre de Fermat posed a problem in 1643 and finally found an answer himself. He sought a Pythagorean triple where the sum of the two smaller numbers is a square integer and the larger number is also a square integer. Symbolically, he sought to find a Pythagorean triple where a + b = p2and c = q2, where p and q are integers. He found one such Pythagorean triple to be (4,565,486,027,761; 1,061,652,293,520; 4,687,298,610,289), where a + b = 4,565,486,027,761 + 1,061,652, 293,520 = 5,627,138,321,281 = 2,372,1592. The third number is also a square number: c = 4,687,298,610,289 = 2,165,0172. Besides discovering this Pythagorean triple, Fermat also proved it was the smallest Pythagorean triple having this property! It is hard to imagine the next larger such Pythagorean triple.
Pythagorean Curiosity 5
We can generate a “family” of rather unusual Pythagorean triples by using the formula:
a = 2n + 1, b = 2n(n + 1), c = 2n(n + 1) + 1,
as shown in table 9.7.
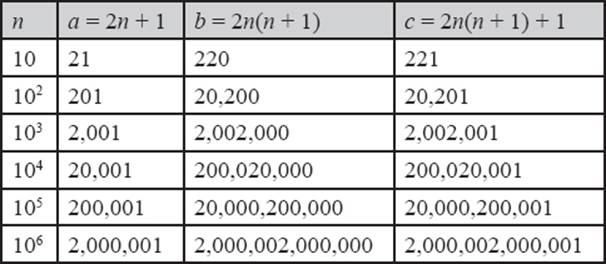
Table 9.7
You will be pleasantly surprised when you generate a similar list with powers of 20, 40, and so on in place of the powers of 10 we used in table 9.7. For n = 20, you will get 412 + 8402 = 8412, and for 202 you will get 4012 + 80,4002 = 80,4012. See what other patterns of this kind you can discover.
Pythagorean Curiosity 6
There are an infinite number of primitive Pythagorean triples where the third member is the square of a natural number. This demonstration is rather simple:
Start with two natural numbers x and y, which are relatively prime, satisfy x > y, and are of different parity (that is, one odd and the other even). Using Euclid's formula, we define a primitive Pythagorean triple by
m = x2 – y2, n = 2xy, h = x2 + y2.
(In fact, any Pythagorean triple can be obtained in this way). We can also obtain a second primitive Pythagorean triple (a, b, c) by using the Euclidean formula with m and n. In general, we could either have m > n or n > m, but in both cases,
c = m2 + n2 = (2xy)2 + (x2 – y2)2 = 4x2y2 + x4 – 2x2y2 + y4 = x4 + 2x2y2 + y4 = (x2 + y2)2.
Thus we have shown that the third member of a Pythagorean triple will be a square number whenever we use the first two members of another Pythagorean triple in the Euclidean formula to generate this second Pythagorean triple. Then this second Pythagorean triple has its third member as a square of a natural number.
For example, from the primitive Pythagorean triple (8, 15, 17) we can generate the primitive Pythagorean triple (161, 240, 289) where the third member, 289, is a square number (172).
Pythagorean Curiosity 7
In a similar fashion, we can also show that there are infinitely many primitive Pythagorean triples where one of the first two members is a square number. An example where the odd member is a square is the triple (9, 40, 41), and where the even member is a square we have (16, 63, 65). There are infinitely many of these. Pierre de Fermat proved that there are no Pythagorean triples where both first two members are square numbers. Table 9.8 shows a few examples of Pythagorean triples that have as their smallest member a square number, and some where the smallest member is a perfect cube.
|
n |
Primitive Pythagorean Triples with the Smallest Member a Square Number, n2 |
Primitive Pythagorean Triples with the Smallest Member a Cube, n3 |
|
3 |
(9; 40; 41) |
(27; 364; 365) |
|
4 |
(16; 63; 65) |
(64; 1,023; 1,025) |
|
5 |
(25; 312; 313) |
(125; 7,812; 7,813) |
|
6 |
(36; 77; 85) |
(216; 713; 745) |
|
6 |
(216; 11,663; 11,665) |
|
|
7 |
(49; 1,200; 1,201) |
(343; 58,824; 58,825) |
|
8 |
(64; 1,023; 1,025) |
(512; 65,535; 65,537) |
|
9 |
(81; 3,280; 3,281) |
(729; 265,720; 265,721) |
|
10 |
(100; 621; 629) |
(1,000; 15,609; 15,641) |
|
10 |
(1,000; 249,999; 250,001) |
|
|
11 |
(121; 7,320; 7,321) |
(1,331; 885,780; 885,781) |
Table 9.8
Pythagorean Curiosity 8
Another property of Pythagorean triples (a, b, c) is that they all have the following relationship:

For example, for the Pythagorean triple (7, 24, 25) we find ![]() , which is a square number. The converse of this statement is not true—for example, the same relationship also holds for the triple (6, 12, 18), but it is not a Pythagorean triple.
, which is a square number. The converse of this statement is not true—for example, the same relationship also holds for the triple (6, 12, 18), but it is not a Pythagorean triple.
The statement is easy to demonstrate using Euclid's formula, a = m2 – n2, b = 2mn, and c = m2 + n2:
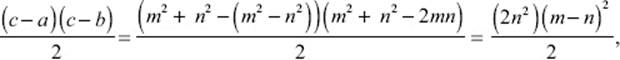
which is equal to the square number (n(m – n))2.
Pythagorean Curiosity 9
Another curiosity embedded among the many Pythagorean triples is one that relates to the Pythagorean triple (5, 12, 13). If we place the digit 1 before each member of the triple, then we get (15, 112, 113), which, curiously, is also a Pythagorean triple. This is conjectured to be the only time a single digit can be placed to the left of each member of a Pythagorean triple to generate another Pythagorean triple.
Pythagorean Curiosity 10
Some symmetric Pythagorean triples are also worth highlighting. One is where the second and third members are reverses of one another, and the first member is a palindromic number (see chapter 7, section 7). Here are two such examples: (33, 56, 65) and (3,333; 5,656; 6,565). Can you find other such “symmetric” pairs of Pythagorean triples?
There are also Pythagorean triples where the first two members are reverses of one another, such as (88,209; 90,288; 126,225). Are there more such triples?
Naturally, we can create palindromic Pythagorean triples by multiplying each of the members of the triple (3, 4, 5) by 11, 111, 111, 1111…, or by 101, 1001, 10001…, and so on. We would get Pythagorean triples that will look like (33, 44, 55), (333, 444, 555)…, or like (303, 404, 505), (3003, 4004, 5005)….
On the other hand, there are some Pythagorean triples that contain a few palindromic numbers. Some of these are: (20, 99, 101), (252, 275, 373), and (363, 484, 605). There are some where the first two members are palindromes, such as (3,993; 6,776; 7,865), (34,743; 42,824; 55,145), or (48,984; 886,688; 888,040). A more comprehensive list of Pythagorean triples with a pair of palindromic numbers is shown in the appendix, section 8.
Pythagorean Curiosity 11
For any pair of Pythagorean triples (a, b, c) and (p, q, r) the expression
(c + r)2 – (a + p)2 – (b + q)2
is a square number. Take, for example, (7, 24, 25) and (15, 8, 17). Applying his relationship we get: (25 + 17)2 – (24 + 8) 2 – (7 + 15)2 = 422 – 322 – 222 = 1,764 – 1,024 – 484 = 256 = 162.
You might want to try this for other pairs of Pythagorean triples. Again, this relationship can be proved with the help of Euclid's formula.
Pythagorean Curiosity 12
For those readers who remember complex numbers from high-school algebra, we present an unexpected connection between complex numbers and Pythagorean triples. A complex number z is composed of a real part a = Re z and an imaginary part b = Im z, and appears in the form z = a +ib. Here i = ![]() is the imaginary unit, which is characterized by the property that i2 = –1. Using this property, we can easily compute the square of any complex number:
is the imaginary unit, which is characterized by the property that i2 = –1. Using this property, we can easily compute the square of any complex number:
z2 = (a + ib)2 = (a + ib) (a + ib) = a2 + 2iab + i2b2 = (a2 – b2) + i (2ab).
Assuming a = m and b = n are natural numbers with m > n, the square of the complex number m + in is a number with real part m2 – n2 and imaginary part 2mn.
z2 = (m + in)2 = (m2 – n2) + i(2mn),
therefore Re(z2) = m2 – n2, Im(z2) = 2mn.
These are not only natural numbers, but, according to Euclid's formula, the first two members of a Pythagorean triple. The third member is m2 + n2 = (Re z)2 + (Im z)2, which is the square of the absolute value |z| of z.
Hence for two natural numbers m and n, with m > n, the complex number z = m + in defines a Pythagorean triple by (Re(z2), Im(z2), |z|2).