Numbers: Their Tales, Types, and Treasures.

Chapter 10: Numbers and Proportions

10.9.FAMOUS NUMBERS IN THE GREAT PYRAMID

Khufu, second pharaoh of the fourth dynasty, better known under his Hellenized name Cheops, ruled the Old Kingdom in ancient Egypt in about 2600 BCE. His tomb is the oldest and largest of the monumental pyramids and is built on the plateau of Giza, near Cairo. How could people who had just escaped the Stone Age have built such a gigantic monument in a perfect geometrical shape? The base of the pyramid is an almost-perfect square. The average length of its sides is s = 230.36 m, with a maximal deviation of 3.2 cm. Indeed, this precision is remarkable because the Egyptians had, at best, rather primitive tools at their disposal, which, however, were accurately manufactured and handled with extreme care. Today, it is not an easy task to measure the dimensions of the pyramid, because natural erosion and stone robberies left it severely damaged. It was, however, possible to measure the side-length of the base precisely because some of the casing stones of the base were still preserved in their original position. In particular, the location of the corner stones could be precisely determined.

It is believed that the side length of the square at the base was exactly 440 royal cubits. A royal cubit is the ancient Egyptian unit of length, divided into 7 palms or 28 fingers. Using 230.36 m for the side length of the pyramid, we find that a royal cubit must be 52.35 cm, which agrees quite well with other sources.

Much more difficult than a measurement at the base is the determination of the height of the pyramid. Today, the top of the pyramid is gone. It is still 138.75 m high, but originally it was almost 8 m higher. A rather plausible estimate for the original height is 146.5 m. From this, we can compute the slant angle of the faces of the pyramid to be 51˚49ʹ30ʺ, which corresponds well to the measured values (which are not expected to be very accurate).

Throughout the history of pyramid research, people have often speculated that the dimensions of the pyramid contain some hidden message. Pseudoscientists, pyramidologists, and numerologists have looked for curious relationships in the numbers characterizing the proportions of the pyramid. In the nineteenth century, Scottish astronomer Charles Piazzi Smyth (1819–1900) conducted several expeditions in order to measure all dimensions of the Great Pyramid. He combined the measured values in all possible ways and evaluated all possible ratios in order to find some hidden treasures in the numbers provided by the pyramid. We will consider these findings and compute a few of the typical proportions of the great pyramid.

We shall start by computing the height of the triangular face of the pyramid, the slant height d, as shown in figure 10.15. We can evaluate d with the help of the known length s of the side and the known pyramid height h. The shaded triangle in figure 10.15 is a right triangle, hence we apply Pythagorean theorem as follows:

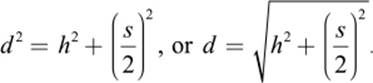
Inserting h = 146.5 m and s = 230.36 m, we obtain d = 186.356 m. Let us now compute the ratio between d and —that is, the proportion of the two bold lines in figure 10.15.

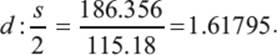
This number is surprisingly close to the golden ratio ϕ ≈ 1.61803. Could it be that the architects of the pyramid indeed chose to encode the golden ratio in the proportions of this pyramid?

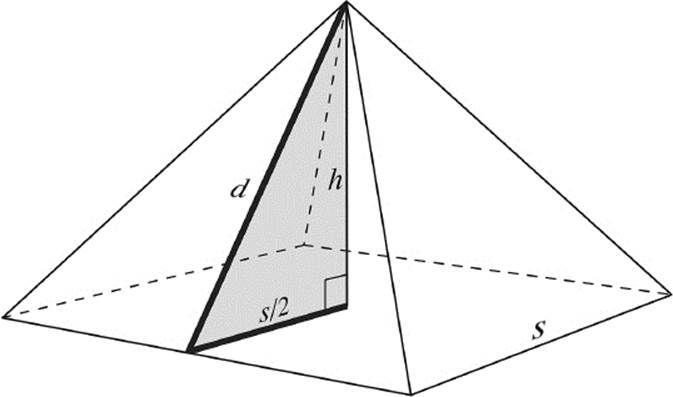
Figure 10.15: Slant height:half-side length = the golden ratio.

We can determine the height h of the pyramid that would be required for the above proportion to be exactly the golden ratio. The computation gives h = 146.511 m. This value deviates only 11 mm from the original estimate (146.5 m). It is clear that such minimal differences could not make any difference in a structure of that magnitude. Moreover, the inaccuracy of determining the height is much larger given the present-day condition of the pyramid. Therefore, the measured dimensions of the pyramid would support the following hypothesis:

Hypothesis 1: The Great Pyramid of Cheops is designed in such a way that the slant height and the half-side of its base are in the proportion of the golden ratio:

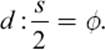
Now the big question is whether it was planned that way or whether everything is mere coincidence. It is safe to assume that the Egyptians of that time did not know the golden ratio and that to them this proportion could not have the mathematical importance that was assigned to it more than two thousand years later by Greek mathematicians. So why should they encode the golden ratio in the dimensions of the pyramid?

An often-quoted explanation has its origin in the writings of American pyramidologist John Taylor (1781–1864), who referred to the Greek historian Herodotus (ca. 484–425 BCE). He said that the Egyptians did not intend to encode the golden ratio in the pyramid, instead they applied the following idea:

Hypothesis 2: The Great Pyramid of Cheops is designed in such a way that every face of the pyramid is of the same area as the square of the height. (See figure 10.16.)

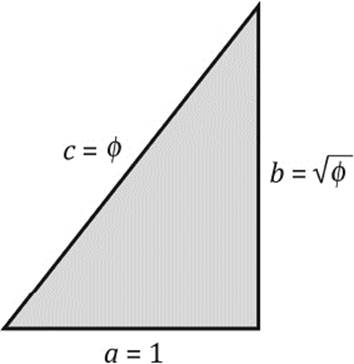
Figure 10.16: The two shaded areas are approximately equal in size.

From this hypothesis, it is a matter of elementary algebra to derive the above-mentioned proportion involving the golden ratio. The two hypotheses are consequently mathematically equivalent. But is Taylor's interpretation correct? Actually, the corresponding quote of Herodotus, the only one considering the dimensions of the pyramid, reads as follows: “The pyramid itself was twenty years in the making. Its base is square, each side eight plethra long, and its height is the same; the whole is of stone polished and most exactly fitted; there is no block of less than thirty feet.”²Here one plethron is 100 Greek feet; its exact measure is unknown. Canadian mathematician Roger Herz-Fischler, in his book The Shape of the Great Pyramid, points out that this source is not sufficient to prove Taylor's claim. The height seems to be just a rough estimate and not accurate. Taylor seems to have undertaken a radical reinterpretation of this text when he claimed that the words “and its height is the same” should not be understood as an equality in lengths, but as a quadratic equality, according to which the area of the face is the same as the area of the square with side h. Today, Taylor's interpretation appears rather dubious. Let us look for other possible explanations.