Numbers: Their Tales, Types, and Treasures.

Chapter 10: Numbers and Proportions

10.11.THE HISTORICAL EXPLANATION

The Rhind papyrus mentioned earlier contains some mathematical problems dealing with the slope of pyramids. In this connection we learned about the seked. The seked measures the slope of the face of a pyramid. The seked is the horizontal distance (in fingers) needed for a rise of one royal cubit (1 royal cubit = 28 fingers). Therefore, a steeper pyramid would have a smaller seked. The Great Pyramid of Cheops seems to have been planned with a seked of 22 fingers, which we have shown in figure 10.19.

Assuming a base length of 440 royal cubits and a seked of 22, we can again determine the height of the pyramid (actually one of the problems in Rhind papyrus). We would obtain precisely 280 cubits = 146.59 m, which is 9 cm more than the original estimate and in between the heights obtained from Hypotheses 1 and 3, respectively. Again, this result is completely in accordance with the empirically measured height of the pyramid.

Many pyramids in Egypt were built with a certain seked, and the sekeds 22 and 21 were used more than once. In order to achieve a good impression, they tried to build the pyramid as steep as possible, which led to technical problems concerning the stability of the structure. It can be assumed that a seked of 22 was the technical optimum at the time of Cheops. When this seked is chosen, the triangle in figure 10.15 becomes virtually indistinguishable from the Kepler triangle. Figure 10.20 shows three triangles: the left-most exhibits the golden ratio (Hypothesis 1 and 2), the one in the middle assumes that the horizontal side is measured by n revolutions of a surveyor's wheel, and the vertical side is given by 4n diameters of the same wheel. Finally, the right-most triangle realizes a seked of 22 (vertical gain of 28 fingers over a horizontal distance of 22 fingers). Even if they were to have been drawn on a larger sheet of paper, the three triangles would be identical to within the thickness of the line of a pencil.

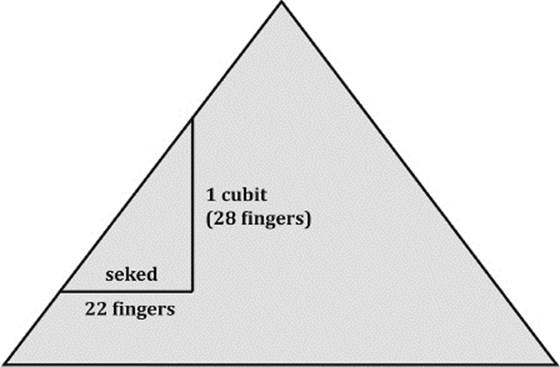
Figure 10.19: A seked of 22—the slope of the pyramid.

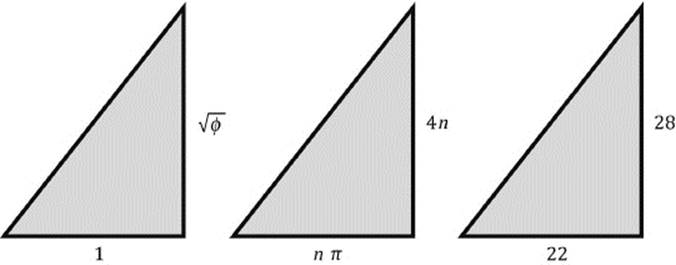
Figure 10.20: Three triangles with very similar proportions.

The explanation is simple. Just remember that a good approximation of the number π is given by the fraction . Hence the fractions

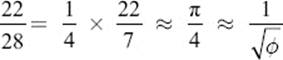
are all approximately the same. A seked of 22 automatically, and coincidentally, creates the proportion of the golden ratio together with the proportion of π in the dimensions of the pyramid. Actually, there is nothing mysterious about it, and in part it is just numerical coincidence. By the way, a seked of 21 would, instead of the triangle in figure 10.20, lead to a triangle with sides 21, 28, and 35, which is a Pythagorean triple (with proportions 3:4:5). This would lead to a pyramid with simple integer proportions, which certainly would have been preferred by the Pythagoreans.

We learn from this that not every occurrence of the golden ratio or of π, be it in architecture or in art or in nature, has a “hidden” meaning or was implemented intentionally. Very often, apparently meaningful number relations might pop up unexpectedly, seemingly hinting at a deeper reason. This gives rise to a long tradition of mystic speculations about the occurrence of certain numbers. One has to be careful about making unjustifiable generalizations. Very often, the scientific explanation, which, admittedly, is less romantic than number mysticism, reveals that there is nothing behind these speculations.