Mathematics and the Real World: The Remarkable Role of Evolution in the Making of Mathematics (2014)

CHAPTER II. MATHEMATICS AND THE GREEKS’ VIEW OF THE WORLD

14. MODELS OF THE HEAVENLY BODIES (CONT.)

Aristarchus of Samos (310–230 BCE) made a radical proposition about the motion of the heavenly bodies. He claimed that it was not the Earth but the Sun that was at the center of the universe and that the Earth and the other planets orbited the Sun. We know of the activity of Aristarchus from one essay that has survived in its entirety, in which he calculated the sizes of various astronomical bodies and distances, including the size of the Earth and the Sun, and the distance of the Earth from the Sun and the Moon. Archimedes, with whom Aristarchus was in contact, refers in his writings to the doctrine of Aristarchus. Aristarchus developed methods for calculating and measuring that resulted in assessments that were very advanced for their time but are very different from the facts as we know them today. For example, he assessed that the ratio of the distance of the Moon from the Earth to the distance of the Sun from the Earth was 1 to 19, whereas the correct ratio is 1 to 380. These and other measurements resulted in his proposing a heliocentric model (i.e., with the Sun at the center). The reason he gave was aestheticism. It was unreasonable to think that such a large body as the Sun would revolve around such a relatively small Earth. Aristarchus, who was affected by the views of the Pythagoreans, thought that the Sun was the fire at the center of the universe. He also realized that Eudoxus's model of spheres and its later developments can be more easily explained if it is assumed that the planets orbit the Sun and that the Earth also revolves on a circular path around it.

Although Aristarchus's model was widely known by the Greek astronomers, it was not generally accepted by them. There were several reasons for its rejection, some philosophical, and some scientific. The philosophical argument was the almost religious Aristotelian claim regarding the purity of the heavens as opposed to the impurity of Earth. One report states that Aristarchus himself was accused of heresy regarding those religious principles, but such accusations were not characteristic of the Greek environment that permitted pluralism of expression. The scientific objections to Aristarchus's model, however, were serious. One was that if the Earth moved around the Sun, then from different locations on its orbit the angles between the stars would be different, and that was not the case. This reason was quoted by Aristotle himself as an argument against the possibility that the Earth revolved around the Sun. It was not until many years later that the different angles between how we see the stars were revealed, differences that were too small for the Greeks to measure. Another argument against the centrality of the Sun was that if the Earth orbited the Sun, its speed would have to be so great that anything on the surface of the Earth would be propelled off it into space. We will address this claim when we discuss Ptolemy.

Further crucial progress in the calculation of cosmological data was made by Erastothenes (276–195 BCE). He was born in Cyrene, in what is today Libya, and carried out most of his scientific work in Alexandria, Egypt. He held the distinguished role of chief librarian of the widely known Great Library of Alexandria. Today's students know the name Erastothenes because of the “Sieve of Erastothenes,” an (inefficient) way of finding all the prime numbers. He took it upon himself to calculate the dimensions of the Earth. He noticed that at noon, in the city of Syene (known today as Aswan), an upright pole does not cast a shadow, whereas at the same time in Alexandria, it does. By measuring the angle of the shadow in Alexandria and the distance between the two cities, which lie on the same longitude, he managed to estimate the dimensions of the Earth. The methods used by Aristarchus, Erastothenes, and their colleagues to perform their calculations are themselves very interesting, but beyond that, they provide evidence of the progress of practical mathematics in Greece, mathematics that served the Greek engineers and builders, who made remarkable achievements. Greek mathematics, fed by Egyptian and Babylonian ideas and achievements, constituted significant further development. Archimedes of Syracuse (287–212 BCE) was perhaps the best-known mathematician of that period for his mathematics-based engineering developments. We will allude to his contribution later.

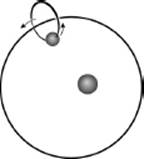
Two far-reaching proposals regarding the model of the motion of celestial bodies were made by Apollonius of Perga (262–190 BCE). One was that the center of the circle on which a planet moved was not necessarily the center of the Earth. The other was that a planet can revolve along a perfect circle around a point that is itself revolving along a perfect circle around the Earth. He arrived at these views through his research into curves in a plane, particularly those created by orbiting in a small circle, known as an epicycle, the center of which moves along a larger circle, which the Greeks called a deferent. The curve thus created orbits around the deferent in a way very similar to the way the Moon revolves around the Sun. This motion is made up of two paths that sometimes move in opposite directions. Hence the motion is not constant but is sometimes forward and sometimes backward. This irregularity, combining progression and regression, is in some way similar to the irregularity of the paths of the planets, and Apollonius therefore proposed that the epicycles around the deferent were the paths of the planets. (See the diagram below, showing the Earth not at the center of the circle and the movement of the planet along the epicycle.) These two amendments to the previously held views enabled Apollonius, of course, after detailed calculations, to present a mathematical system of planetary motion that fitted well with the facts known at that time.

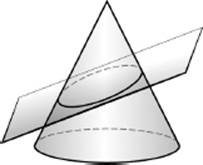
It is interesting that Apollonius, who is known for his contribution to geometry in general and who also carried out rigorous research into the properties of lines in a plane and the structure of three-dimensional bodies, was very familiar with ellipses. One of his better-known studies dealt with the structure of cones and the shape of their two-dimensional cross-sections. His research showed, for example, that the shape formed by a two-dimensional plane that intersects a cone could be a parabola, a hyperbola, or an ellipse (see the diagram below). Yet, although he was familiar with the shape of an ellipse, it did not occur to him to suggest that the paths followed by the planets were in fact ellipses. It took another fifteen hundred years to reach this conclusion.

Hipparchus (190–120 BCE) took the mathematics of the model of the motion of celestial bodies to another level. Most of what we know of Hipparchus comes from the writings of Ptolemy, who called him the greatest Greek astronomer. Hipparchus did most of his scientific work on the island of Rhodes. Thirty-five years of astronomical observations that Hipparchus carried out on Rhodes combined with astronomical data from the Babylonians resulted in his constructing an astronomical model with previously unknown precision. For example, following his studies, the Greeks could forecast an eclipse of the Moon with an accuracy of within one hour. Hipparchus also discovered and measured the precession of the equinox (which we now know is caused by the movement of the plane of the Earth's orbit with regard to the position of the stars) and calculated the length of the cycle of this movement (about 2,600 years). His measurements greatly improved the data on the sizes of the heavenly bodies, the Sun, and the Moon, as well as their distance from the Earth, and data on the seasons, the times of the equinox, and so on. Hipparchus's major mathematical contribution was in the development of trigonometry. He defined trigonometric values, such as the sine and tangent of an angle, and found basic relations between them that helped him in his calculations. Following these definitions, he himself and his contemporaries constructed tables of what is today called the sine function (see the diagram), that is, the graph of the sine of every angle (the ratio of the line opposite the angle in a right triangle to the length of the hypotenuse), as well as other trigonometric functions, such as cosine and tangent. These functions fulfilled a major role in describing nature from the time of the Greeks to today.

Hipparchus, and after him Ptolemy, adopted the geometric principles of Apollonius. Ptolemy was active in Alexandria from the year 90 CE to 169 CE, but these are approximations, as no biographies with details of his life have survived. His writings, however, have been preserved almost in their entirety, as they were copied and kept by the Arabs, and they provide much information on the model of the celestial bodies and Ptolemy's scientific approach. His main contribution was technical rather than conceptual. His basic starting point was the assumption that the heavenly bodies orbited the Earth, that their paths were epicycles whose centers were on a deferent that revolved around a point in space that was not necessarily the center of the Earth, and that the planes on which those deferents revolved were probably angled toward each other. With intensive and detailed computations, Ptolemy constructed a model, complete for his time, of the motion of the heavenly bodies. The model included seventy-two epicycles and larger cycles and represented a marked improvement on earlier models as it provided a superior fit of the observations to the model. The model gave far more accurate predictions than did the previous ones, and it remained the main model of the motion of celestial bodies for fifteen hundred years, longer than any other physical model in the history of science.

Ptolemy was aware of other ideas and approaches put forward by the Greek scientists over time and actually referred to them in his writings. He rejected Aristarchus's idea that the Earth revolved around the Sun with a quite rational claim based on calculations. Ptolemy's calculations showed that according to the heliocentric method with the Earth orbiting the Sun, the speed of the motion is incomprehensible and human thought cannot even imagine such a high speed. In particular he claimed that if the Earth revolved around the Sun, all animals and humans would fall off. He rejected with a similar argument the view still held at the time by Heraclides, namely, that the Earth revolved on its own axis. He added another argument to this, stating that if the Earth revolved on its own axis, a stone thrown upward would not fall straight down. He answered Heraclides's claim that huge cosmological bodies could not revolve around the relatively small Earth with the retort that the size of the bodies was not the determining factor, but their weight, and the Earth was very heavy, while the weight of the sky, the stars, and the ether in which they are situated is negligible. These are completely rational claims based on what our senses show us. Ptolemy acknowledged that Aristarchus's model, with the Earth revolving around the Sun, was simpler. He knew that there was contradiction between the simplicity of the mathematical theory on the one hand and what our senses perceive and the precision of the results on the other. In this situation, Plato would have preferred the simple mathematical theory. But Ptolemy's mathematical theory was so exact that it superseded the simplicity of other notions. This contrast between what our senses tell us and a simple but abstract model has accompanied science throughout the generations.

It should be stated that Ptolemy repeatedly said in his books that his model is just a mathematical description of nature. Specifically, he did not claim that his circles were a law of nature but that it was mathematics that best described nature. Moreover, he took the trouble to show that in some cases simpler models could yield more accurate results, but he was searching for a mathematical model that would incorporate all the phenomena. It was the Christian church that adopted Ptolemy's model as scientific truth and declared that God used mathematics to create the world.