Mathematics and the Real World: The Remarkable Role of Evolution in the Making of Mathematics (2014)
CHAPTER VI. THE MATHEMATICS OF HUMAN BEHAVIOR
47. THE MATHEMATICS OF CONFRONTATION
In this section we will discuss the mathematical analysis of methods of decision making by humans as individuals. What is special in a social framework is that the decisions of any particular person may clash with the activities of others, and the person making the decisions must take into consideration what his colleagues or opponents will do. At this point we can distinguish between two different scenarios. In one, the impact of the actions of the individual decision maker on say the market situation will be negligible. In the other, the actions of each one of the individual decision makers could influence the final outcome.
In the first case the decision maker assesses the circumstances he faces, and in light of those circumstances he assesses the results of the different decisions he can make and chooses what seems to him the best. The function of mathematics in this process is to construct a mathematical model that can be analyzed quantitatively, and to propose methods of reaching the optimal decision. The mathematical subject is called optimization. We will not expand on it here, because the mathematical methods it uses are not essentially different from those we have encountered previously. We will nonetheless mention the outstanding example of such a mathematical development that had a significant impact on decisions in the capital market. We are referring to the Black-Scholes model and the Black-Scholes formula, which analyzes the risks and chances incurred in investing in the capital market.
The economists Fisher Black and Myron Scholes published a paper in 1973 in which they put forward a mathematical framework that enabled them to analyze the risks involved in investing in options in the capital market. Following their paper, Robert Merton published a paper in which he extended the system and developed the mathematics to the level that it became a tool in the hands of investors in the stock market. The mathematical tool employed in the model is differential equations, which we came across in our discussions of models of natural phenomena, with the difference that the variables are not location, energy, and speed, but prices and rates of interest, and so on. The model was put to routine use by investors in the stock market, and in 1997 Merton and Scholes were awarded the Nobel Prize in Economics. Black died in 1995.
In the second of the two scenarios outlined above, the decision maker takes into consideration the reactions of other individual decision makers to his own decisions. They too act in light of their assessments of the actions of others. In this situation the use of the word optimal may sometimes mislead. For example, take the situation in which several people make their individual decisions, and the outcome is determined by their decisions combined. What is optimization in this case? Optimal for one participant may be terrible for another. If one of the group members knows or assesses the decisions of the others, he will be faced with the optimization problem described above. But then each of the others can estimate the choice of that same individual and can change his own choice accordingly. In which case, the first can alter his decision in light of the new situation, and so on. It is then not clear what the optimal decision is. The mathematical field that analyzes such situations is game theory. The rather simplistic name is likely to be misleading because this branch of mathematics is dealing with a very serious subject, the analysis of confrontation. On the other hand, the name game theory has become so accepted by the public that it is commonly assumed that the term game in this context means confrontation.
The situation that we have described is relevant also to conflicts between decision makers in daily life as well as to social games such as chess. A mathematical analysis of the theoretical possibilities in a game of chess was carried out in 1913 by the German mathematician Ernst Zermelo (1871–1953), famous for his contribution to the foundations of mathematics, whose paper titled “On an Application of Set Theory to the Theory of the Game of Chess” introduced new concepts to that area of research and provided the source of the name game theory. Other well-known mathematicians continued to develop that field, including the French mathematician Émile Borel (1871–1956), who in 1921 introduced the mixed-strategy concept, and John von Neumann (1903–1957) who in 1928 proved the minimax theory. We will meet these two concepts again later in this section. Zermelo's paper dealing with social games led to the development of the subject, which analyzes conflicts between individual decision makers, be they private individuals, company directors, or military and political leaders. The insights reached by game theory have been used since then to analyze situations of people and companies and to understand conflicts of interest between animals. With animals we cannot identify conscious decision making, but the process itself takes place as if someone were making deliberate decisions. In particular, viewing the evolutionary struggle itself as a conflict between species helps in the analysis of the evolutionary process.
Just as in other areas of specialization that mathematics uses to describe and explain phenomena, before using them we must specify precisely what framework of mathematics we are working in. One of the models in game theory is called games in strategic form (we shall allude to another model, namely cooperative games, later in the section). This is a game between several players, each one of whom must choose one of a given number of possibilities, called strategies. The choice is made simultaneously, and when each participant makes his decision, he does not know what the other players are choosing. The game ends when the decisions of all players have been received. Next, each player receives a “payoff” that depends on the combination of all the decisions taken. All the players know the payoff and its dependence on the strategies in advance. The payoff can be monetary, but it can also be in another form, assuming that the player has a full rating of preferences for the rewards he is entitled to receive. Clearly the strategic-form model does not cover all conflict situations between players. We will limit the mathematical analysis by imposing the condition that the number of strategies facing each player is finite (for discussion purposes only; the professional literature also analyzes situations with infinite possibilities). Our purpose at this point is to arrive at an understanding of what mathematics can offer at the conceptual level, and that can be achieved with a simple model. If we wish to use the results to analyze day-to-day situations we will need to check the extent to which the circumstances match the mathematical model.
Even at this level of presenting the definition of a game, we can propose “obvious” properties of the players’ possible decisions. For instance, assume that a player recognizes the following property of one of the strategies facing him, say strategy A: for every possible move by the other players, strategy A yields him the highest payoff. It is then proper for us to refer to the decision to adopt strategy A as the optimal decision. In game theory, such a strategy is called a dominant strategy. It stands to reason that a player who identifies a dominant strategy among the options confronting him will adopt that strategy. If each of the players has a dominant strategy, we have “solved” the game. However, players do not always have a dominant strategy. In those cases the best response to one's opponents’ moves is achieved via different strategies.
Another possibility that a player can choose is to look for a maximum-minimum strategy. In other words, the player can calculate the lowest payoff that every strategy might yield him and choose the best of those low payoffs. This concept describes behavior that settles for minimizing possible losses or that reflects concern over the worst-case scenario. In many situations the use of these strategies does not yield reasonable outcomes.
A crucial step in the analysis of possibilities in a game in strategic form was made by John Nash of Princeton University, New Jersey. Nash is known by the general public mainly because of the book and subsequent film, A Beautiful Mind. The book, written by Sylvia Nasar, recounts Nash's life history, from his graduate studies at Princeton University in 1948, his illness, his disappearance from the world of research, and his being awarded the Nobel Prize in Economics in 1994. Nash, who also made significant contributions in many other areas of mathematics, proposed the following definition.
Assume that every player chooses one of the strategies open to him. This collection of strategies is in equilibrium if no player can by himself earn a higher payoff by changing his strategy while the other players keep to their original ones.
The rationale underlying his definition was that if the players agreed on a choice of strategies that are in equilibrium, or if they discovered somehow that the other players would choose strategies in equilibrium, there is no incentive for any of them to switch from that strategy unilaterally.
Nash did not put forward his definition in a vacuum. Exactly the same concept had been proposed more than a hundred years earlier by the French mathematician and economist Antoine Augustin Cournot (1801–1877), who made valuable contributions to economic theory in several areas. Cournot defined the concept of equilibrium between two firms that constitute a duopoly, that is, the two firms control the market. As Cournot formulated the concept in a relatively complex model, his definition lacks the simplicity and clarity of Nash's definition, but nevertheless many show their respect for him by referring to the concept as Cournot-Nash equilibrium. Others, after Cournot, also used the same concept in various forms, but it was Nash's precise formulation that led to the recognition and widespread use of the concept. Nash went further and proved the existence of equilibrium in a framework we will describe a little later, but first we will give three examples of the concept of equilibrium that are standard in any textbook on game theory.
The first example is known as the prisoner's dilemma. Despite its eye-catching name, the game reflects situations we encounter frequently in trade, economics, our social lives, and so on. The dilemma is between cooperation that would to some extent benefit both players, on the one hand, and noncooperation that would be advantageous to one player at the expense of the other. That is indeed a common situation, but in our case each participant must make the decision without any communication with the other one. The mathematical version of the tale is of two suspects who committed a crime, but the police have insufficient evidence for a conviction without one of the suspects incriminating the other. The police therefore make an offer that if one of the suspects will testify against the other and the other continues to claim he is not guilty, the cooperative suspect will go free and the other one will be sentenced to four years in prison, the punishment prescribed by law. If neither agrees to testify against the other, it will be impossible to prove the more serious charge against them, but they can both be convicted of a lesser offense that carries a one-year prison sentence. If they both accept the offer and each agrees to testify against the other, they will both be convicted but their testimony will earn them a reduced sentence of three years. Each suspect is faced with two possibilities, or in the terminology of game theory, two strategies. One option is to testify, and the other is to refuse the offer, that is, to deny the charges. Each must make the decision without knowing what the other will do. It is customary to summarize the possibilities in the following table.

The rows in the table represent the possibilities, that is, the strategies, facing the first suspect, and the columns represent those of the second suspect. The top row shows the position when the first suspect testifies against the second, and the second row is the situation when he refuses to do so. The left column shows the position when the second suspect refuses to testify and continues to plead not guilty, the right shows when he agrees to testify against the first. The two numbers in the cells of the table show the number of years each suspect will be sentenced to as a result of their decisions; the number on the left refers to the first suspect, and that on the right refers to the second.
The reader will readily see that the table reflects what was described above verbally. Each suspect wants to minimize the number of years he will have to spend in prison. When the concepts described above are applied, it is easy to see that testifying against the other suspect is the dominant strategy for each of them. In other words, for each suspect, testifying against the other is worthwhile, regardless of what the other decides to do. Specifically, the pair of strategies in which each suspect agrees to testify is in equilibrium. According to our description of dominant strategies above, we have solved the game. Each suspect will agree to testify against the other, and the outcome will be that each will serve a three-year sentence, whereas if neither had agreed to testify they would each have served only one year.
Have we then solved the game correctly? We will return to this question further on, and here we will note that we have solved the mathematical game, but the mathematical game ignores many aspects of conflicts that we come across in our daily lives.
The second game is known as the battle of the sexes. Presented in table form, it looks as follows:
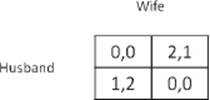
The situation is that a husband and wife have agreed to go out together that evening. He would prefer a football game as their joint destination, and she would prefer them to go to the opera (the rows represent the husband and the columns the wife). Both would prefer to spend the evening together and not go to different events. As in the previous table, the left number in each cell is the “return” to whoever is represented in the rows, in this case the husband, and the right number in each cell is the return to the wife (represented in the columns). Each one would like to obtain as high a return as possible. It can easily be seen that in this game there are two possible results that are in equilibrium: either to go together to the football game or to go together to the opera. The mathematics does not indicate which of these is the better choice.
The third game is a version of the common and familiar heads or tails. One player writes down his choice of heads or tails, without revealing his choice to the other player. The second player has to guess the choice of the first. If he guesses correctly the first player pays him, say, one dollar. If he guesses wrongly, he pays the other player one dollar. In this game the table looks like this
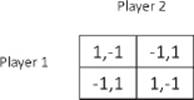
It can be proven quite simply that in this game there are no equilibrium strategies. This game is also called a zero-sum or fixed-sum game, as the payoffs merely pass from one player to the other. As can be seen in the table, the sum of the payoffs in each cell is zero, namely, the gain of one player is the loss of the other.
We have shown three games in one of which there was one equilibrium, in the second there were two equilibrium outcomes, and in the third, none. The explanation of equilibrium given previously still holds to some extent. For example, in the battle of the sexes, if the husband and wife agreed to meet at the opera, it would make no sense for one of them to arrive at the second performance without coordinating that in advance with the other. Game theory has no answer to the question of whether the opera or a football game is preferable; it does not rate the two options, per se. Neither does game theory recommend the adoption of an equilibrium strategy, even if it is the only one. Here is a table of a game that reflects this.
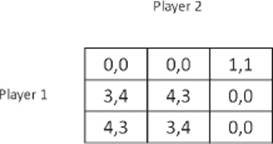
The numbers in the cells indicate, say, monetary payoffs. The strategy in which the first player chooses the upper row and the second player chooses the right column are the only ones in equilibrium, although it is clear that if the players restrict themselves to choosing the other rows and columns, the situation of both of them will improve, and moreover there will be no incentive for them to revert to their initial strategies.
Game theory developed another course of action for players in games presented in strategic form, and that is to use a mixed strategy, something that children do naturally when playing heads or tails. To prevent his rival from revealing whether he has chosen heads or tails, he flips a coin so that his choice is a random one. The mathematical expression of this is deciding not on a particular strategy but on a draw in which the chosen strategy is drawn according to the distribution of the chances that the player determines. In such a case what is the payoff? The actual result will be determined only once all the draws have taken place and it is then known which strategies were drawn in the lottery. At the decision stage the player knows only what lottery he has chosen, and likewise for the other players. For the purpose of deciding which lottery to choose, we determine that the outcome of the game will be the expectation (in the probabilistic sense) of payoffs, the expectation according to the chances that the players have determined. Although ultimately the player will receive the payoff that is the result of the various lotteries, the assumption is that at the stage of deciding on the lottery between the various strategies, the player is interested in achieving the highest possible expectation. We will examine this assumption in the next section.
As we noted, the concept of mixed strategies was introduced by Émile Borel, who also showed how to calculate such strategies in equilibrium for many instances of zero-sum games, but he did not believe that it was possible to solve all games in this way. John von Neumann, however, proved that in such games mixed strategies that were in equilibrium could always be found. The expectation of the payoffs is then the same in all the equilibrium states, independent of which equilibrium strategy is chosen, and that payoff is known as the value of the game. This is known as the minimax (or minmax) theorem, because the strategy minimizes the possible loss by each of the two players separately, leading to an equilibrium outcome. In the heads or tails game, the value is zero and the strategies selected by children, that is, to choose heads or tails with equal probabilities, are in fact in equilibrium. John Nash went further and proved that in every strategic game (that is a game in which every player has a finite number of strategies) there are mixed strategies that are in equilibrium.
If we adopt the possibility of mixed strategies, not only is it certain that an equilibrium exists, but in certain situations possibilities of reaching a more reasonable equilibrium arise. For example, we explained why the equilibrium in the 3 × 3 table above is not reasonable as a solution to the game, although it is the only equilibrium. If we allow mixed strategies, and assuming that the players want to maximize their expected payoffs, a new equilibrium comes to light. This is obtained when each player chooses one of the other options, that is, the two lower rows in the case of the first player, and the two left columns in the case of the second, with equal probabilities.
Note that by using mixed strategies we have moved from a situation in which a player receives an actual payoff, whether monetary, or the number of years in prison, or what have you, to a situation where the payoff is a lottery between several possible actual payoffs. In the next three sections we will discuss people's attitudes to states of uncertainty, and in particular to the use of lotteries.
Sometimes the suggestion to look for an equilibrium strategy causes unease, for example in the case of the prisoner's dilemma. On the abstract level we agreed that if a player has a dominant strategy he will use it. In similar day-to-day situations, however, we find it worthwhile to cooperate rather than to opt for the dominant strategy. The reasons for such a choice in normal daily life are not reflected in the limited model we presented. For example, our model does not take into consideration what friends of the suspect sentenced to years in jail are likely to do to the suspect who betrayed his partner in crime. This is a clear illustration of the fact that the mathematical game lacks very important elements that decision makers must take into account. Researchers were not unaware of this aspect, and they put forward models that take into account responses that are outside the table itself. One of the models allows an unlimited or unknown number of repeats of the game, so that every suspect will take into consideration future decisions of the other suspect, decisions that are likely to include retaliation for the current lack of cooperation. The analysis of such repeated games was one of the judges’ reasons in the citation awarding the Nobel Prize in Economics in 2005 to the mathematician Robert J. Aumann of the Hebrew University of Jerusalem.
The concepts of game theory have been included in other areas, such as economics, in which the distribution of resources takes place via markets that bring prices of the different products into equilibrium. Such a model was proposed by Kenneth Arrow, whom we mentioned earlier, and Gérard Debreu (1921–2004), a mathematical economist of the University of California, Berkeley, who was awarded the Nobel Prize in Economics in 1983.
As a result of these developments, the concept of equilibrium as well as other concepts developed in game theory, such as a zero-sum game, became part of general public discourse, although the participants in the discussion do not always draw the appropriate conclusions. For example, the incentives for people or companies to honor signed agreements are the punishments incurred if they breach the agreement, whether punishments are imposed by the courts, such as prison sentences or fines, or by future boycotts. In the absence of any retribution or expected punishment for infringement, an agreement is no more than a statement of intention, and it will be broken as soon as it is worthwhile for one of the parties to do so. Therefore, in cases where there is no system of punishment, as in many international agreements, it is up to the parties to the agreement to see to it that, as far as possible, the agreements themselves should have the property of Nash's equilibrium. In other words, no party to the agreement should benefit by breaching it unilaterally. Despite this elementary insight that originates from game theory, it does not appear that politicians who are signatories to agreements, sometimes fateful agreements, even try to take this into consideration.
The model we have analyzed is only one of a multitude of possibilities suggested by game theory to reflect and analyze circumstances in which decisions must be made either in confrontation with or in cooperation with other players whose interests might be opposed to ours. One fundamental model is of games in cooperative form. We shall not elaborate on this approach but will just say that here games are not determined by strategies that the players must take, but by the payoffs to coalitions that the players may form. Different formations of coalitions give rise to different allocations of, say, wealth. The theory studies, for instance, what would be stable outcomes, namely, outcomes that would not result in the disintegration of a given coalition; or how to measure the strength of a player based on the various coalitions he can join. The theory has been promoted to a great extent by John von Neumann and his colleague Oskar Morgenstern (1902–1977). They displayed much of the theory in the book Theory of Games and Economic Behavior, published in 1944. Many contributions to the theory of games in cooperative form have been added since then. It may be mentioned that von Neumann himself saw in this theory the right building block for a mathematical analysis of human behavior, parallel to infinitesimal calculus as the building block for the analysis of the physical world (in particular, he was not too fond of games in strategic form). It seems that in recent years games in strategic form were found to be more attractive; yet the cooperative game models, including market design relying on what cooperative game theory tells us (recall the aforementioned Nobel Prize to Alvin Roth) has not been abandoned and continues to be a fruitful field of study.
Mathematics plays a crucial role in analyzing the situations we addressed. Yet unlike the mathematics of the natural sciences, which can predict what is likely to happen, the mathematics of decision makers in a situation of conflict does not indicate what may occur, nor does it advise how to act. The current models are far from accurate depictions of the complexity of confrontations in real life. The product of this mathematics consists of proposed concepts or methods that will give the decision maker a better understanding of what confronts him. Sometimes mathematics may indicate a way to arrive at a criterion that expresses what is meant by “best for all.” In that case, mathematics may lead to the discovery of the best action. Mathematics may sometimes indicate what properties in the model limit the decision maker and, if possible, may lead to a change in the rules of the game. The mathematical analysis shown above is based on the assumption that the participants are rational and that they are acting to achieve the best, the best according to their subjective preferences, of course. Whether decision makers, either individuals or those making cardinal decisions at the national level, do in fact act in such a rational manner is a serious question that we will address in the next sections.