Mathematics and the Real World: The Remarkable Role of Evolution in the Making of Mathematics (2014)
CHAPTER VII. COMPUTATIONS AND COMPUTERS
53. THE MATHEMATICS OF COMPUTATIONS
The development of the electronic computer necessitated a change in the attitude toward mathematical calculations, and this resulted in the development of a new mathematical subject called computability theory or computational complexity. To understand the source of the change let us recall the method of logarithms discussed in section 51. The method was developed to simplify calculations. It converted multiplication into addition and reference to two tables. This conversion constitutes a great improvement for the human brain. What eases things for the human brain, however, is irrelevant for an electronic computer. For a fast computer, multiplication consists of repeated additions and is therefore a much more efficient operation than using logarithms. For a computer it is simpler and more efficient to carry out the multiplication directly rather than to calculate the logarithms and then add them. The fact that the process is based on elementary operations means that the crucial factor in determining the efficiency of a computation is the number of elementary operations required. To compare two methods of calculation by an electronic computer we need to compare the number of elementary operations that each method must perform to give the result of the calculation. But what is an elementary calculation? And how can we compare two methods or two programs developed for different purposes and different computers? It was the British mathematician Alan Turing who provided the appropriate framework for discussing these questions.
Alan Mathison Turing was born in London in 1912. His talent for and leaning toward mathematics were revealed when he was very young. He completed his first degree at King's College, London, stayed there as a fellow, and carried out research on the foundations of mathematics. He presented an alternative approach to Kurt Gödel's result regarding the theoretical limits of calculations, an approach based on a system that would later be called the Turing machine. In 1938 he received his doctorate from Princeton University, with Alonso Church (1903–1995) as his doctoral advisor. Church was a well-known mathematician whose research in mathematical logic dealt with similar topics but with a different approach. After returning to England, with the outbreak of World War II, Turing joined a team of scientists working for the Allies, trying to decipher the coded messages transmitted by the Germans. The team met at a place called Bletchley Park, which still today serves as a meeting place and as a museum of the history of computing. Within a short time Turing was in a central position in the deciphering efforts. With the help of an electromechanical computer available to the team, the Bletchley Park group succeeded in deciphering the German Enigma code, an achievement that played a significant part in the Allied victory. Turing had been declared a war hero by the wartime prime minister, Winston Churchill.
After the war Turing continued his research at Manchester University. He made an important contribution, which we will discuss later on, to a subject called artificial intelligence, attempted to build an electronic computer, and carried out research in different areas of biology. His work was cut short when he was accused of having relations with a young homosexual, which was then a criminal offence in Britain. Turing admitted to the charges and agreed to undergo chemical treatment to depress his sexual urge, offered as an alternative to a jail sentence. However, the social pressure together with the physical pressure from taking the treatment was apparently too much for him, and in 1954, two weeks before his forty-second birthday, he ended his life by cyanide poisoning. Many years later, in 2009, the British prime minister Gordon Brown apologized on behalf of the government for “the appalling way he [Turing] had been treated,” and in December 2013 Queen Elizabeth II granted him a rare “mercy pardon.” In 1966 the Association for Computing Machinery (ACM) instituted a prize in honor of Alan Turing, the prestigious Turing Award.
Before we present the main points of the theory of computability, we should state clearly that it does not presume to assess the efficiency of specific mathematical computing programs and thus to help the potential user to select a calculation method or program better than others. To do that the user needs to try the alternatives and to compare the practical results. Computability theory is a mathematical theory that tries to find the limitations of the capabilities of different algorithms. There is no reason to be alarmed by the terminology. An algorithm is simply a group or a list of instructions to be carried out. Thus, detailed directions on how to reach a destination B from point A constitutes an algorithm. A cookbook is a collection of algorithms whose objective is to prepare tasty dishes from the ingredients by following preset recipes. Operating manuals for different equipment are sometimes in the form of algorithms. How to add or multiply two numbers is generally presented as an algorithm.
A list of instructions as a way of performing mathematical calculations always existed, of course. The sieve of Erastothenes (mentioned in section 14) as a method of finding the prime numbers is an algorithm. The algorithm states that to find all the prime numbers from, say, 2 to 1,000, first delete all multiples of 2, that is, all even numbers greater than 2. From the remaining numbers delete the multiples of 3, that is, 9, 15, 21, and so on. Then, delete all multiples of 5, and so on, until all the non-prime numbers up to 1,000 have been deleted. At the end of the process, that is, when the algorithm has been implemented, only the prime numbers between 2 and 1,000 will remain. Thus, we have described an algorithm that finds the prime numbers between 2 and 1,000.
The word algorithm is a distortion of the name of the Arab mathematician Abu Ja’far ibn Musa Al-Khwarizmi, who lived in Baghdad from approximately 780 to 850 CE. He made many contributions to mathematics. He determined the digits for the numbers from 1 to 9 and was the first to designate 0 as a legitimate digit in the notation of numbers. He developed methods for solving algebraic equations. The word algebra is derived from the title of his book hisāb al-ğabr wa’l-muqābala (On Calculation by Completion and Balancing), in which he included methods for solving such equations. He made no less a contribution by translating and in the spirit of the time, corrected and improved, the writings of the Greek mathematicians, and he thereby deserves the credit for playing a major role in and being largely responsible for the preservation of those important texts.
We have already said that the efficiency of different algorithms is assessed by comparing the number of elementary operations that they implement. Yet the questions remain: What is an elementary operation, and how can algorithms with completely different purposes be compared? That was the purpose for which the Turing machine was devised. It is not a machine in the usual sense of the word, using electricity or other fuel, producing smoke, and requiring maintenance from time to time. The Turing machine is a virtual machine, meaning it is a mathematical framework (and there are several versions of this framework). The machine receives input, an ordered finite number of symbols, or an alphabet, marked on a tape. The tape is not limited in length. The machine can be in one of several predetermined states. The machine has a “reader” that can identify what is written in one of the cells on the tape. As a result of what it reads, the “program” of the machine causes a change in the machine's state according to a predetermined rule, a change in the letter in that cell to another letter, also in a predetermined manner, and a move to read the letter in the adjacent cell, again according to a predetermined rule. Such a program creates a series of moves from cell to cell, possible changes to the letters written in the cells, and possible changes in the state the machine is in. These operations are the elementary operations that will enable algorithms to be compared. The algorithm ends when the reader reaches a cell with a prescribed symbol. The result of the algorithm is defined by the state the machine is in when it stops and what is written on the tape at that time.
What is surprising is that every calculation imagined until now, whether a numerical calculation, finding the minimal distance for a journey between two towns, or finding the meaning of a word in a dictionary, all these can be translated into the mathematical framework of this hypothetical, virtual machine. In other words, a Turing machine can be programmed by its letters and the rules for moving from cell to cell to perform the calculation. The emphasis is on “an acceptable calculation,” meaning every imaginable calculation can be translated into a calculation on a Turing machine. That is a “thesis,” known as the Church-Turing thesis, and not a mathematical theorem. So far no discrepancies have been found in this thesis.
We have stated that the efficiency of algorithms is compared via the number of elementary operations they perform on a Turing machine to achieve a desired outcome. We will repeat our warning, however, that the comparison that interests the computability-theory experts is not between two methods of finding, say, the prime numbers between 2 and 1,000. With such a definite objective, it is incumbent on the high-speed computers to find the solution that will be to our satisfaction. The comparison of main concern between two algorithms will be between their performance when, in our example, the upper limit is not a fixed number, say, 1,000, but a general number, N, where Nbecomes larger and larger. Obviously the larger N becomes, the larger will be the number of steps the algorithm will have to perform to find the prime numbers. The comparison between the two algorithms will be between the rate of increase in the number of steps in each algorithm as N increases.
We will explain now what is meant by the term their rate of increase as N increases. If the expression describing the number of steps required to solve the problem is given by an expression of the following form,
N2, or 8N10, or even 120N100,
we say that the rate of increase is polynomial, that is, an expression that is a power of N. If the expression giving the number of steps required is of the form
2N, or 1204N, or even 104000N,
the rate of increase is exponential. The names reflect how the parameter appears in the expression.
Despite the fact that for a given algorithm there is a difference between a rate of N2 and N3, computational complexity theory experts put them together in the polynomial rate category, and similarly with the exponential rate. The class of problems that can be solved by algorithms that reach the result of the calculation at a polynomial rate is called class P.
Here there is another interesting distinction, as follows. In many cases it is far easier to check whether a proposed solution to a problem is correct than to find the solution itself. For example, in sudoku there is a 9 × 9 square with numbers between 1 and 9 appearing in some of the smaller squares. The object is to complete the entire grid such that every row and every column and every 3 × 3 sub-square of the nine that make up the whole table contains all the digits from 1 to 9.
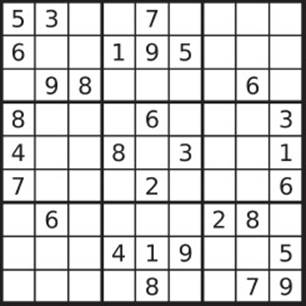
Image from Wikimedia Commons/Tim Stellmach.
The objective of finding the solution, that is, filling all the empty boxes so that each row, column, and so on contains all the digits from 1 to 9, is likely to be difficult and to require many attempts. Yet when someone suggests a solution, it is a simple matter to check whether it is correct. Here too the computability experts are not interested in the number of steps needed to discover whether the proposed solution to a 9 × 9 sudoku is correct or not. They are interested in the number of steps required to check a sudoku whose size keeps increasing, in other words, sudoku of size N × N, when N keeps rising, and in the rate at which the number of steps increases. (A sudoku in which arbitrary N numbers have to be arranged still uses an input with a finite number of symbols, as every natural number can be represented, for example, as a decimal number that uses only ten symbols.)
We quoted sudoku purely as an example. The difference between finding a solution and checking a proposed solution arises in many algorithmic tasks; we have already mentioned (in section 36) the public competitions for solving equations. To solve equations is hard. To check if a solution is correct is, in most cases, easy. Also, in checking solutions, a distinction can be drawn between a polynomial rate and an exponential rate. The class of problems for which proposed solutions can be checked using algorithms that suffice with polynomial rates of increase in the number of steps required is called NP (the letter N is derived from the term non-deterministic, as the check can be performed simultaneously on all the proposed solutions).
Now here is a chance to win a million dollars. The experts in computability theory do not know if the two collections of problems, those in class P and those in class NP, are the same or different. (It can be proven that every problem in P is also in NP, in other words, if it can be solved at a polynomial rate, then the proposed solution can also be checked at the same rate.) At the beginning of the third millennium the Clay Mathematics Institute in Providence, Rhode Island, published seven unsolved problems in mathematics and offered a million dollars for the solution of each one. The question whether P = NP is one of those questions. sudoku, for example, is in the NP class. If you can prove that every algorithm for solving N × N sudoku, with N rising necessarily, requires a number of steps that depends exponentially on N, you will receive a million dollars (provided you do so before anyone else does).
The discussion of P and NP classes is just one example of the many questions that the mathematics of computation deals with. For example, computability experts showed that if you present a polynomial algorithm to a sudoku problem, then for every problem in the NP class there is a polynomial algorithm (in particular, if you do that you will have solved the problem of the equality of P and NP, and you will receive a million dollars). Such problems, the polynomial solution to one of which implies that every problem in the NP class has a polynomial solution, are called NP-complete. Research in computability has so far identified a very large number of NP-complete problems.
The research is also involved in seeking efficient solutions to specific problems, or in proving that there are no efficient solutions to other specific problems. For instance, just a few years ago, in 2002, a polynomial algorithm was presented for checking whether a given number is prime. We will expand on this question in the next section. Another question that has far-reaching implications that we will discuss in section 55 is whether there is an efficient algorithm for finding the prime factors of a number that is the product of two prime numbers. The efficiency characteristic becomes even more precise, for instance, in identifying problems whose solutions require a number of elementary operations that are not larger than a linear expression of the size of the input, that is, an expression of the type aN for a given number a, or an expression that is a product of the type Nln(N), that is, linear in N multiplied by the logarithm of N. The latter is a slower rate than quadratic, and hence preferable. Hundreds of problems have been examined and the degree of efficiency of their possible solutions has been identified. Many problems are still unsolved; in other words, the rate of increase in the number of steps required to solve them has not yet been identified.
The question arises whether the abstract discussion of the number of steps required to solve a problem with an input of size N with N increasing is relevant to finding a solution to real problems that interest the users of the computer. No one in his right mind intends to try to solve a sudoku of size one million by one million, let alone of size N, as N tends to infinity. The answer is surprising. There is no logical argument that relates the rate of increase in the number of steps required as N tends to infinity to the number of steps required to solve real problems. Moreover, there are problems in class P that theoretically can be solved efficiently but in practice cannot be solved by today's computers in a reasonable time. Nevertheless, many years of experience have shown that, in general, intuition gained from questions with a parameter that tends to infinity also applies to versions with a large but finite parameter.
This is an appropriate point to discuss the difficulty and validity of intuition rooted in various algorithms and in the way computers work. As an algorithm is a series of instructions, it is easy for the human brain to understand, implement, and even develop intuition about how the algorithm works. Associative thinking, which is the basis of the human thought process, is founded on the approach of deriving one thing from another, a process analogous to an algorithm. The same applies to the computer. It is easy for very young children and youngsters to master the handling of a computer, and they even relate to it intuitively. Not infrequently, if you ask for help related to the working of your computer from someone with computer experience (not necessarily an expert), the answer will be, “Let me sit at the keyboard and I'll find out what to do.” Sitting at the keyboard activates the associative reactions, the intuition. It is often assumed that this is age-related. I do not think it is. To use the necessary intuition apparently requires you to overcome the psychological barrier, a barrier of fear perhaps, regarding the new machine, to operate it, which seems superficially to be an impossibility. Adults are challenged by this barrier, not youngsters who are growing up in proximity to computers. Nevertheless, at least two difficulties along the route to an intuitive understanding of the computer should be acknowledged. First, as mentioned, the incomprehensible speed of the computer clashes with human intuition, the latter of which developed in an environment where changes occur much more slowly (although it will be easier for the generation born in the computer age to develop such intuition). Second, the computer itself does not “think” associatively. The computer, at least the computer of today, does not think the way humans think. It carries out very precise instructions, coded in the software, and sometimes logical operations are incorporated in the software instructions. To develop intuition about logical arguments is a difficult or even impossible task. Which is why one will come across reactions from even the most experienced experts such as, “I don't know what the computer wants.”