Mathematics and the Real World: The Remarkable Role of Evolution in the Making of Mathematics (2014)
CHAPTER I. EVOLUTION, MATHEMATICS, AND THE EVOLUTION OF MATHEMATICS
7. AND THEN CAME THE GREEKS
Greek mathematics that developed in what is called the classical period, between about 600 BCE and the rise to power of Alexander of Macedon (i.e., Alexander the Great) in the fourth century BCE, reflected dramatic changes in the approach to mathematics and in the methods of development, analysis, and uses of mathematics. The method formulated in that period served the Greeks themselves in the next few centuries and has remained, almost without change, the dominant system of mathematics until the present. Before we give a brief description of the developments, we should observe that after two thousand five hundred years of learning and using the method introduced by the Greeks, and generations during which we have become accustomed to such a system of analysis and debate, it is sometimes hard to appraise the significance of the dramatic turnaround that took place then. Today, the path paved by the Greeks seems natural and self-evident, but the new ideas are in contrast to what was expected from development in which evolutionary fundamentals were predominant. Greek mathematics constituted a sharp deviation from thousands of years of earlier mathematical activity and put forward an approach that largely contradicted the path dictated by healthy intuition. It is therefore understandable why the process of familiarization with the new ideas, and the development and incorporation of the method itself, took hundreds of years. This section deals with this aspect of the main developments. The next section will discuss what motivated the Greeks to instigate this revolution in mathematics.
In contrast to the Babylonian and Egyptian periods, we have no original writings from the classical Greek period. At that time writing was done with ink on papyrus, a method learned from the Egyptians, but the papyri did not survive. We learn about the development of mathematics in the classical period from comments found in much-later writings and from later versions of the ancient texts. Although those versions are copies of the original ancient texts, the practice at that time did not require the scribe to copy exactly, and he felt free to insert or omit texts, to correct errors (and to cause new errors), and so on, all in accordance with his understanding of the material. Even the most famous book on mathematics, Euclid's Elements, is known to us via versions copied hundreds of years after Euclid. Historical research of that period is based wherever possible on comparisons of later texts, copies of earlier texts made by various scribes. Although the picture we obtain is not a detailed one, it seems to be complete and reliable.
Thales of Miletus (in what is today Turkey) and his successors and disciples Anaximander and Anaximenes, also from Miletus, are credited with having started the reform. Information on Thales (640–546 BCE) comes from later sources. Plutarch, who lived in the first century CE, wrote of Thales that he was the first philosopher who was not a politician. Elsewhere it is written that Thales was the first to use his wisdom for practical purposes. It is not clear how we today should understand these statements, but it seems that Thales became very rich from trading. He traveled extensively in the ancient world, learned from the Babylonians and the Egyptians, and spent several years in Egypt. He became famous as a result of measuring the height of the pyramid in Giza. The method he used was to wait until the shadow of a rod was equal to its height, and then, using the similarity of the triangles (i.e., the properties of similar triangles) he claimed that the shadow of the pyramid was equal to its height. As he could measure the length of the shadow directly, Thales was able to arrive at the height of the pyramid. Based on this, he developed the geometry of similar triangles and used it to calculate the size of ships and their distance from the shore. He did not stop there. He proved that all triangles with the same length of base and the same two angles from the base are congruent. The Babylonians, Chinese, and Egyptians performed similar operations, but none of them found it necessary to formulate a general theory relating to geometric shapes or to prove that their method of calculation alwaysgave the correct result.
Whether Thales was the first to introduce the concept of proof or whether it was attributed to him later, its revolutionary impact cannot be overstated. If you have been convinced that a certain assertion is correct, it would be a waste of time and resources to go back and prove it rigorously, especially if you try to prove that it always holds. Unproved propositions may be erroneous, but to exclude errors categorically requires an effort whose utility is not generally justified. The requirement for absolute proof would be an encumbrance in the evolutionary struggle. There was a reason that throughout thousands of years of the development of mathematics before Thales, mathematicians did not try to prove propositions they were convinced were correct. However, after Thales had taken the first step and Greek mathematicians in subsequent generations had followed his path, the concept of proof became a cornerstone of mathematics.
Other crucial milestones in the formulation of the new concepts in mathematics were the contributions by Pythagoras and his school. Pythagoras came from the island Samos, not far from the coast of Italy. According to the tradition, he was born, so it is believed, in 572 BCE, and it is generally thought that he was a pupil of Thales in Miletus. He went to study in Egypt, and when he returned to Samos he found a regime of tyrants and left for the town of Cortona in Italy, which was then under Greek rule, and founded the Order of Pythagoras. All sorts of mysteries have been attributed to that order, and it is difficult to separate truth from myth. It was involved in local politics in Cortona and considered itself part of the elite or upper stratum. It thus came into conflict with the democratic regime that came to power in the town, and, according to popular history, Pythagoras himself was murdered in 497 BCE. The members of the order dispersed, joining various seminaries in Greece, but they continued with their mathematical activities according to the Pythagorean tradition for about two hundred years. They customarily attributed every important theory or mathematical result to the founder of the order, so it is not clear what Pythagoras's own contributions were and what should be attributed to his followers.
One of Pythagoras's best-known contributions to mathematics is the theorem named after him: in a right-angled triangle, the sum of the squares of the sides equals the square of the hypotenuse. This is one of the most famous mathematical theorems, and until now, hundreds of different proofs of it have been published. Beyond the discovery of the general property in the theorem, Pythagoras's main contribution in this case was his search for a general property. As we saw above, the Babylonian's knew about Pythagorean triangles, that is, triangles with sides whose lengths were natural numbers that satisfied the theorem, and they made a list of such. The Chinese left written instructions on how to calculate the length of a side of a triangle if the lengths of the other two sides are known, and they gave many numerical examples and illustrations of various such triangles. Calculations left by the Egyptians show that they too knew of the relation of the lengths of the sides of a right triangle in many examples of specific triangles. It did not occur to any of them to even ask whether the property applied to all right triangles or to prove Pythagoras's theorem even for those triangles for which they had calculated the figures. They knew about the connection between the lengths of the sides, but they used it only in the context of specific calculations.
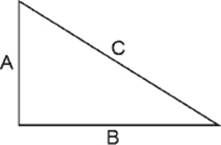
Moreover, Pythagoreans (and possibly Pythagoras himself) did not merely prove the relation between the sides of the triangle but looked for, and found, a formula according to which all Pythagorean triangles can be calculated.
The formula is (in the notation of today): for all two natural numbers u and v, such that u is bigger than v, define
A = 2uv, B = u2 – v2, C = u2 + v2.
A simple calculation shows that A2 + B2 = C2, or, in other words, A, B, and C are the sides of a Pythagorean triangle. The Pythagoreans proved that all Pythagorean triangles are obtained in this manner (the claim that these constitute all the triangles appeared in Euclid's book, but without a proof).
Note the conceptual leap. The Babylonians and the Chinese compiled lists of many Pythagorean triangles; the Greeks found a proof that included all of them. The Babylonians made a great effort to discover Pythagorean triangles but did not think of trying to find a formula that would calculate all of them. Why, indeed, should anyone try to find all those triangles? What evolutionary advantage would be expressed by the desire to find all the numbers?
A major conceptual contribution of the Pythagoreans is related to the method of proof. In the next chapter we will discuss the connection between the Pythagoreans and their view of the world. At this stage we will note that they believed in the close link between numbers and geometry, and that the world consists of natural numbers and their ratios, that is, fractions, or in the language of the Greeks, sizes that can be expressed. To their great surprise, so it is told, they discovered that there are sizes that cannot be expressed, or in our terminology, irrational numbers. An example of such a number is the length of the diagonal of a square, the sides of which measure 1. According to one account, the Pythagoreans kept this revelation secret and threw their colleague Hippasus, who had leaked the existence of such numbers outside the Pythagorean school, into the sea. Another version of the story is that it was Hippasus himself who discovered the existence of irrational numbers and that he was thrown into the sea because of heresy, as his discovery destroyed the basis of belief in the structure of the world. One way or the other, what interests us is the following step-by-step proof of the hypothesis.
a. Consider a triangle consisting of two sides of a square with sides length 1 and its diagonal.
b. According to Pythagoras's theorem, the length of the hypotenuse is the square root of 2, denoted by √2.
c. Let us assume that the hypothesis is not true, that is, √2 it is a rational number; in other words, it can be written as a fraction or the ratio of two positive whole numbers, say ![]() .
.
d. We can assume that either the numerator or the denominator is odd (because if they are both even, they can be divided by 2 until one of them is odd).
e. Now square the ratio ![]() , and according to the hypothesis this is equal to 2, leading to the equation a2 = 2b2.
, and according to the hypothesis this is equal to 2, leading to the equation a2 = 2b2.
f. Hence a is an even number, which can therefore be written as 2c.
g. Substituting 2c for a in the previous equation gives 4c2 = 2b2.
h. Dividing both sides by 2 leads to the conclusion that b is also an even number.
i. But we specified that a and b are not both even. We have reached a contradiction, derived from the assumption that √2 is a rational number.
j. Conclusion: assuming that √2 is rational leads to a contradiction; hence √2 cannot be written as a fraction, and it is therefore an irrational number.
This type of proof is known as reduction ad absurdum. An argument that made use of contradiction was not only exceptionally innovative in its time, but it also runs counter to the natural way in which the human brain works. How could a claim that starts with the words “Assume that X is not…” be developed? The reader is invited to try to remember when and where, apart from in mathematics lessons, he or she intuitively used a thought process that assumed that something did not exist. Intuitive thought is founded on association, on links between current observation and the recognition of previous situations. A nonexistent event does not naturally arise as an association. After so many years of mathematical developments it is hard to assess how revolutionary this approach was. The real reason for the Pythagoreans hiding the discovery of irrational numbers may have been that they were not completely sure of the validity of proof via reduction ad absurdum. The uncertainty concerning such proofs reappeared in modern times, and we will discuss it in the chapter on the foundations of mathematics.
The Pythagoreans were familiar with prime numbers, that is, the natural numbers that can be divided without a remainder by only themselves and 1, and they studied them extensively. Apart from anything else, the Greeks proved that the number of prime numbers is infinite. The proof is simple.
a. First, note that every number can be expressed as the product of prime factors of the number.
b. Multiply n prime numbers and add 1 to the product. We get a number that we denote by M.
c. If M is a prime number, we have found one not among the n prime numbers that we had started with.
d. If M is not prime, consider a prime factor of M.
e. The prime factor can be divided into M without a remainder, hence the prime factor of M is different from each of the n prime numbers we started with as these, when divided into M, give a remainder 1.
f. Thus, in the second possibility (i.e., step d), we also found another prime number in addition to the n numbers that we multiplied.
g. We have thus shown that there are more than n prime numbers. But n is an arbitrary number, therefore the number of prime numbers is not finite and the proof is complete.
But why should anyone be interested in the question of whether the number of prime numbers is infinite? Where in evolution would the question whether there is an infinite number of any particular object be a meaningful question? Interest in the mathematical properties of prime numbers, including apparently useless properties, started with the Greeks, continued throughout generations of mathematicians, and is still today an important part of mathematical research. In current times uses of prime numbers have been discovered apart from the abstract mathematical interest, including commercial uses such as encoding, which we will discuss further on. For thousands of years the interest was purely mathematical. For the Greeks, however, it seems that the involvement in numbers was not simply motivated by curiosity but by the belief that thus they would better understand the world around them.
The next leap in the amazing change wrought by the Greeks in the development of mathematics is attributed to the Academy of Athens and its disciples, and in particular to its founder, Plato, his friend Eudoxus, and Plato's pupil Aristotle. The conceptual contribution of this group may be summarized as the formulation of the approach that bases mathematics on axioms and on logic as the essential tool in the system of deductive proof. As we will try to establish here and later in this book, these two contributions conflict with the natural intuition of human thought.
Plato (427–347 BCE) came from an aristocratic and influential family. He was a pupil of Socrates, who is considered the father of general and political Western philosophy. In his youth, Plato entertained political ambitions, but he abandoned them, perhaps because he saw what happened to Socrates, who was sentenced to death for his opposition to and criticism of the rulers of Athens. Plato traveled widely in the ancient world, visiting Egypt and the Greek colonies in Sicily, where he became acquainted with Egyptian mathematics and the Pythagoreans. On returning to Athens, he founded the first academy in the Western world. The academy had a decisive influence on contemporary science and philosophy. Plato was essentially a philosopher, and his interest in mathematics stemmed from his belief that the truth about the nature of science can be revealed only via mathematics. On the entrance of the academy he inscribed “Let none but geometers enter here.” Plato went further and, in accordance with the philosophy he developed in other fields, claimed that mathematics, or mathematical results, have an independent existence in the world of ideas that are not necessarily related to the earthly reality that we experience in daily life. Specifically, we do not invent mathematical results; we discover them. The right way to do this is to formulate the assumptions, which we will call axioms, and to use them to draw mathematical truths from them using deductive logic. To this end the axioms should be simple and self-explanatory. The smaller the number of axioms, the better. In modern mathematics it is generally accepted (admittedly, not by all researchers) that the researcher can choose his axioms freely. It is doubtful whether Plato would agree. He believed that the axioms are the link between man and mathematical truth, and they must therefore be “correct.”
Formulating axioms and examining the situation under prescribed assumptions is today an accepted method of analysis not only in mathematics but also in many other fields. We should be aware, however, that this method is contrary to natural human thought. It is difficult to understand how evolution gives an advantage to someone who says, “I cannot see a tiger nearby and so I assume there is no tiger in the area.” What benefit will accrue for someone who ignores certain attributes just because he has not assumed them? Even mathematicians reared on the system based on axioms cannot limit their intuition to axioms. First, they solve the problem confronting them intuitively, or guess how to solve it, and only then do they check whether their solution was based solely on the axioms or also on additional assumptions or on properties not consistent with the axioms. In the latter case they must look for another solution.
In Plato's time great emphasis was placed on abstract mathematical problems such as squaring the circle, dividing an angle into three equal angles, or doubling a cube (i.e., calculating the edge of a cube whose volume is double that of a given cube), and all these using only a ruler and a compass. In other words, they were attempting to draw a square with the same area as a given circle, using only a ruler and a compass, and likewise with the other problems.

These problems were known before Plato. The problem of squaring the circle is attributed to the philosopher Anaxagoras, who thought about it while in prison, charged with impiety. The problems received even greater attention in the time of Plato, and this was at the same time as efforts were made to base mathematical proofs on as few assumptions as possible. The answer to the problems was that it is impossible to perform those tasks with just a ruler and a compass. The complete proof was not obtained until the nineteenth century. These and similar problems motivated research from the time of the Greeks until today.
The question arises, what made the Greeks interested in these questions? One story ascribes the problem of the doubling of the volume of a cube to a Greek ruler who was envious of his counterpart in a neighboring city and asked the builders of a mausoleum in that city to build one for him with double the volume. The story is not very convincing. No reasonable ruler would restrict his builders to the use of only a ruler and a compass. The origin of the idea not to use all the means available does not lie in the evolutionary struggle. Imagine ancient man fleeing from a tiger and thinking, “I wonder if I can run away on one leg only.” Such individuals would not survive. Another version of the source of these problems is found in the writings of Plutarch. According to this story, the inhabitants of the city of Delos asked the local oracle for advice as to how to stop the constant disputes among themselves. The oracle's answer (not surprising, it may be said) was that they should double the volume of Apollo's altar in the city. The inhabitants asked Plato how to do this, and he, arguing that the oracle doubtless had proper mathematical intentions, interpreted the oracle's instructions to mean they should build with the use of just a ruler and a compass (also not surprising, as Plato wanted to promote his method). The point is that whichever version one prefers, questions that apparently do not relate to practical problems have occupied mathematicians since then.
Eudoxus (408–355 BCE) was born in the Greek city of Knidus on Cyprus and studied under the Pythagorean mathematician Archytas. Eudoxus traveled to Egypt to study and in 368 BCE joined Plato's academy in Athens. Eudoxus made many contributions to astronomy and mathematics. Here we will concentrate on only some of his significant contributions to the philosophy and practice of mathematics. Two of his innovations derived from his study of irrational numbers. Already in his time, many geometric dimensions were known that could not be expressed as a ratio of two integers (Plato had shown that the square roots of the prime numbers up to 17 were irrational numbers). Today we refer to both rational and irrational numbers as numbers, but in those days it was not clear in what sense irrational numbers were numbers. Eudoxus developed a mathematical theory that drew a distinction between numbers used to count individual elements (today referred to as natural numbers) and their ratios on the one hand, and numbers that measure geometrical lengths on the other. According to Eudoxus, mathematical operations in the two systems have different meanings. The interpretation of operations like addition, multiplication, and so on, on geometrical dimensions, is geometric. For example, multiplying √2 by √3 expresses the area of a rectangle with sides of lengths √2 and √3. With regard to natural numbers, Eudoxus defined the ratio of two numbers, say n divided by m as the number of times m goes into n, and the product of two numbers, again say n and m, as the result of counting n elements m times. The result of this distinction was the separation of geometry from algebra or arithmetic, a separation that was bridged only in the seventeenth century by René Descartes. It is interesting to note that even today we use the geometric concept of “square” to express a number multiplied by itself. The need to distinguish between two types of numbers resulted in Eudoxus's using concepts that still today are considered the foundations of mathematics, that is, definitions and axioms. He defined rational numbers, a point, a line, length, and so on, and formulated several axioms precisely. This was apparently one of the first attempts to present precise definitions and axioms.
The need to give exact definitions is not a natural one. In discussions between humans, it is sufficient to reach a situation in which the participants know what is being discussed, and it is not necessary to waste time on exact definitions of the topic under discussion. To invest time and effort in defining what is a point, a length, or a plane, when everyone knows what these terms mean, seems superfluous. The process of making a definition, apparently, seemed unnecessary also during the thousands of years of mathematical development prior to the Greeks, but it did not seem so to the academicians of Athens, and mathematics inherited the practice from them and has preserved it until today.
Another contribution made by Eudoxus, essentially technical, is known as the method of exhaustion. This was an extension of a development by the Pythagoreans, who, after discovering that irrational numbers cannot be expressed by means of natural numbers, showed that they can be approximated by ratios of natural numbers. Eudoxus developed a system for calculating areas enclosed by general curves, such as a circle, by removing the areas within them, such as rectangles or other shapes whose areas are simple to calculate, until the total area to be calculated is “exhausted.” Thus the area can be calculated by a close approximation. Eudoxus was very close to the concept of a limit, but he did not actually reach it. That was developed many years later by Archimedes, and is still used today as the basis of differential and integral calculus. Over and above the intrinsic technical contribution of the exhaustion method, the very presentation and formulation of the general method was itself an important contribution.
The third in the honor roll of the academy of Athens was Aristotle, a pupil of Plato. Aristotle was born in 384 BCE in a city close to Salonika, the capital of Macedonia, and, like Plato, came from an aristocratic family. His father was court physician to the Macedonian king Amyntas. At an early age Aristotle moved to Athens and became a pupil of Plato. Toward the end of Plato's life, or after his death (it is not clear enough which), Aristotle left Athens and founded the Royal Academy in Macedonia. His departure from Plato's academy was apparently the result of a difference of opinion over the scientific direction the academy was taking, and his decision may have been influenced by the fact that he was not appointed to be Plato's successor. He was also concerned about persecution by the Athenians, who considered him a Macedonian, then an enemy of Athens. He founded the Royal Academy of Macedonia, where he also taught Alexander the Great, who became the most prominent figure in the world of that time. Later Aristotle returned to Athens, where he founded his own academy, the Lyceum; its remains can be seen in Athens today. After Alexander's death, the Athenians accused Aristotle of supporting Macedonia, making him flee again. He returned to Macedonia, where he died in 322 BCE.
Aristotle's main contribution to the new mathematics was in the development of logic as a tool for analysis and for drawing conclusions. Syllogisms formulated by Aristotle still serve as the basis of logic. After such a long time, we are so familiar with these rules that their formulation seems simple, correct, and indisputable. We will claim that some of those rules, even if it is easy to agree with them via orderly thought, are not consistent with intuitive thought or with spoken language that developed naturally. We will deal with some of those rules now.
Following the generally accepted practice, we will use letters, say P or Q, to signify a claim or a statement. We will sometimes abbreviate. For example, “P implies Q” means “In every case, if P holds, then Q must hold” (in mathematics the terminology “In every case, if P is true, then Q must be true” is used). Similarly, we will sometimes write “P” when we mean that P holds (or is true), and we will sometimes write “not P” when we mean that P does not hold (namely, P is false).
The first rule is known as modus ponens, which is an example of an intuitive logical claim that may be reasonably assumed to be supported by reason as the result of evolution. The rule is as follows:
If P implies Q
and if P holds
then Q holds.
The following is such a claim: if it is raining, the sidewalk is wet; it is raining now, so the sidewalk is wet. The claim is an intuitive one because in the daily life of every living being, however inferior it may be, there are indications that this relation holds. The Pavlov effect is of the modus ponens type: the ringing of a bell implies that food has arrived. From this to mathematical inferences of the modus ponens type is not far, as we have seen with the animal and human examples cited above.
The next syllogism, the modus tollens, is different. It reads as follows:
If P implies Q
and if Q is false
then P is false.
The following is such a claim: if it is raining, the sidewalk is wet; the sidewalk is not wet, so it is not raining now. From a mathematical logic aspect the claim is correct, like the previous one. Yet it is much harder for the brain to absorb. The reason for the difficulty lies in the statement that an event is nonexistent. It is much easier for the brain to accept intuitively that an event occurs and to draw conclusions from it. To draw conclusions from an event that has not occurred is much harder. Many events do not take place, and evolution has not taught the brain to scan those nonexistent events and to draw conclusions from them.
Clearly we must differentiate between two types of negative that appear the same. “The sidewalk is not wet” is translated in the mind as “the sidewalk is dry,” but it is easier to conclude that it is not raining from the claim that the sidewalk is dry than it is to draw the same conclusion (it is not raining) from the claim that the sidewalk is not wet. We can derive a recommendation from this for anyone speaking or trying to persuade someone of something: steer clear of arguments based on “not.”
The difficulty in applying the syllogisms intuitively has been recognized by logicians, and they developed techniques to identify such errors, or syllogistic fallacies. Here is one example of the many that are available. A person declares the following:
No well-bred person reads tabloids.
I do not read tabloids.
He intends to imply that he is a cultured person. Many would agree, intuitively, at least. But the conclusion is not a logical consequence of his statements.
The connection between these two syllogisms is inherent in the following two rules, also formulated by Aristotle. The first is called the law of excluded middle:
Every proposition P either holds or does not hold, that is, P is either true or false.
The second is the law of contradiction:
A proposition cannot be both true and false, that is, P and not P cannot coexist.
The proof via reduction ad absurdum discussed above, and which, as we stated, is difficult to understand intuitively, is based on these rules. We want to prove P; we show that by assuming “not P” we arrive at a contradiction, so we can conclude that P holds. It sounds simple, and with a calm and well-ordered analysis the proposition is simple, but the use of this principle intuitively is by no means simple. What evolutionary advantage would a living being obtain from developing this principle intuitively? As will be seen below, the law of excluded middle will play a vital role in the study of the foundations of mathematics in the twentieth century.
Aristotle made other contributions to mathematics, physics, and philosophy, some of which we will describe later in this book. Here we will refer to his involvement in the concept of infinity. The concept of infinity did not appear in any earlier civilizations. When they referred to the term infinity, they meant a collection of elements too large to be counted or contained. The concept of infinity did however greatly intrigue the Greeks, especially in connection with the physical structure of the world and how long it had existed. Zeno, following his teacher, Parmenides, alludes to infinity in his paradoxes. We refer to the dichotomy paradox in section 51 and here only recall that the paradox states that a person who wishes to get somewhere would never reach his target, as he has to cover first half of the distance, then one-quarter of the distance, then one-eighth, and so on, in an infinite number of steps. Following this alleged paradox, Aristotle developed an elaborate theory of infinity that we do not describe here as it does not pertain to mathematics. Its contribution to mathematics was to distinguish between potential infinity and an infinite collection of elements. Potential infinity in Aristotle's terminology refers to finite collections of unlimited size, such as increasing finite collections of prime numbers. He drew a distinction between these and a set of infinite size. The latter type of infinity was not an acceptable mathematical concept, amenable to logical manipulations. Thus, according to him, the question “Are there more prime numbers or more even numbers?” is not a legitimate question. The study of these concepts was renewed by mathematicians in the nineteenth and twentieth centuries.
The contribution made by Greek mathematics in the classical period was summarized by Euclid. Not much is known about Euclid's life. He lived around 300 BCE and may have studied in the academy of Athens, but he carried out most of his work in Alexandria in Egypt. He was one of the founders of the famous academic center in that city. Although Euclid was active after the classical period, his main mathematical work (which consisted of thirteen volumes), known as Euclid's Elements, presented in an orderly and detailed fashion the mathematical knowledge developed in classical Greece. In addition, the Elements organized, established, and disseminated the novel approach developed at that time. Over and above the impressive collection of mathematical findings, the development was based on definitions, axioms, deductive proofs, and defined syllogisms. There are no copies left of the Elements that were actually written in Euclid's time. All the versions found (the earliest of which, fragments only, are from the first century CE, i.e., about four hundred years after Euclid; the oldest dated full version is from the ninth century CE) contain remarks, amendments, and additions by those copying the book. From a comparison of the different versions we can nonetheless conclude that Euclid himself organized and arranged the book according to the different subjects, gave the definitions, established his methods of proof, and laid the foundations of the whole approach. It is no wonder that the Elements became one of the most widely distributed books in the world of all time and that it has apparently been translated into more languages than any other, except for the Bible.