SAT SUBJECT TEST MATH LEVEL 1

TOPICS IN ARITHMETIC

CHAPTER 4 Ratios and Proportions

PROPORTIONS

A proportion is an equation that states that two ratios are equivalent. Since ratios are just fractions, any equation such as in which each side is a single fraction, is a proportion. The proportions you will see on the Math 1 test always involve one or more variables.

Often one of the first few questions on a Math 1 test will require you to solve a proportion. You should always do that by cross multiplying. Later, more difficult questions might require you to work out a word problem by first setting up a proportion and then solving it.

EXAMPLE 3: If then

20(x + 3) = 19(x + 5) 20x + 60 = 19x + 95 x = 35

EXAMPLE 4: What is the length of in the figure below?

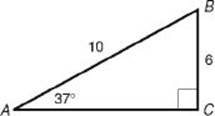
Since the measures of the angles in the two triangles are the same, the triangles are similar. Therefore their sides are in proportion. (See Chapter 9.)

NOTE: In Chapter 14, you will read about the trigonometric ratios and see that

A rate is a fraction that compares two quantities measured in different units. Rates often use the word “per” as in miles per hour and dollars per week.

EXAMPLE 5: Frank can type 600 words in 15 minutes. If Diane can type twice as fast, how many words can she type in 40 minutes?

Since Diane types twice as fast as Frank, she can type 1,200 words in 15 minutes. Now handle this rate problem exactly as you would a ratio problem. Set up a proportion and cross multiply:

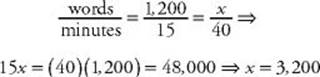
Occasionally on the Math 1 test rate problems involve only variables. You handle them in exactly the same way.

TIP

A rate can always be written as a fraction.

EXAMPLE 6: If a apples cost c cents, find an expression that represents how many apples can be bought for d dollars.

Since the units must be consistent, first change d dollars to 100d cents, and then set up a proportion:

Now cross multiply:

TIP

If two variables vary directly, their quotient is a constant.

Rate problems are examples of direct variation. We say that one variable varies directly with a second variable, or that one variable is directly proportional to a second variable, if their quotient is a constant. So if y varies directly with x, there is a constant k such that When two quantities vary directly, as one quantity increases (or decreases), so does the other. The constant is the rate of increase or decrease. In Example 5, the number of words Diane types varies directly with the number of minutes she types. Diane”s rate of typing is 80 words per minute. The quotient is constant:

In contrast to direct variation, in some problems, one variable increases as the other decreases. One example of this is inverse variation. We say that one variable varies inversely with a second variable or one variable is inversely proportional to a second variable, if their product is a constant. So ify varies inversely with x, there is a constant k such that xy = k.

EXAMPLE 7: Boyle”s law states that at a fixed temperature, the volume of a gas varies inversely as the pressure on the gas. If a certain gas occupies a volume of 1.2 liters at a pressure of 20 kilograms per square meter, what volume, in liters, will the gas occupy if the pressure is increased to 30 kilograms per square meter?

Since the volume, V, varies inversely with the pressure, P, there is a constant k such that VP = k. Then

TIP

If two variables vary indirectly, their product is a constant.

EXAMPLE 8: Assume x varies directly with y and inversely with z and that when x is 6, y and z are each 9. What is the value of y + z when x = 9?

Since x varies directly with y, there is a constant k such that Then and when

Since x varies inversely with z, there is a constant c such that xz = c. Then c = (6)(9) = 54. When x = 9, 9z = 54 z = 6.

The value of y + z is 13.5 + 6 = 19.5.

Note: In Example 8, as x increased from 6 to 9, y increased (from 9 to 13.5) and z decreased (from 9 to 6).