SAT SUBJECT TEST MATH LEVEL 1

ALGEBRA

CHAPTER 6
Equations and Inequalities

QUADRATIC EQUATIONS

A quadratic equation is an equation that can be written in the form ax² + bx + c = 0, where a, b, and c are any real numbers with a 0. Any number, x, that satisfies the equation is called a solution or a root of the equation.

Although some quadratic equations can be solved by other, sometimes easier, methods—including factoring—that will be discussed later, every quadratic equation can be solved by using the quadratic formula given in KEY FACT E1.

Key Fact E1

QUADRATIC FORMULA

If a, b, and c are real numbers with a 0 and if ax ² + bx + c = 0, then

Recall that the symbol ± is read “plus or minus” and that is an

abbreviation for or .

As you can see, a quadratic equation has two roots, both of which are determined by the quadratic formula.

The expression b² – 4ac that appears under the square root symbol is called the discriminant of the quadratic equation. As explained in KEY FACT E2, the dis-criminant provides valuable information about the nature of the roots of a quadratic equation. If we let D represent the discriminant, an alternative way to write the quadratic formula is . The following examples illustrate the proper use of the quadratic formula.

EXAMPLE 12: What are the roots of the equation x² – 2x – 15 = 0?

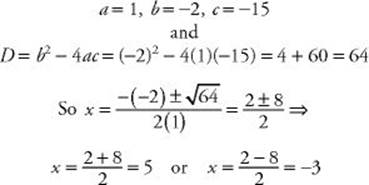
EXAMPLE 13: What are the roots of the equation x² = 10x – 25?

First, rewrite the equation in the form ax² + bx + c = 0:

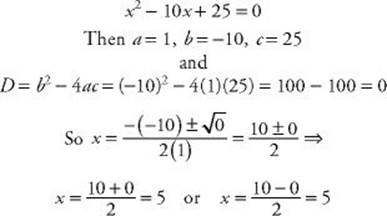
Notice that since 10 + 0 = 10 and 10 – 0 = 10, the two roots are each equal to 5. Although some people would say that the equation x² – 10x + 25 = 0 has only one root, you should say that the equation has two equal roots.

EXAMPLE 14: Solve the equation 2x² – 4x – 1 = 0.

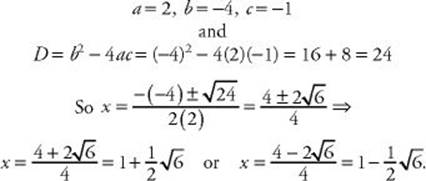
EXAMPLE 15: Solve the equation x² – 2x + 2 = 0.

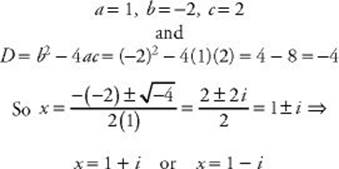
See Chapter 17 for a discussion of the imaginary unit i.

If in the equation ax² + bx + c = 0, either b or c is equal to 0, it is easier not to use the quadratic formula.

Smart Strategy

Before using the quadratic formula, see if another method would be easier and quicker.

• If b = 0, you can just take a square root.

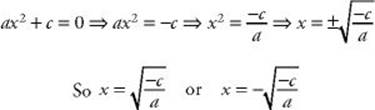
Note that if c 0, the two solutions will be real. If c > 0, the expression under the square root sign will be negative, and the two solutions will be imaginary.

EXAMPLE 16:

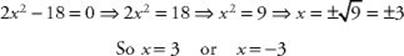
EXAMPLE 17:

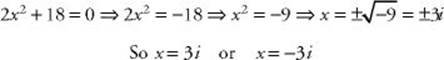
• If c = 0, you should just factor out an x.

Recall that if a product is equal to 0, one of the factors must be 0. So:

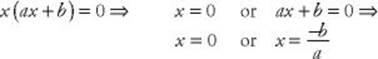
EXAMPLE 18:

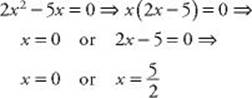
EXAMPLE 19:

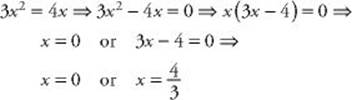
• If you can easily factor the expression ax² + bx + c, then you can solve the equation ax² + bx + c = 0 by setting each factor equal to 0.

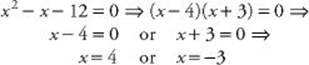
Factoring is faster than using the quadratic formula if you can immediately determine the factors. However, factoring is a trial and error method. Even if an expression factors, it may take you a long time to do so. Worse, after spending a few minutes trying to factor, you may realize that the expression cannot be factored. Now you have to use the quadratic formula, and it would have taken less time to have done so right away.

Consider the equations 2x² + 11x – 24 = 0 and 2x² + 13x – 24 = 0. Only one of them can be solved by factoring. Do you know which one? Probably not. So if you were given one of these equations to solve and you attempted the factoring method, you might waste valuable time in a fruitless effort. Therefore, to solve a quadratic equation, use the quadratic formula unless b = 0 or c = 0 or unless you immediately see how to factor the quadratic expression.

Sometimes a question on a Math 1 test asks for information about the roots of a quadratic equation but does not specifically require you to solve the equation. Looking at the discriminant (D) will allow you to answer such a question.

• If D = 0, as in Example 13, the two roots are and . So the two roots are equal. If a, b, and c are all rational numbers, then is also rational.

• If D is negative, as in Example 15, then the equation has no real roots. Both roots are complex (or imaginary) numbers. (See Chapter 17 for a discussion of complex numbers.) If one of the roots is u + vi, the other root is its conjugate: u – vi.

• If D is positive, as in Examples 12 and 14, then the equation has two unequal real roots. If a, b, and c are rational, then if D is a perfect square, as in Example 12, the two roots are rational; and if D is not a perfect square, as in Example 14, the two roots are irrational.

The preceding remarks are summarized in the following chart.

Key Fact E2

If a, b, and c are rational numbers with a 0, if ax²+ bx + c = 0, and if D = b² – 4ac, then

TIP

Be sure to memorize the facts in this chart.

If ax² + bx + c = 0 and r₁ and r₂ are the two roots, then the sum of the roots is

and the product of the roots is

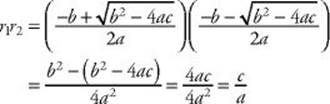
Key Fact E3

If ax² + bx + c = 0, then the sum of the two roots is and the product of the two roots is .

EXAMPLE 20: Find a quadratic equation for which the sum of the roots is 5 and the product of the roots is 5.

For simplicity, let a = 1. Then , and . So the equation x² – 5x + 5 = 0 satisfies the given conditions.