SAT SUBJECT TEST MATH LEVEL 1

ALGEBRA

CHAPTER 7
Word Problems

• Rate Problems

• Age Problems

• Percent Problems

• Integer Problems

• A Few Miscellaneous Problems

• Exercises

• Answers Explained

Every Math 1 test has at least a few word problems. You can encounter word problems on any math topic in the Math 1 syllabus. In this section, you will see a variety of problems involving several areas of mathematics. Read each example carefully, and try to follow the algebraic solution.

To solve word problems algebraically, you must treat algebra as a foreign language and translate “word for word” from English into algebra, just as you would from English into any foreign language. When translating into algebra, you should use some letter (often x) to represent the unknown quantity you are trying to determine. Review all of the examples in this section so that you master this translation process. Once the translation is complete, you will be able to use the techniques presented in Chapter 6 to solve the equation.

TIP

If you get stuck trying to set up or solve a word problem algebraically, use one of the tactics in Chapter 1 to get the correct answer.

RATE PROBLEMS

The basic formula used in all rate problems is

Of course, you can solve for one of the other variables:

Sometimes in rate problems, the word speed is used instead of rate. When you solve word problems, be sure you use consistent units.

EXAMPLE 1: John drove from his house to his office at an average speed of 30 miles per hour. If the trip took 40 minutes, how far, in miles, is it from John”s house to his office?

You know the rate (30 mph) and the time (40 minutes), and you want to find the distance. Of course, you are going to use the formula d = rt. However, if you write d = (30)(40) = 1,200, you know something is wrong. Clearly, John didn”t drive 1,200 miles in less than one hour. The problem is that the units are wrong. The formula is really:

So you have to convert 40 minutes to hours:

Then . So it took John hours to get to his office.

Now you can use the formula d = rt, with r = 30 and .

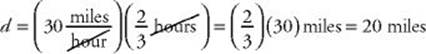
Be sure you understand the explanation in Example 1. It is very important.

The d in the formula d = rt does not have to represent distance ; it could represent any type of work that is performed at a constant rate, r, for a certain time, t. In Example 1, instead of driving 20 miles at 30 miles per hour for 40 minutes, in 40 minutes John could have

• read 20 pages at a rate of 30 pages per hour.

• drawn 20 sketches at a rate of 30 sketches per hour.

• planted 20 flowers at a rate of 30 flowers per hour.

EXAMPLE 2: If Brian can paint a fence in 4 hours and Scott can paint the same fence in 6 hours, when working together, how long will it take the two of them to paint the fence?

Call painting the fence “the job.” Then Brian works at the rate of . Similarly, Scott”s rate of work is . Together they can complete jobs per hour. Finally,

So it will take Brian and Scott hours = 2 hours and 24 minutes to paint the fence.