SAT SUBJECT TEST MATH LEVEL 1

PLANE GEOMETRY

CHAPTER 8 Lines and Angles

Exercises

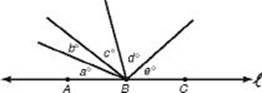
1. In the figure below, A, B, and C are on line . What is the average of a, b, c, d, and e ?

(A) 18

(B) 27

(C) 36

(D) 45

(E) 72

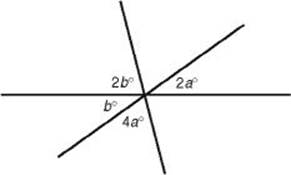
2. In the figure below, what is the value of b ?

(A) 9

(B) 18

(C) 27

(D) 36

(E) 45

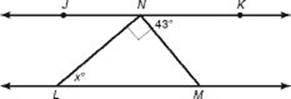
3. In the figure below , is parallel to . What is the value of x?

(A) 37

(B) 43

(C) 47

(D) 53

(E) 57

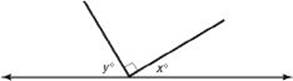
4. In the figure below, what is the value of x if the ratio of y to x is 7 to 3?

(A) 18

(B) 27

(C) 30

(D) 36

(E) 63

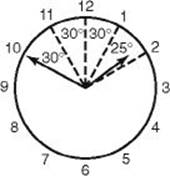
5. What is the measure of the angle formed by the minute and hour hands of a clock at 1:50?

(A) 90°

(B) 95°

(C) 105°

(D) 115°

(E) 120°

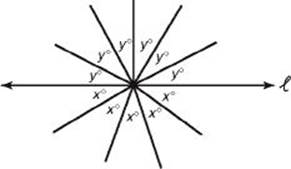
6. In the figure below, what is the value of ?

(A) 6

(B) 11

(C) 22

(D) 30

(E) 36

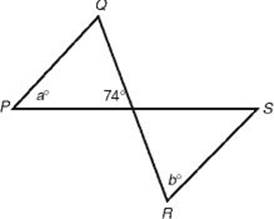
7. In the figure below, is parallel to . What is the value of a + b ?

(A) 47

(B) 74

(C) 90

(D) 106

(E) It cannot be determined from the information given

8. In the figure below, a : b = 3 : 5 and c : b = 2 : 1. What is the measure of the largest angle?

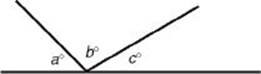
Note: Figure not drawn to scale.

(A) 50°

(B) 90°

(C) 100°

(D) 120°

(E) 150°

9. A, B, and C are points on a line with B between A and C. Let M and N be the midpoints of and , respectively. If AB : BC = 3 : 1, what is MN : BC?

(A)

(B)

(C)

(D)

(E)

10. In the figure below, what is the average (arithmetic mean) of the measures of the five angles?

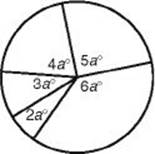
(A) 18°

(B) 36°

(C) 45°

(D) 72°

(E) It cannot be determined from the given information

ANSWERS EXPLAINED

Answer Key

Solutions

Each of the problems in this set of exercises is typical of a question you could see on a Math 1 test. When you take the model tests in this book and, in particular, when you take the actual Math 1 test, if you get stuck on questions such as these, you do not have to leave them out—you can almost always answer them by using one or more of the strategies discussed in the “Tactics” chapter. The solutions given here do not depend on those strategies; they are the correct mathematical ones.

See Important Tactics for an explanation of the symbol ⇒, which is used in several answer explanations.

1. (C) Since is a straight angle, by KEY FACT G2, the sum of a, b, c, d, and e is 180, and so their average is .

2. (D) Since vertical angles are congruent, the two unmarked angles are 2b and 4a. Since the sum of all six angles is 360°:

360 = 4a + 2b + 2a + 4a + 2b + b = 10a + 5b

Since vertical angles are congruent, b = 2a 5b = 10a. Hence:

360 = 10a + 5b = 10a + 10a = 20a a = 18 b = 36

3. (C) Let y be the degree measure of . Then by KEY FACT G2:

43 + 90 + y = 180 133 + y = 180 y = 47

Since is parallel to , by KEY FACT G6, x = y x = 47.

4. (B) x + y + 90 = 180 x + y = 90

Since the ratio of y to x is 7 to 3, y = 7t and x = 3t. So:

7t + 3t = 90 10t = 90 t = 9 x = 3(9) = 27

5. (D) For problems such as this, always draw a picture. The measure of each of the 12 central angles from one number to the next is 30°. At 1:50, the minute hand is pointing at the 10, and the hour hand has gone of the way from the 1 to the 2. From the 10 to the 1 is 90° and from the 1 to the hour hand is , for a total of 90° + 25° = 115°.

6. (B) From the diagram, we see that 6y = 180, which implies that y = 30 and that 5x = 180, which implies that x = 36. So:

7. (D) Since is parallel to and so b = m∠Q

m

8. (C) Since a : b = 3 : 5, a = 3x and b = 5x. Since c : b = 2 : 1, c = 2b = 10x. Then:

3x + 5x + 10x = 180 18x = 180 x = 10 c = 10x = 100

9. (D) If a diagram is not provided on a geometry question, draw one. From the figure below, you can see that MN : BC = 2 : 1.

10. (D) The markings in the five angles are irrelevant. The sum of the measures of the five angles is 360°, and 360° 5 = 72°.