SAT SUBJECT TEST MATH LEVEL 1

PLANE GEOMETRY

CHAPTER 9 Triangles

SPECIAL RIGHT TRIANGLES

Let x be the length of each leg and let h be the length of the hypotenuse of an isosceles right triangle. By the Pythagorean theorem,

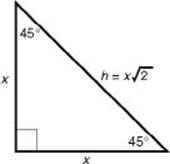
Key Fact H7

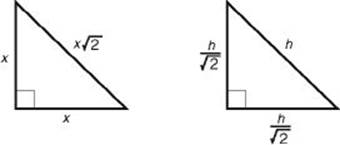
In a 45-45-90 right triangle, the sides are x, x, and x .

• If you are given the length of a leg, multiply it by to get the length of the hypotenuse.

• If you are given the length of the hypotenuse, divide it by to get the length of each leg.

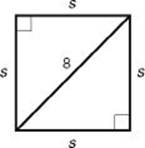
EXAMPLE 5: To find the area of a square whose diagonal is 8, note that the diagonal divides the square into two isosceles right triangles. So .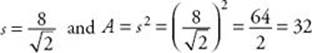

Let 2x be the length of each side of equilateral PQR, in which altitude has been drawn. Then PQS is a 30-60-90 right triangle, and its sides are x, 2x, and h. By the Pythagorean theorem,

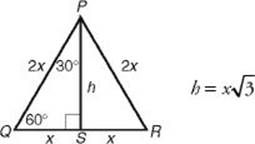
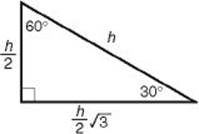
Key Fact H8

In a 30-60-90 right triangle, the sides are x, x , and 2x.
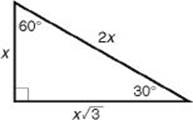
If you know the length of the shorter leg (x):

• Multiply it by to get the length of the longer leg.

• Multiply it by 2 to get the length of the hypotenuse.

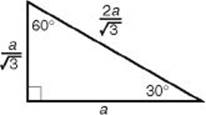
If you know the length of the longer leg (a):

• Divide it by to get the length of the shorter leg.

• Multiply the length of the shorter leg by 2 to get the length of the hypotenuse.

If you know the length of the hypotenuse (h):

• Divide it by 2 to get the length of the shorter leg.

• Multiply the length of the shorter leg by to get the length of the longer leg.