SAT SUBJECT TEST MATH LEVEL 1
PLANE GEOMETRY
![]()
CHAPTER 9 Triangles
![]()
SIMILAR TRIANGLES
Two triangles, such as triangle I and triangle II in the figure below, that have the same shape but not necessarily the same size are said to be similar.
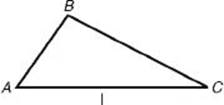
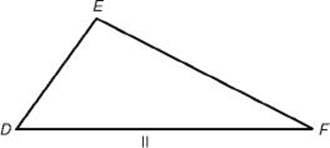
The following KEY FACT makes this intuitive definition mathematically precise.
Key Fact H12
Two triangles are similar provided the following two conditions are satisfied:
• The three angles in the first triangle have the same measures as the three angles in the second triangle.
m∠A = m∠D m∠B = m∠E m∠C = m∠F
• The lengths of the corresponding sides of the two triangles are in proportion.
![]()
Remember
Corresponding sides are sides that are opposite angles of the same measure.
An important theorem in geometry states that if the first condition in KEY FACT H12 is satisfied, then the second condition is automatically satisfied. Therefore, to show that two triangles are similar, it is sufficient to show that their angles have the same measures. Furthermore, if the measures of two angles of one triangle are equal to the measures of two angles of a second triangle, then the measures of the third angles are also equal. KEY FACT H13 is an immediate consequence of the results in this paragraph.
Key Fact H13
If the measures of two angles of one triangle are equal to the measures of two angles of a second triangle, then the triangles are similar.
EXAMPLE 9: Find the length of ![]() in the diagram below.
in the diagram below.
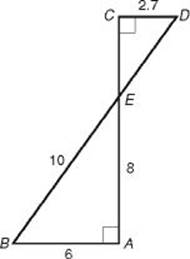
First note that since vertical angles have equal measures, m∠AEB = m∠DEC and, of course, m∠A = m∠C. So the measures of two angles of ![]() ABE are equal to the measures of two angles of
ABE are equal to the measures of two angles of ![]() CDE. By KEY FACT H13, the two triangles are similar. So, by KEY FACT H12, corresponding sides of the triangles are in proportion. Therefore:
CDE. By KEY FACT H13, the two triangles are similar. So, by KEY FACT H12, corresponding sides of the triangles are in proportion. Therefore:
![]()
6(ED) = 27, and so cross-multiplying, we get ![]()
In ![]() ABC below, line
ABC below, line ![]() is parallel to side
is parallel to side ![]() and intersects sides
and intersects sides ![]() and
and ![]() at D and E, respectively. Then by KEY FACT G6, m∠AED = m∠C and m∠ADE = m∠B. So by KEY FACT H13,
at D and E, respectively. Then by KEY FACT G6, m∠AED = m∠C and m∠ADE = m∠B. So by KEY FACT H13, ![]() AED is similar to
AED is similar to ![]() ACB.
ACB.
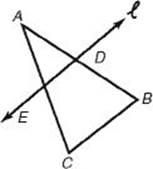
Key Fact H14
A line that intersects two sides of a triangle and is parallel to the third side creates a smaller triangle that is similar to the original one.
If two triangles are similar, the common ratio of their corresponding sides is called the ratio of similitude.
Key Fact H15
If two triangles are similar, and if k is the ratio of similitude:
• The ratio of all their linear measurements is k.
• The ratio of their areas is k2.
In the figure below, ![]() . By KEY FACT H14,
. By KEY FACT H14, ![]() ABC and
ABC and ![]() DBE are similar.
DBE are similar.
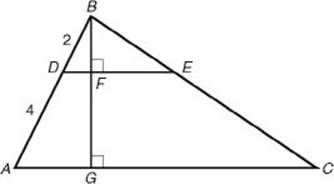
Then ![]() and
and ![]() are corresponding sides. Since AB = 6 and DB = 2, the ratio of similitude is
are corresponding sides. Since AB = 6 and DB = 2, the ratio of similitude is ![]() .
.
Therefore:
• All the sides are in the ratio of ![]() : BC = 3 × BE and AC = 3 × DE
: BC = 3 × BE and AC = 3 × DE
• The altitudes are in the ratio of ![]() : BG = 3 × BF
: BG = 3 × BF
• The perimeters are in the ratio of : ![]()
perimeter of ![]() ABC = 3
ABC = 3 ![]() (perimeter of
(perimeter of ![]() DBE )
DBE )
• The areas are in the ratio of ![]() : area of
: area of ![]() ABC = 9
ABC = 9 ![]() (area of
(area of ![]() DBE )
DBE )