SAT SUBJECT TEST MATH LEVEL 1

PLANE GEOMETRY

CHAPTER 10
Quadrilaterals and Other Polygons

PERIMETER AND AREA OF QUADRILATERALS

The perimeter (P ) of a polygon is the sum of the lengths of all of its sides. The area (A) of a polygon is the amount of space it encloses (measured in square units). The perimeter and area formulas you need to know for the Math 1 test are given in KEY FACTS I8 and I9.

Key Fact I8

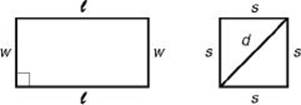
PERIMETERS

• For a rectangle: P = 2( + w)

• For a square: P = 4s

Key Fact I9

AREAS

• For a parallelogram: A = bh

• For a rectangle: A = w

• For a square: A = s² or

• For a trapezoid:

TIP

Here”s a useful alternate formula for the area of a square:
If d is the diagonal of a square, then the area of the square is .

EXAMPLE 3: What are the perimeter and area of a rhombus whose diagonals are 6 and 8? First draw and label a rhombus.

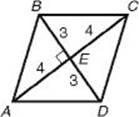
Since the diagonals bisect each other, BE = ED = 3 and AE = EC = 4. Also, since the diagonals of a rhombus are perpendicular, ∠BEA is a right angle and BEA is a 3-4-5 right triangle. So AB = 5 and the perimeter of the rhombus is 4 5 = 20. The easiest way to calculate the area of the rhombus is to recognize that it is the sum of the areas of four 3-4-5 right triangles. Since each triangle has an area of , the area of the rhombus is 4 6 = 24.

EXAMPLE 4: In the figure below, the area of parallelogram ABCD is 40. What are the areas of rectangle AFCE, trapezoid AFCD, and triangle BCF ?

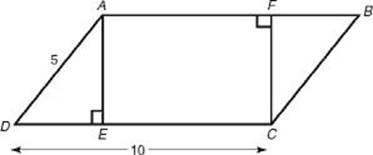
Since the base of parallelogram ABCD is 10 and its area is 40, its height, AE, must be 4. Then ΔAED must be a 3-4-5 right triangle with DE = 3, which implies that EC = 7. So the area of rectangle AFCE is 7 4 = 28; the area of trapezoid AFCD is ; and the area of each small triangle is .