TANGENTS TO A CIRCLE - Circles - PLANE GEOMETRY - SAT SUBJECT TEST MATH LEVEL 1

SAT SUBJECT TEST MATH LEVEL 1

PLANE GEOMETRY

CHAPTER 11
Circles

TANGENTS TO A CIRCLE

A line or line segment is tangent to a circle if it intersects the circle exactly once.

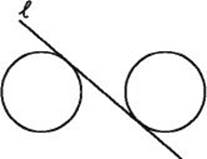
Line is tangent to both circles.

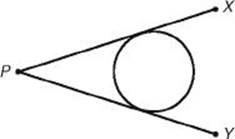
and are each tangent to the circle.

The following KEY FACT lists four important theorems about tangents.

Key Fact J11

• From any point outside a circle, exactly two tangents can be drawn to the circle.

• If two tangents are drawn from a point P outside a circle, intersecting the circle at A and B, then PA = PB.

• The measure of the angle formed by two tangents drawn from the same point is one-half the difference of the two intercepted arcs.

• A line tangent to a circle is perpendicular to the radius (or diameter) drawn to the point of contact.

EXAMPLE 5: In the diagram below and are tangent to circle O. What is m∠P?

By the fourth theorem in KEY FACT J11, m∠PAO = m∠PBO = 90°. Since the sum of the measures of the four angles in quadrilateral PAOB is 360°:

90° + 140° + 90° + m∠P = 360° ⇒ m∠P = 40°

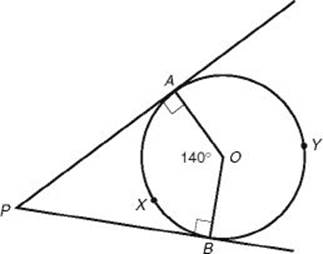
Another way to evaluate m P is to observe that since AOB is a central angle, the measure of arc is 140° and the measure of arc is 360° – 140° = 220°. Then, by the third theorem in KEY FACT J11:

m

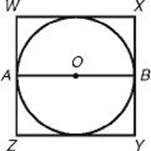
Key Fact J12

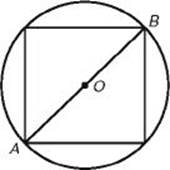
• When a square is inscribed in a circle, the diagonals of the square are diameters of the circle. ( is a diagonal and a diameter.)

• When a circle is inscribed in a square, the length of a diameter is equal to the length of a side of the square. (AB = WX )

EXAMPLE 6: In the diagram below, the circle is inscribed in square ABCD, and square PQRS is inscribed in the circle.

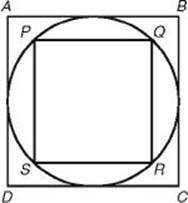
What is the ratio of the area of the large square to the area of the small square?

Choose any number for the sides of square PQRS, say PQ = 2.

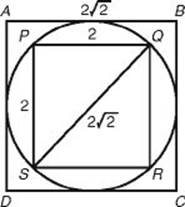
Then the area of square PQRS is 4. Since ΔPQS is an isosceles right triangle, QS = 2. Since diagonal is a diameter of the circle, by the second statement in KEY FACT J12, 2 = is also the length of side of square ABCD. So the area of square ABCD is (2)2 = 8 . Finally, the ratio of the area of square ABCD to the area of square PQRS is 8 : 4 or 2 : 1.