SAT SUBJECT TEST MATH LEVEL 1
SOLID AND COORDINATE GEOMETRY
![]()
CHAPTER 12 Solid Geometry
![]()
CONES
Imagine taking a cylinder and shrinking the size of one of the circular bases.
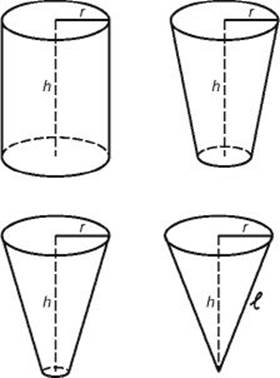
When it shrinks to a point, we call the resulting solid a cone. If you picture an ice cream cone (without the ice cream) or a dunce cap, you have the right idea. Notice that the radius of the circular base and the height of the cone are the same as in the original cylinder. In the figure above, ![]() is called the slant height of the cone.
is called the slant height of the cone.
In the Math 1 “Reference Information,” cones are referred to as “right circular cones.” This is done to emphasize that the base is a circle and that the height (the line segment joining the vertex and the center of the circular base) is perpendicular to the base. KEY FACT K6 lists the two formulas concerning cones that are given to you in the “Reference Information” box on the first page of the test and gives an alternative for one of them. Note that in the second formula, the circumference of the circular base is denoted by a lowercase “c,” whereas we usually use an uppercase “C” to represent circumference. Also, ![]() , the slant height, is the distance from any point on the circumference to the vertex of the cone.
, the slant height, is the distance from any point on the circumference to the vertex of the cone.
Key Fact K6
• The formula for the volume of a right circular cone is ![]() .
.
• The formula for the lateral surface area of a right circular cone is ![]() ,where c is the circumference and
,where c is the circumference and ![]() is the slant height.
is the slant height.
• Since ![]() , so an alternative formula for the lateral surface area is A = πr
, so an alternative formula for the lateral surface area is A = πr![]() .
.
• The total surface area of a cone is the sum of its lateral area and the area of its circular base: SA = πr![]() + πr 2.
+ πr 2.
Remember
The first two formulas in KEY FACT K6 are listed in the Reference Information box on the first page of every Math 1 test.
EXAMPLE 5: Assume that the volumes of a right circular cone and a right circular cylinder are equal and that the radius of the cone is twice the radius of the cylinder. How do their heights compare?
Let r be the radius of the cylinder, 2r the radius of the cone, and h and H the heights of the cone and the cylinder, respectively. Then
![]()