DISTANCE BETWEEN TWO POINTS - Coordinate Geometry - SOLID AND COORDINATE GEOMETRY - SAT SUBJECT TEST MATH LEVEL 1

SAT SUBJECT TEST MATH LEVEL 1

SOLID AND COORDINATE GEOMETRY

CHAPTER 13
Coordinate Geometry

• Distance Between Two Points

• The Midpoint of a Segment

• Slope

• Equations of Lines

• Circles and Parabolas

• Exercises

• Answers Explained

Of the 50 questions on the Math 1 test, approximately six are on the coordinate geometry topics specifically discussed in this chapter. In addition, three or four more questions that the College Board would classify under other topics, such as functions and their graphs or even probability or trigonometry, could be considered as coordinate geometry questions. So this is an important topic that you should review thoroughly.

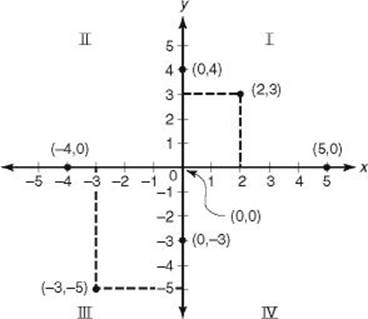
The coordinate plane is formed by two perpendicular number lines called the x-axis and y-axis, which intersect at the origin. The axes divide the plane into four quadrants, labeled I, II, III, and IV as shown in the figure below. Each point in the plane is assigned two numbers, an x-coordinateand a y-coordinate, which are written as an ordered pair, (x, y). The point (2, 3) has an x-coordinate of 2 and a y-coordinate of 3 and is located at the intersection of the vertical line that crosses the x-axis at 2 and the horizontal line that crosses the y-axis at 3.

Key Fact L1

• The y-coordinate of every point on the x-axis is 0.

• The x-coordinate of every point on the y-axis is 0.

• To find the x-intercepts of a graph, replace y by 0 in the equation of the graph.

• To find the y-intercepts of a graph, replace x by 0 in the equation of the graph.

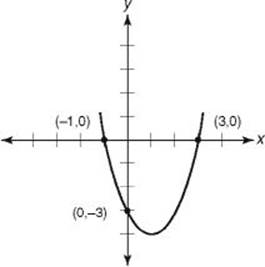
EXAMPLE 1: Where does the graph of y = x 2 – 2x – 3 cross the x-axis and where does it cross the y-axis?

By KEY FACT L1, the x-intercepts are the points whose y-coordinates are 0. So replace y with 0:

The x-intercepts of this graph are the points (–1, 0) and (3, 0).

By KEY FACT L1, the y-intercept is the point whose x-coordinate is 0. So replace x with 0:

The y-intercept is the point (0, –3).

The graph of y = x 2 – 2x – 3 is the parabola in the figure below, on which the x- and y-intercepts are indicated.

DISTANCE BETWEEN TWO POINTS

Often a question on the Math 1 test requires you to find the distance between two points. This is easiest when the points lie on the same horizontal or vertical line.

Key Fact L2

• All the points on a horizontal line have the same y-coordinate. To find the distance between them, subtract their x-coordinates.

• All the points on a vertical line have the same x-coordinate. To find the distance between them, subtract their y-coordinates.

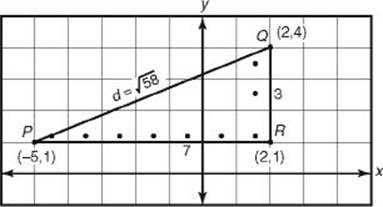
In the diagram above, the distance from P to R is 2 − (−5) = 7 and the distance from R to Q is 4 − 1 = 3. If you want to find the distance between two points, such as P and Q, that do not lie on the same horizontal or vertical line, sketch the line segment joining those points and then create a right triangle with that segment as the hypotenuse by drawing a horizontal line through one of the points and a vertical line through the other. Use KEY FACT L2 to find the length of the legs. To calculate the hypotenuse, use the Pythagorean theorem. For example, in the figure above, if d represents the distance from P to Q,

An alternative method is to use the distance formula given in KEY FACT L3.

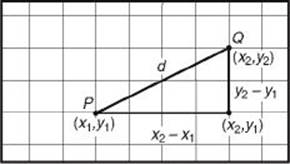
Key Fact L3

The distance, d, between two points, P1(x1, y1) and P2(x2, y2), can be calculated using the distance formula:

From the diagram below, you should see that the distance formula is really just the Pythagorean theorem.

EXAMPLE 2: If A (–2, 5), B (–2, –3), and C (2, 2) are the vertices of ABC, what are the area and perimeter of the triangle?

Start by making a sketch, and then calculate the lengths of the three line segments.

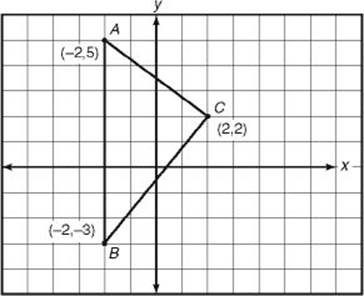
Since A and B lie on the same vertical line, we can find AB by subtracting their y-coordinates: AB = 5 – (–3) = 8.

Now draw in altitude .

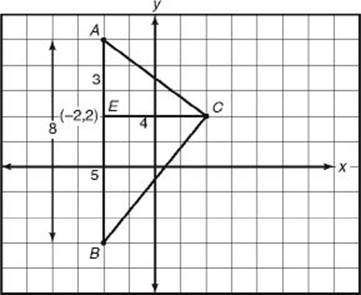
Since is horizontal, CE = 2 – (–2) = 4. If we treat as the base of ABC, then is the height, and the area of the triangle is (8)(4)=16 .

On Example 2, we found that AB = 8. To find the perimeter of ABC, we need the lengths of the other two sides. Each of these can be calculated using the distance formula or the Pythagorean theorem:

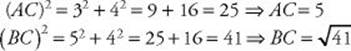
So the perimeter of ABC is