SAT SUBJECT TEST MATH LEVEL 1

FUNCTIONS

CHAPTER 15
Functions and Graphs

INVERSE FUNCTIONS

If f and g are functions such that

(1) for every x in the domain of g, f (g (x)) = x and

(2) for every x in the domain of f, g (f (x)) = x,

then we say that g is the inverse of f and write g = f ^–1, which is read “f inverse.” It is also true that f is the inverse of g: f = g^–1.

Key Fact N7

If for some function f, f ^–1 exists, then

f (f ^–1(x)) = x and f ^–1(f (x)) = x.

The inverse, f ^–1, of a function, f, undoes what f does. In Example 15, f multiplies a number by 3 and then subtracts 2 from it; g, which is f ^–1, adds 2 to a number and then divides the result by 3.

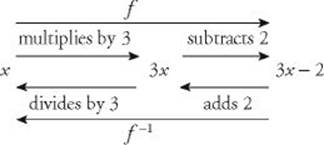
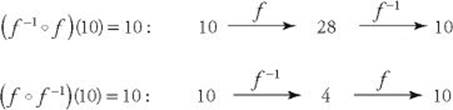
Not every function has an inverse, but many do. On the Math 1 test, you may be asked to find the inverse of a particular function. The procedure to do this is given in KEY FACT N8.

Key Fact N8

If f is a function of x, to find f ^–1, first write y = f (x). Then interchange x and y and solve for y.

EXAMPLE 16: If f (x) = 3x – 2, what is f ^–1(x)?

Write y = 3x – 2. Then switch the x and y: x = 3y – 2. Now solve for y :

So f ^–1x = . Note that f ^–1, which is function g in Example 15, simply undoes what f does: f multiplies a number by 3 and then subtracts 2; f ^–1 adds 2 to a number and then divides the result by 3.