SAT SUBJECT TEST MATH LEVEL 1

MISCELLANEOUS TOPICS

CHAPTER 18
Sequences

ARITHMETIC SEQUENCES

An arithmetic sequence is a sequence such as 5, 8, 11, 14, 17, . . . in which the difference between any two consecutive terms is the same. In this sequence, the difference is 3 (8 – 5 = 3; 11 – 8 = 3; 14 – 11 = 3, . . .). An easy way to find the nth term of such a sequence is to start with the first term and add the common difference n – 1 times. Here, the 5th term is 17 which can be obtained by taking the first term, 5, and adding the common difference, 3, four times: 5 + 4(3) = 17. In the same way, the 100th term is 5 + 99(3) = 5 + 297 = 302.

Key Fact Q2

If a₁, a₂, a₃, . . . is an arithmetic sequence whose common difference is d, then a_n = a₁+ (n – 1)d.

EXAMPLE 4: If the 8th term of an arithmetic sequence is 10 and the 20th term is 58, what is the first term?

Use KEY FACT Q2 twice and subtract:

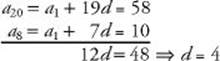
Then

10 = a₁ + 7d = a₁ + 7(4) = a₁ + 28 a₁ = –18