Model Test 1 - MODEL TESTS - SAT SUBJECT TEST MATH LEVEL 1

SAT SUBJECT TEST MATH LEVEL 1

MODEL TESTS

Guidelines and Scoring

The three model tests in this section have the identical format as the actual Math 1 test you will take. There are 50 multiple-choice questions that generally proceed from easy to medium to difficult. On each test the percentage of questions on each topic in the Math 1 syllabus follows the breakdown in the chart on WHAT TOPICS ARE COVERED?.

To simulate as closely as possible the experience of taking a Math 1 test, you should follow these guidelines:

• Take the test in a quiet room in which there are no distractions. In particular, you should not be listening to music and your cell phone should be turned off.

• Give yourself exactly 60 minutes to complete the test. When you take the model tests, as well as when you take your actual Math 1 test, you should have an easy-to-read clock, stopwatch, or wrist watch on your desk.

• When you take the model tests, use the same calculator that you intend to use on the actual Math 1 test.

• Tear out the answer sheet and use it to bubble in your answers as you take each test.

• If necessary, before starting the test read over the directions that are printed on the first page. Familiarize yourself with them. On the day you take the actual Math 1 test, do not spend even one second reading the directions.

• You don’t have to memorize the five formulas that are given to you in the reference box, but be sure that you know which formulas are there. If there are any formulas other than the five in the box that you want to review, do so now.

After you complete each model test:

• Use the Answer Key to calculate your raw score: give yourself 1 point for each correct answer and deduct point for each incorrect answer.

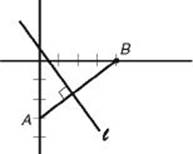
• Then use the conversion chart to find your scaled score.

• Carefully read the solutions to each question that you left out or missed.

• If there is still anything you do not understand, look up those topics in the math review chapters and do the exercises at the end of each section covering a topic for which you needed extra help.

• Please Note: All directions in the Model Tests are similar to those on the actual exam. Please record all answers separately for this e-Book. Answer sheets are for reference only.

CHAPTER 20 Model Test 1

50 Questions / 60 MINUTES

Directions: For each question, determine which of the answer choices is correct and fill in the oval on the answer sheet that corresponds to your choice.

Notes :

1. You will need to use a scientific or graphing calculator to answer some of the questions.

2. Be sure your calculator is in degree mode.

3. Each figure on this test is drawn as accurately as possible unless it is specifically indicated that the figure has not been drawn to scale.

4. The domain of any function f is the set of all real numbers x for which f (x) is also a real number, unless the question indicates that the domain has been restricted in some way.

5. The box below contains five formulas that you may need to answer one or more of the questions.

Reference Information. This box contains formulas for the volumes of three solids and the areas of two of them.

For a sphere with radius r :

•

• A = 4πr2

For a right circular cone with radius r, circumference c, height h, and slant height l:

•

•

For a pyramid with base area B and height h:

•

1. If then x =

(A) –3

(B) 1.5

(C) 3

(D) 7.5

(E) 21

2. If a = b2, b = c, and a = 18, which of the following could be the value of c ?

(A) 3

(B) 3

(C) 9

(D) 81

(E) 162

3. What is the value of

(A) –12

(B) –2

(C) 2

(D) 12

(E) 35

Note: Figure not drawn to scale.

4. In the figure above, what is the value of a ?

(A) 70

(B) 100

(C) 110

(D) 120

(E) 290

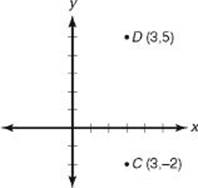
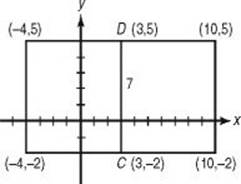
5. In the diagram above, C (3, –2) and D (3, 5) are two adjacent vertices of square ABCD. Which of the following could be the coordinates of A or B?

(A) (–3, –2)

(B) (–2, 3)

(C) (–4, 5)

(D) (3, 10)

(E) (10, 3)

6. For all x –5, 3, which of the following is equivalent to

(A) x2 – 2

(B) x2 – 4

(C)

(D)

(E)

7. One week Susan earned $1,000, which consisted of a base salary of $475 and a 7% commission on her sales. What was the amount of her sales for that week?

(A) $36.75

(B) $75.25

(C) $700

(D) $6,786

(E) $7,500

8. If the sum of two numbers is 5 and the difference of the two numbers is 5, what is the product of the two numbers?

(A) 0

(B) 1

(C) 5

(D) 10

(E) 25

9. If f (x) = –2x2 – 3x, f (–5) =

(A) –65

(B) –35

(C) 35

(D) 85

(E) 115

10. The circumference of circle O is a inches, and the area of circle O is b square inches. If a = b, what is the radius of circle O?

(A) 1

(B) 2

(C) 4

(D) 2π

(E) 4π

11. For what values of n is

(A) only

(B) only

(C) only

(D) and –

(E) and

12. For how many integer values of x can 6, 8, and x be the lengths of the three sides of a triangle?

(A) 1

(B) 2

(C) 10

(D) 11

(E) 13

13. If a = the number of even primes,
 b = the number of primes divisible by 7,
 c = the number of primes divisible by 9, and
 d = the number of primes between 20 and 30,
what is the value of a + b + c + d?

(A) 2

(B) 3

(C) 4

(D) 5

(E) 6

14. If f (x) = x2 – 11, for what values of x is f (x) < 25?

(A) x < 5

(B) x < 6

(C) x = 6

(D) –5 < x < 5

(E) –6 < x < 6

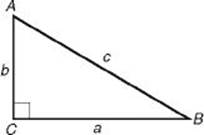
15. In ABC in the figure above, which of the following is equal to a?

I.

II. c sin A

III. b tan A

(A) I only

(B) II only

(C) III only

(D) I and II only

(E) I, II, and III

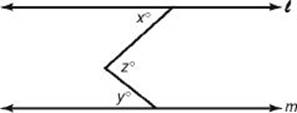
16. If in the figure above, || m, which of the following is a correct relationship between x, y, and z ?

(A) y = x

(B) y = x – z

(C) x = z – y

(D) x + y + z = 180

(E) There is not enough information to determine a relationship.

17. If a and b are positive integers and ab is divisible by 6, which of the following must be true?

I. a or b is divisible by 2 and the other is divisible by 3.

II. a or b is divisible by 6.

III. ab is divisible by both 2 and 3.

(A) None

(B) I only

(C) II only

(D) III only

(E) I and III only

18. What is the slope of the perpendicular bisector of line segment if A = (0, –3) and B = (4, 0)?

(A)

(B)

(C) 0

(D)

(E)

19. If 23x–1 = 16, then x =

(A) 0

(B)

(C)

(D) 1

(E)

20. If the length and width of a rectangular solid are increased by 20% and the height is increased by 25%, by what percent is the volume of the solid increased?

(A) 1%

(B) 21.67%

(C) 65%

(D) 80%

(E) 180%

21. Which of the following is the equation of a parabola that passes through the points (0, 3) and (3, 0)?

(A) y = –x + 3

(B) x2 + y2 = 9

(C) y = x2 + 3

(D) y = –x2 + 2x + 3

(E) y = x3 – 3x2 – x + 3

22. If a 3-digit number is chosen at random, what is the probability that all three digits are prime numbers?

(A)

(B)

(C)

(D)

(E)

23. If the lines whose equations are y = ax + b and x = cy + d are parallel, which statement must be true?

(A)

(B)

(C) c = a

(D) c = –a

(E) a + c = –1

24. The domain of each of the following includes –5 EXCEPT

(A)

(B)

(C)

(D)

(E)

25. If in right ABC, sin , then what is the value of sin B ?

(A)

(B)

(C)

(D)

(E)

5 | 8 9

6 | 0 4 6 8

7 | 3 5 5 5 6 7 7 9

8 | 2 2 3 5

9 | 0 1 4 4 4 8 9

Legend: 8 | 2 represents a grade of 82

26. The stem-and-leaf plot above gives the grades of the students in Mr. Smith’s second period math class on the final exam. What percent of the students earned grades greater than 75?

(A) 15%

(B) 40%

(C) 50%

(D) 60%

(E) 75%

27. How many integers satisfy the inequality

(A) 5

(B) 11

(C) 14

(D) 15

(E) Infinitely many

28. In 2004, Hamburger Heaven sold 20% more cheeseburgers than in 2003, and in 2004 the price of each cheeseburger they sold was 10% more than in 2003. The total income from the sale of cheeseburgers was what percent greater in 2004 than in 2003?

(A) 2%

(B) 20%

(C) 22%

(D) 30%

(E) 32%

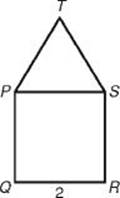
29. In the figure above, PQRS is a square and PST is an equilateral triangle. If QR = 2, what is the length of QT (not shown)?

(A) 3.48

(B) 3.62

(C) 3.86

(D) 3.91

(E) 4.12

30. What is the greatest integer k for which the equation x2 + 5x + k = 0 has real solutions?

(A) 4

(B) 6

(C) 7

(D) 12

(E) 16

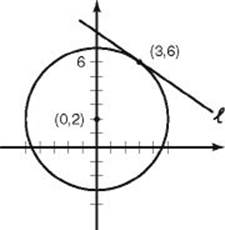
31. What is the equation of the line that is tangent to the circle whose center is at (0, 2) and whose radius is 5 at the point (3, 6)?

(A) y = 3x + 6

(B)

(C)

(D)

(E)

32. In how many ways can Al, Bob, Carol, Diane, and Ed stand in a straight line if Bob must be in the middle and Ed must be at one end?

(A) 6

(B) 12

(C) 24

(D) 48

(E) 120

33. For which of the following quadratic equations is the sum of its roots equal to the product of its roots?

(A) x2 + 5x + 5 = 0

(B) x2 – 5x + 5 = 0

(C) 2x2 – 3x + 6 = 0

(D) 2x2 + 3x – 6 = 0

(E) 2x2 – 6x + 3 = 0

34. If Adam can mow a large yard in 3 hours and Matthew can mow the same yard in 5 hours, when working together, how long will it take, in minutes, for the two boys to mow the yard?

(A) 92

(B) 112.5

(C) 120

(D) 132.5

(E) 240

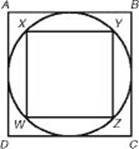
35. In the diagram above, a circle is inscribed in square ABCD and square WXYZ is inscribed in the circle. What is the ratio of the perimeter of square ABCD to the perimeter of square WXYZ?

(A) 2

(B) 2

(C)

(D)

(E)

36. If f (x) = |x + 1| and g (x) = x2 – 5, which of the following is the graph of y = f (g (x))?

(A)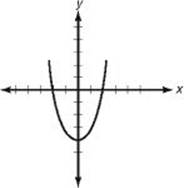

(B)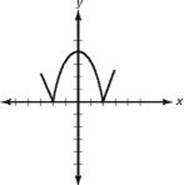

(C)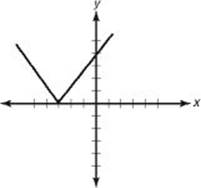

(D)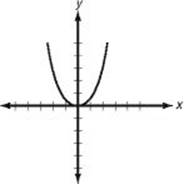

(E)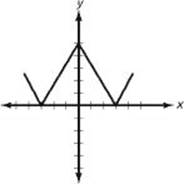

37. Which of the following is equivalent to (sin + cos )2 + (sin – cos )2?

(A) 0

(B) 2

(C) 2sin2

(D) 2sin cos

(E) 4sin cos

38. If i2 = –1, what is the value of i75 – (–i )75?

(A) –2i

(B) 2i

(C) –2

(D) 0

(E) 2

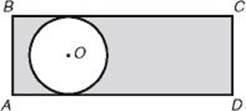
39. In the figure above, circle O is tangent to sides and of rectangle ABCD. If the area of the shaded region is 3 times the area of the circle, what is the ratio of the length of side to the circumference of the circle?

(A)

(B) 1

(C)

(D) 3

(E) π

40. Which of the following is the x-coordinate of a point where the circle whose center is (3, –4) and whose radius is 7 intersects the x-axis?

I. –2.74

II. 0

III. 2.74

(A) None

(B) I only

(C) II only

(D) III only

(E) I and II only

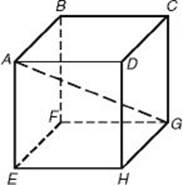
41. In cube ABCDEFGH, the length of diagonal is 9. What is the total surface area of the cube?

(A) 27

(B) 81

(C) 162

(D) 9

(E) 81

42. If which of the following is a number that is NOT in the range of f ?

(A) 1

(B) 0.5

(C) 0

(D) –0.5

(E) –1

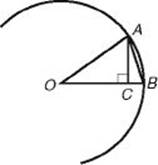
43. The figure above shows an arc of a circle whose center is at O. If OA = 2 and AC = 1, what is the area of ACB ?

(A)

(B) 2 –

(C) 1

(D) 2

(E)

44. If what is the value of f –1(7)?

(A) –7

(B) 7

(C) 42

(D) 189

(E) 2,737

45. At a national educational conference, all of the participants are teachers or administrators. If there are 584 teachers at the conference and 27% of the participants are administrators, how many administrators are attending the conference?

(A) 158

(B) 216

(C) 312

(D) 800

(E) 2,163

46. What is the area of rhombus ABCD, if AB = 10 and m

(A) 50

(B) 64.6

(C) 70.7

(D) 78.2

(E) 100

47. If the statement “All practical numbers are prime” is false, which of the following statements must be true?

(A) No practical numbers are prime.

(B) No prime numbers are practical.

(C) Some practical numbers are prime.

(D) Some practical numbers are not prime.

(E) Some prime numbers are not practical.

48. The base of pyramid 1 is a 3-4-5 triangle, and the base of pyramid 2 is a square whose sides are 3. If the volumes of the pyramid are equal, what is the ratio of the height of pyramid 1 to the height of pyramid 2?

(A)

(B)

(C)

(D)

(E)

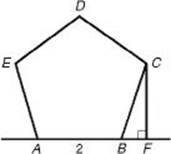
49. In the figure above, ABCDE is a regular pentagon, B lies on and . If AB = 2, what is the area of BFC ?

(A) 0.59

(B) 1.00

(C) 1.18

(D) 1.90

(E) 2.00

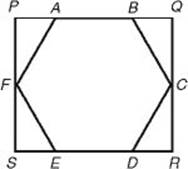
50. In the figure above, regular hexagon ABCDEF is inscribed in rectangle PQRS. If each side of the hexagon is 1, what is the area of the rectangle?

(A) 2

(B) 4

(C) 6

(D)

(E) 2

Answer Key
MODEL TEST 1

1. D

18. A

35. C

2. A

19. E

36. B

3. C

20. D

37. B

4. C

21. D

38. A

5. C

22. D

39. B

6. C

23. B

40. B

7. E

24. B

41. C

8. A

25. C

42. A

9. B

26. D

43. A

10. B

27. D

44. E

11. A

28. E

45. B

12. D

29. C

46. C

13. C

30. B

47. D

14. E

31. E

48. D

15. E

32. B

49. A

16. C

33. B

50. E

17. D

34. B

ANSWERS EXPLAINED

For many of the questions in this model test, an alternative solution, indicated by two asterisks (**), follows the first solution. Almost always the first solution is the direct mathematical one and the other is based on one of the tactics discussed in the “Tactics” chapter.

See Important Tactics for an explanation of the symbol ⇒, which is used in several answer explanations.

1. (D) Use TACTIC C2: always solve a proportion by cross multiplying:

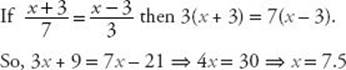
**Whenever a question asks for the value of a single variable, you can backsolve (TACTIC 2). However, you should not have to on a question as easy as this one.

2. (A) a = b2 = (c)2 = 2c2. Since a = 18, 2c2 = 18. So c2 = 9 and c = 3 or c = –3, but only 3 is an answer choice.

**You don’t have to rationalize or simplify . You can just use your calculator.

3. (C)

4. (C) Since vertical angles are congruent (KEY FACT G4), b = 30. Then by KEY FACT G2, a + b + 40 = 180:

a + 30 + 40 = 180 a + 70 = 180 a = 110

5. (C) Since CD = 5 – (–2) = 7, each side of square ABCD must be 7. Sketch the two possibilities for the square and label the four new vertices. Of the five choices, only (–4, 5) could be one of the vertices.

6. (C) Factor both numerators and reduce:

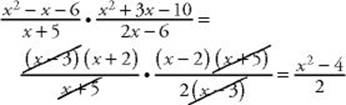
**If you get stuck trying to factor, just plug in a number. If x = 1:

Only choice C equals – when x = 1.

7. (E) In the given week, Susan earned $1,000 – $475 = $525 in commissions, which represented 7% of her sales. So

**Use TACTIC 2: backsolve starting with choice C. 7% of $700 = $49, which is much too small. Eliminate choices A, B, and C and test D or E.

8. (A) Represent the numbers by x and y. Then x + y = 5 and x – y = 5. Add the two equations:

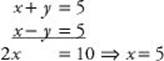
Then 5 + y = 5 y = 0. So the product xy = (5)(0) = 0.

9. (B) f (–5) = –2(–5)2 – 3(–5) = –2(25) + 15 = –50 + 15 = –35

10. (B) If r is the radius of circle O, then by KEY FACTS J4 and J8, a = 2πr and b = πr2. So:

**Use TACTIC 2: backsolve. Calculate the area and circumference for each possible value of the radius.

11. (A)

**Use TACTIC 2: backsolve. Use your calculator to test the answers.

12. (D) By the triangle inequality (KEY FACT H9), x must be greater than 2 and less than 14. Therefore, there are 11 possible integer values of x: 3, 4, 5, . . . , 13.

13. (C) The only even prime is 2, so a = 1. The only prime that is divisible by 7 is 7, so b = 1. No prime is divisible by 9, so c = 0. The primes between 20 and 30 are 23 and 29, so d = 2. Finally, a + b + c + d = 1 + 1 + 0 + 2 = 4.

14. (E) f (x) < 25 x2 – 11 < 25 x2 < 36 –6 < x < 6.

15. (E) By the Pythagorean theorem (KEY FACT H5), (I is true). Now use the trigonometric ratios SOHCAHTOA (KEY FACT M1):

(II and III are true). So statements I, II, and III are true.

**Use TACTIC 3: plug in numbers for a, b, and c, say 3, 4, and 5.

16. (C) Extend a line segment to create a transversal.

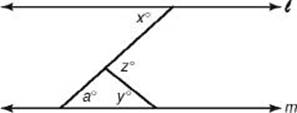
Then by KEY FACT G6, since and m are parallel, a = x. Since the measure of an exterior angle of a triangle is equal to the sum of the measures of the two opposite interior angles (KEY FACT H2):

z = a + y z = x + y x = z – y

**By TACTIC 5, since the given diagram is drawn to scale, you can trust it. The values of x, y, and z appear to be about 40, 45, and 80, respectively. Eliminate choices B and D. A and C are reasonable. However, since it is unlikely that the answer doesn’t involve z, choice C is your best guess.

17. (D) If a = 6 and b = 1, ab is divisible by 6, but b is divisible by neither 2 nor 3. (Statement I is false.)

If a = 2 and b = 3, ab is divisible by 6, but neither a nor b is divisible by 6. (Statement II is false.)

If ab is a multiple of 6, it must be divisible by every divisor of 6, so ab is divisible by both 2 and 3. (Statement III is true.)

Only statement III is true.

18. (A) Use the slope formula (KEY FACT L5) to get the slope of :

By KEY FACT L7, the slope of any line that is perpendicular to is , the negative reciprocal of .

**Use TACTIC 4: draw and line perpendicular to . Clearly, the slope of is negative. Eliminate choices C, D, and E, and guess between A and B.

19. (E)

**Use TACTIC 2: backsolve starting with choice which is too small. Eliminate choices A, B, and C and test choice D or E.

20. (D) If , w, and h are the dimensions of the original rectangular solid, then by KEY FACT K1, the original volume is wh. The new volume is (1.2)(1.2w)(1.25h) = 1.8(wh). So the new volume is 80% more than the original volume.

**Let the original solid be a cube whose edges are 100. Then the new solid has dimensions 120, 120, and 125. The volume of the cube is 1003 = 1,000,000 and the volume of the new rectangular solid is (120)(120)(125) = 1,800,000, which is an increase of 800,000. Finally,

21. (D) By KEY FACT L11, only choices C and D are the equations of a parabola. Eliminate choices A, B, and E. y = x =2 + 3 (choice C) doesn’t pass through (3, 0), whereas y = –x2 + 2x + 3 (choice D) passes through both (0, 3) and (3, 0).

**You can test each answer choice by graphing each equation on a graphing calculator, but that clearly takes more time than the solution presented above.

22. (D) First determine how many 3-digit numbers can be written using only prime digits. Since there are 4 prime digits (2, 3, 5, and 7), if you want to write a 3-digit number using only prime digits, there are 4 choices for each digit. So, by the counting principle (KEY FACT O2), there are 4 × 4 × 4 = 64 3-digit numbers, each of whose digits is prime. Finally, since there are 900 3-digit numbers (the integers from 100–999), by KEY FACT O3, the probability that a 3-digit number chosen at random will have only prime digits is

23. (B) By KEY FACT L8, the slope of the line y = ax + b is a. To find the slope of the line x = cy + d, first solve for y:

Since the slope of the line is the coefficient of x, the slope is . Since parallel lines have equal slopes (KEY FACT L7), .

24. (B) If x = –5, then , which is undefined. In each of the –5–1 = –6 other choices, if you replace x by –5, you will get a real number.

25. (C) First, draw and label triangle ABC.

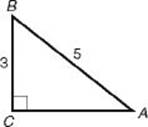
By KEY FACT M1, so let BC = 3 and AB = 5. Then, either by using the Pythagorean theorem (KEY FACT H5) or by recognizing that ABC is a 3-4-5 triangle, note that AC = 4. Therefore,

**If So B = 90° – 36.87° = 53.13°, and sin B = sin 53.13° = 0.8 = .

26. (D) From the given stem-and-leaf plot, you can see that the grades ranged from 58 to 99. Of the 25 grades in the chart, 15 of them are greater than 75 (4 between 76 and 79; 4 in the 80s; and 7 in the 90s). Finally,

27.

The integers that satisfy this inequality are –1, 0, 1, 2, . . . , 13. There are 15 of them.

**Test some numbers: 0, 1, 2, 3 all satisfy the inequality. Keep going: x = 6 works; so does x = 12. That’s already 13 integers that work. Eliminate A and B. Keep going: 13 works, but 14 does not:

So the 14 integers from 0 to 13 all work. That is it unless there are any negative solutions. There is just one: –1, for a total of 15.

28. (E) Assume that in 2003 Hamburger Heaven sold x cheeseburgers at a price of y dollars each. Then in 2004, they sold x + 0.20x = 1.2x cheeseburgers at a price of y + 0.10y = 1.1y dollars each. So the total income in 2003 was xy, whereas in 2004 it was (1.2x)(1.1y) = 1.32xy, an increase of 32%.

**Do exactly what was done above except replace x and y by 100. Assume that in 2003, Hamburger Heaven sold 100 cheeseburgers for $100 each for a total of $10,000. Then in 2004, Hamburger Heaven sold 120 cheeseburgers for $110 each, for a total of $13,200. Finally, $13,200 is $3,200 more than $10,000, an increase of

29. (C) Draw in Also draw perpendicular to intersecting at V.

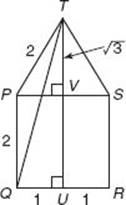
Since PVT is a 30-60-90 right triangle, by KEY FACT H8, PV = QU = 1, and TV = . So TU = 2 + . Now use the Pythagorean theorem in TUQ:

30. (B) By KEY FACT E2, a quadratic equation has real solutions if and only if its discriminant is greater than or equal to 0. In the equation x2 + 5x + k = 0, the discriminant, D, is b2 – 4ac, where a = 1, b = 5, and c = k. So D = 52 – 4(1)k = 25 – 4k. Then:

The largest integer value of k for which k 6.25 is 6.

**You can use a graphing calculator to backsolve. For example, to test choice C, graph the parabola y = x2 + 5x + 7. Since the graph doesn’t cross the x-axis, the equation x2 + 5x + 7 = 0 does not have real solutions. Eliminate choices C, D, and E and test choice B. It works.

31. (E) To write the equation of a line, you need to know a point on the line and the slope of the line. Here, the point is (3, 6). By the slope formula (KEY FACT L5), the radius drawn from the center (0, 2) to the point (3, 6) has slope . By KEY FACT J11, the tangent line is perpendicular to the radius and so by KEY FACT L7, the slope of the tangent line is . Finally, using the point-slope formula for a line (KEY FACT L9), y – y1 = m(x – x1), you get:

**Use TACTIC 4: make a quick sketch of the circle and the line, , tangent to the circle at (3, 6). Since the slope of is clearly negative, you can eliminate choices A, B, and D. If your sketch is good, you can see that the y-intercept is less than 10, so you can eliminate choice C as well.

32. (B) Use the counting principle, KEY FACT O2. There is 1 way to place Bob and 2 ways to place Ed. After that, Al can be placed in one of the 3 remaining spots, followed by Carol, who can stand in one of the other 2 spots. Finally, there is only 1 spot left for Diane. The total number of ways is 1 × 2 × 3 × 2 × 1 = 12.

**List the possibilities. First put Al in the middle and put Ed at the front of the line:

EBACD ECABD EDABC
EBADC ECADB EDACB

Clearly, there will be 6 more possibilities with Ed at the back of the line, so there are a total of 12 ways for the five people to line up.

33. (B) By KEY FACT E3, if ax2 + bx + c = 0, the sum of the roots is and the product of the roots is In choice B, and None of the other choices works.

34. (B) Adam works at the rate of Similarly, Matthew’s rate of work is Together they can mow yards in one hour. Finally:

So when working together, the time required for Adam and Matthew to mow the lawn is:

  hours=1 hour and 52.5 minutes = 112.5 minutes

If you get stuck on a problem like this, don’t omit it
**Use TACTIC 8: and at least eliminate the absurd choices. Since Adam can mow the lawn in 3 hours, or 180 minutes, obviously working together will take less time. Eliminate choice E. If each boy could mow the lawn in 3 hours, together they would take 1.5 hours, or 90 minutes. Eliminate choice A and guess among choices B, C, and D.

35. (C) Let WZ = 1. Then the perimeter of square WXYZ is 4. Since WZY is a right isosceles triangle, by KEY FACT H7, the length of hypotenuse is . However, is also a diameter of the circle, as is in the diagram below. Since EF = AB, the perimeter of square ABCD is 4. Finally the ratio of the perimeters of the two squares .

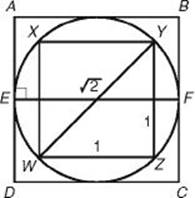
**Use TACTIC 8: eliminate absurd choices. Since the perimeter of square ABCD is greater than the perimeter of square WXYZ, the ratio must be greater than 1. So you can eliminate choices D and E. Also, 2 is almost 3. From the diagram, is clearly less than 2 times as long as . So the perimeter of ABCD is less than 2 times the perimeter of WXYZ. Eliminate choices A and B as well.

36. (B) f (g (x)) = f (x2 – 5) = |(x2 – 5) + 1| = |x2 – 4|

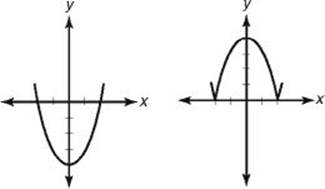
By KEY FACT N4, the graph of y = x2 – 4 is the parabola above left, which is the parabola y = x2 shifted 4 units down. The graph of y = |x2 – 4| (above right) results from reflecting the negative portion of the graph on the left in the x-axis.

**Test some values: if y = |x2 – 4|, then when x = 0, y = 4. Only choices B and C pass through (0, 4). When x = 2, y = 0 and of choices B and C, only B passes through (2, 0).

37. (B) First, expand (sin + cos )2:

 (sin + cos )2 = (sin + cos )(sin + cos )
 = sin2 + 2 sin cos + cos2

Since by KEY FACT M2 sin2 + cos2 = 1:

 (sin + cos )2 = 1 + 2 sin cos

Similarly, (sin – cos )2 = 1 – 2 sin cos

Finally, add the two expressions:

**Use TACTIC 3: plug in a number. Pick any number for , say 10. Then in one line on your calculator enter (sin 10 + cos 10)2 + (sin 10 – cos 10)2. The answer is 2. To be absolutely sure the answer is B, verify that none of choices C, D, and E equal 2 when = 10.

38. (A) By KEY FACT P2, i75 is equal to ir, where r is the remainder when 75 is divided by 4. Since 75 ÷ 4 = 18.75, the quotient is 18. Then 18 × 4 = 72 and 75 – 72 = 3. So the remainder is 3.

Therefore, i75 = i3 and (–i)75 = (–1)75 (i)75 = (–1)(i)3 = –i3
Since i3 = –i, then –i3 = i
Finally, i75 – (–i)75 = i3 – (–i 3) = –i – i = –2i

39. (B) If r is the radius of the circle, then by KEY FACT J8, its area is πr2. Therefore, the area of the shaded region is 3πr2, and the area of the entire rectangle is πr2 + 3πr2 = 4πr2. , the width of the rectangle, is equal to the AB diameter of the circle. So AB = 2r, and the area of

By KEY FACT J4, though, 2πr is exactly the circumference of the circle. So the ratio of AD to the circumference is 1.

**Use TACTICS 5 and 8: trust the diagram and eliminate absurd choices. Clearly isn’t 3 times the circumference, so eliminate choices D and E and guess.

40. (B) By KEY FACT L10, the equation of the circle whose center is (3, –4) and whose radius is 7 is (x – 3)2 + (y + 4)2 = 49. This circle intersects the x-axis at points where the y-coordinate is 0. So, replace y by 0 and solve:

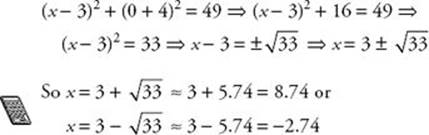
Only I is true.

**Use TACTIC 4: make a quick sketch of the circle. You can immediately see that the circle does not intersect the x-axis at either 0 or 2.74. You cannot be sure that –2.74 is correct, so you have to guess between choices A and B. However, from the sketch it appears that there is an intersection point near –3, so it would make sense to guess B.

41. (C) If s is the side of the cube, then by KEY FACT H7, the length of , a diagonal of the square base, is s. Then by the Pythagorean theorem (KEY FACT H5), in right AEG:

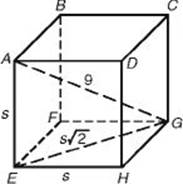
The formula for the total surface area of a cube is A = 6s2 (KEY FACT K2), so A = 6 × 27 = 162.

42. (A) If then x2 – 16 = x2 + 9, which is impossible (x2 – 16 is always less than x2 + 9). So 1 is not in the range of f (x). You can easily verify that each of the other numbers is in the range, but you don’t need to.

43. (A) Since and are radii, OB = OA = 2. By the Pythagorean theorem (KEY FACT H5):

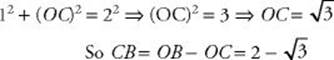
Then by KEY FACT H10, the area of ACB is:

**Use TACTIC 5: trust the diagram. BC is less than one-half of AC, which is 1. So the area of ABC is less than . Clearly, the answer is not C, D, or E. Even choice B is greater than 0.25. Choose A.

44. (E) Use KEY FACT N8. To find f –1(x), write switch x and y, and solve for y :

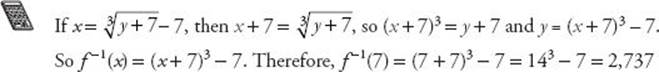
**Since f –1(7) is the number a such that f (a) = 7, you can backsolve: Only

45. (B) If the administrators constitute 27% of the total, then the teachers are 100% – 27% = 73% of the total. So if T is the total number of participants:

  0.73T = 584 T = 584 ÷ 0.73 = 800

Therefore, there are 800 – 584 = 216 administrators at the conference.

**If x represents the number of administrators, then the total number of participants is x + 584. So x is equal to 27% of x + 584:

 x = 0.27(x + 584) = 0.27x + 157.68. So 0.73x = 157.68, and x = 216

**Use TACTIC 2: backsolve. If there are 312 administrators, then there are a total of 312 + 584 = 896 participants. However, 27% of 896 is only 241.92, so 312 is too big. Eliminate choices C, D, and E and test 216. It works.

46. (C) A rhombus is a parallelogram in which all the sides are the same length. By KEY FACT I9, the formula for the area of any parallelogram is A = bh. Sketch the rhombus and draw in the height.

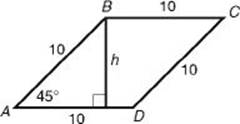
To find h, use the sine ratio (KEY FACT M1):

 

An alternative method of finding h is to use KEY FACT H7, which says that in a 45-45-90 right triangle, the length of each leg is equal to the length of the hypotenuse divided by

Either way, h = 7.07 and the area of the parallelogram is:
A = bh = 10(7.07) = 70.7.

47. (D) To answer this question, you do not have to know what a practical number is (or even what a prime number is for that matter). You just have to understand the logic. To disprove the statement “All roses are red,” you have to produce some (one or more) roses that are not red. Similarly, to show the falseness of the statement “All practical numbers are prime,” you need to show that some (i.e., at least one) practical number is not prime.

48. (D) By KEY FACT K7, the formula for the volume of a pyramid is where B is the area of the base and h is the height. (Remember that this fact is given to you on the first page of the Math 1 test.)

The base of pyramid 1 is a 3-4-5 right triangle, whose area is

The base of pyramid 2 is a square of side 3 whose area is 32 = 9. If h1 and h2 represent the two heights, then:

49. (A) By KEY FACT I2, the sum of the degree measures of the interior angles of pentagon ABCDE is (5 – 2)180° = 3(180°) = 540°. Since the pentagon is regular, the degree measure of each angle is and so mCBF is 180° – 108° = 72°.

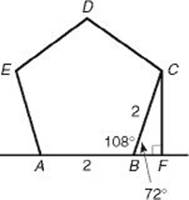
 Then and

Finally, the area of

**If you don’t see how to use trigonometry to answer this question, you still must answer it. It is clear that the length of leg is less than 2, which is the length of hypotenuse . From the diagram, it is clear that BF < 1. So Only choice A is less than 1.

50. (E) Draw in three diagonals that divide the hexagon into six congruent equilateral triangles.

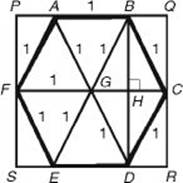
The length of the rectangle is equal to , which is 2. Altitude divides BCG into two 30-60-90 triangles. By KEY FACT H8,

So

Finally, the area of the rectangle is (PQ)(QR) =2.

**Use TACTIC 5: trust the diagram. Clearly PQ, which is 2, is greater than QR, so the area of the rectangle must be less than 4. Eliminate choices B and C. Also, QR is clearly greater than 1, so the area of the rectangle is greater than 2. Eliminate choices A and D.