SAT SUBJECT TEST MATH LEVEL 2
PART 2
![]()
REVIEW OF MAJOR TOPICS
![]()
CHAPTER 1
Functions

1.3 Trigonometric Functions and Their Inverses
![]()
INVERSE TRIG FUNCTIONS
If the graph of any trig function f(x) is reflected about the line y = x, the graph of the inverse (relation) of that trig function is the result. Since all trig functions are periodic, graphs of their inverses are not graphs of functions. The domain of a trig function needs to be limited to one period so that range values are achieved exactly once. The inverse of the restricted sine function is sin–1; the inverse of the restricted cosine function is cos–1, and so forth.

The inverse trig functions are used to represent angles with known trig values. If you know that the tangent of an angle is ![]() , but you do not know the degree measure or radian measure of the angle, tan –1
, but you do not know the degree measure or radian measure of the angle, tan –1 ![]() is an expression that represents the angle between
is an expression that represents the angle between ![]() whose tangent is
whose tangent is ![]() .
.
You can use your graphing calculator to find the degree or radian measure of an inverse trig value.
EXAMPLES
1. Evaluate the radian measure of tan–1 ![]() .
.
Enter 2nd tan ![]() with your calculator in radian mode to get 0.73 radian.
with your calculator in radian mode to get 0.73 radian.
2. Evaluate the degree measure of sin–1 0.8759.
Enter 2nd sin (.8759) with your calculator in degree mode to get 61.15°.
3. Evaluate the degree measure of sec–1 3.4735.
First define x = sec–1 3.4735. If sec x = 3.4735, then cos ![]() . Therefore, enter 2nd cos
. Therefore, enter 2nd cos ![]() with your calculator in degree mode to get 73.27°.
with your calculator in degree mode to get 73.27°.
If “trig” is any trigonometric function, trig(trig–1 x) = x. However, because of the range restriction on inverse trig functions, trig–1(trig x) need not equal x.
4. Evaluate cos (cos–1 0.72).
cos(cos–1 0.72) = 0.72.
5. Evaluate sin–1 (sin 265°).
Enter 2nd sin–1(sin(265)) with your calculator in degree mode to get –85°. This is because –85° is in the required range [–90°,90°], and –85° has the same reference angle as 265°.
6. Evaluate sin ![]() .
.
Let ![]() . Then cos
. Then cos ![]() and x is in the first quadrant. See the figure below.
and x is in the first quadrant. See the figure below.
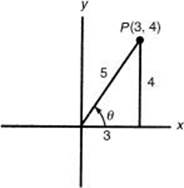
Use the Pythagorean identity sin2x + cos2 x = 1 and the fact that x is in the first quadrant to get sin ![]() .
.
EXERCISES
1. Find the number of degrees in ![]() .
.
(A) –45
(B) –22.5
(C) 0
(D) 22.5
(E) 45
2. Find the number of radians in cos–1(–0.5624).
(A) –0.97
(B) 0.97
(C) 1.77
(D) 2.16
(E) none of these
3. Evaluate tan–1(tan 128°).
(A) –128°
(B) –52°
(C) 52°
(D) 128°
(E) none of these
4. Find the number of radians in cot–1(–5.2418).
(A) –10.80
(B) –5.30
(C) –1.38
(D) –0.19
(E) none of these
5. Which of the following is (are) true?
I. sin–11 + sin–1(–1) = 0
II. cos–11 + cos–1(–1) = 0
III. cos–1 x = cos–1(–x) for all x in the domain of cos–1
(A) only I
(B) only II
(C) only III
(D) only I and II
(E) only II and III
6. Which of the following is a solution of cos3x = ![]() ?
?
(A) 60°
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()