SAT SUBJECT TEST MATH LEVEL 2

PART 2

REVIEW OF MAJOR TOPICS

CHAPTER 1
Functions

1.4 Exponential and Logarithmic Functions

The basic properties of exponents and logarithms and the fact that the exponential function and the logarithmic function are inverses lead to many interesting problems.

The basic exponential properties:

For all positive real numbers x and y, and all real numbers a and b:

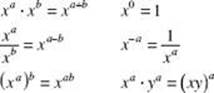
The basic logarithmic properties:

For all positive real numbers a, b, p, and q, and all real numbers x, where a 1 and b 1:

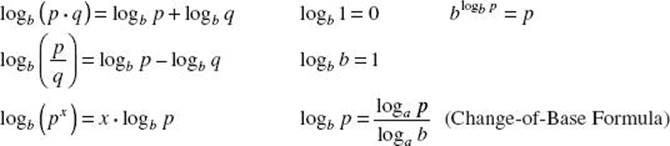
The basic property that relates the exponential and logarithmic functions is:

For all real numbers x, and all positive real numbers b and N, log_b N = x is equivalent to b^x = N. If the base is the number e, ln, the natural logarithm, is used instead of log_e.

By convention, the base is 10 if no base is indicated.

EXAMPLES

1. Simplify x^n–1 · x²ⁿ · (x^2–n)²

This is equal to x^n–1 · x²ⁿ · x^4–2n = x^{n–1 + 2n + 4–2n} = xⁿ⁺³.

2. Simplify .

In order to combine exponents using the properties above, the base of each factor must be the same.

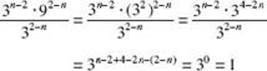
3. If log 23 = z, what does log 2300 equal?

log 2300 = log(23 · 100) = log 23 + log 100 = z + log 10² = z + 2

Note: Examples 3 and 4 can be easily evaluated with a calculator.

4. If ln 2 = x and ln 3 = y, find the value of ln 18 in terms of x and y.

ln 18 = ln(32 · 2) = ln 2 + 2ln 3 = x + 2y

5. Solve for x: log _b(x + 5) = log_b x + log_b 5.

log_b x + log_b 5 = log_b (5x)

Therefore, log(x + 5) = log(5x), which is true only when:

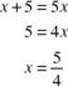
6. Evaluate .

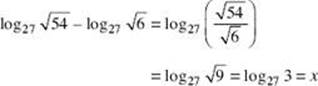
The last equality implies that

27^x= 3
(3³)^x= 3
3^3x= 3¹

Therefore, 3x = 1 and x = .

Thus, .

You could also use the change-of-base formula and your calculator.

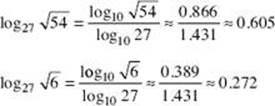
Therefore, .

The graphs of all exponential functions y = b^x have roughly the same shape and pass through point (0,1). If b > 1, the graph increases as x increases and approaches the x-axis as an asymptote as x decreases. The amount of curvature becomes greater as the value of b is made greater. If 0 < b< 1, the graph increases as x decreases and approaches the x-axis as an asymptote as x increases. The amount of curvature becomes greater as the value of b is made closer to zero.

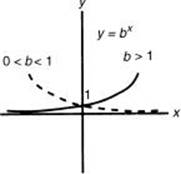
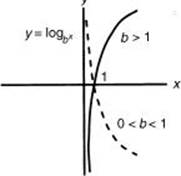
The graphs of all logarithmic functions y = log_b x have roughly the same shape and pass through point (1,0). If b > 1, the graph increases as x increases and approaches the y-axis as an asymptote as x approaches zero. The amount of curvature becomes greater as the value of b is made greater. If 0 < b < 1, the graph decreases as x increases and approaches the y-axis as an asymptote as x approaches zero. The amount of curvature becomes greater as the value of b is made closer to zero.

EXERCISES

1. If x^a· (x^a+1)^a· (x^a)^1–a = x^k, then k =

  (A) 2a + 1

  (B) a + a²

  (C) 3a

  (D) 3a + 1

  (E) a³ + a

2. If log₈ 3 = x · log₂ 3, then x =

  (A)

  (B) 3

  (C) 4

  (D) log₄ 3

  (E) log₈ 9

3. If log₁₀ m = , then log₁₀ 10m² =

  (A) 2

  (B) 2.5

  (C) 3

  (D) 10.25

  (E) 100

4. If log_b 5 = a, log_b 2.5 = c, and 5^x= 2.5, then x =

  (A) ac

  (B)

  (C) a + c

  (D) c – a

  (E) The value of x cannot be determined from the information given.

5. If f (x) = log₂ x, then

  (A)

  (B) 1

  (C)

  (D)

  (E) 0

6. If ln (xy) < 0, which of the following must be true?

  (A) xy < 0

  (B) xy < 1

  (C) xy > 1

  (D) xy > 0

  (E) none of the above

7. log₂ m = and log₇ n = , mn =

  (A) 1

  (B) 2

  (C) 96

  (D) 98

  (E) 103

8. Log₇ 5 =

  (A) 1.2

  (B) 1.1

  (C) 0.9

  (D) 0.8

  (E) – 0.7

9. =

  (A) 1.9

  (B) 2.0

  (C) 2.1

  (D) 2.3

  (E) 2.5

10. If $300 is invested at 3%, compounded continuously, how long (to the nearest year) will it take for the money to double? (If P is the amount invested, the formula for the amount, A, that is available after t years is A = Pe^0.03t .)

  (A) 26

  (B) 25

  (C) 24

  (D) 23

  (E) 22

Answers and Explanations

Exponential and Logarithmic Functions

1. (C)

2. (A)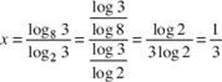

3. (A) log(10m²) = log 10 + 2 log m = 1 + 2 · = 2.

4. (B) b^a = 5, b^c = 2.5 = 5^x , using the relationships between logs and exponents: (b^a )^x = b^ax = 5^x = b^c . Therefore, ax = c and .

5. (B)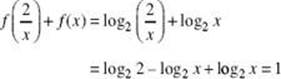

6. (B) Since ln stands for log_e, and e > 1, xy < 1.

* 7. (D) Converting the log expressions to exponential expressions gives and . Therefore, mn = .

* 8. (D) .

* 9. (C)

* 10. (D) Substitute in A = Pe^0.03t to get 600 = 300e^0.03t. Simplify to get 2 = e^0.03t . Then take ln of both sides to get ln 2 = 0.03t and t = . Use your calculator to find that t is approximately 23.