SAT SUBJECT TEST MATH LEVEL 2
PART 2
![]()
REVIEW OF MAJOR TOPICS
![]()
CHAPTER 2
Geometry and Measurement

2.2 Three-Dimensional Geometry
![]()
COORDINATES IN THREE DIMENSIONS
The coordinate plane can be extended by adding a third axis, the z-axis, which is perpendicular to the other two. Picture the corner of a room. The corner itself is the origin. The edges between the walls and the floor are the x- and y-axes. The edge between the two walls is the z-axis. The first octant of this three-dimensional coordinate system and the point (1,2,3) are illustrated below.
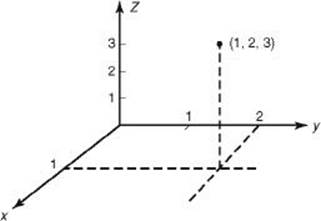
A point that has zero as any coordinate must lie on the plane formed by the other two axes. If two coordinates of a point are zero, then the point lies on the nonzero axis. The three-dimensional Pythagorean theorem yields a formula for the distance between two points (x1,y1,z1) and (x2,y2,z2) in space:
![]()
A three-dimensional coordinate system can be used to graph the variable z as a function of the two variables x and y, but such graphs are beyond the scope of the Level 2 Test.
EXAMPLES
1. The distance between two points in space A (2, y, –3) and B (1, –1, 4) is 9. Find the possible values of y .
Use the formula for the distance between two points and set this equal to 9:
![]()
Square both sides and simplify to get (y + 1)2 = 31. Therefore, y ![]() 4.6 or y
4.6 or y ![]() –6.6.
–6.6.
A sphere is the set of points in space that are equidistant from a given point. If the given point is (a, b, c) and the given distance is r, an equation of the sphere is (x – a)2 + (y – b)2 + (z – c)2 = r2.
2. Describe the graph of the set of points (x, y, z) where
(x – 6)2 + (y + 3)2 + (z – 2)2 = 36.
This equation describes the set of points whose distance from (6, –3, 2) is 6. This is a sphere of radius 6 with center at (6, –3, 2).
If only two of the variables appear in an equation, the equation describes a planar figure. The third variable spans the entire number line. The resulting three-dimensional figure is a solid that extends indefinitely in both directions parallel to the axis of the variable that is not in the equation, with cross sections congruent to the planar figure.
3. Describe the graph of the set of points (x, y, z) where x2 + z2 = 1.
Since y is not in the equation, it can take any value. When restricted to the xz plane, the equation is that of a circle with radius 1 and center at the origin. Therefore in xyz space, the equation represents a cylindrical shape, centered at the origin, that extends indefinitely in both directions along the y-axis.
A solid figure can also be obtained by rotating a plane figure about some line in the plane that does not intersect the figure.
4. If the segment of the line y = –2x + 2 that lies in quadrant I is rotated about the y-axis, a cone is formed. What is the volume of the cone?
As shown in the figure below on the left, the part of the segment that lies in the first quadrant and the axes form a triangle with vertices at (0,0), (1,0), and (0,2). Rotating this triangle about the y-axis generates the cone shown in the figure below on the right.
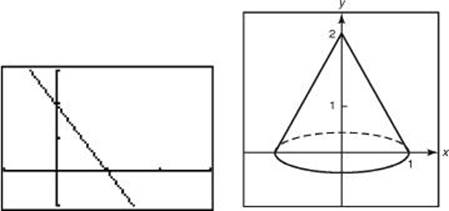
The radius of the base is 1, and the height is 2. Therefore, the volume is
![]()
EXERCISES
1. The distance between two points in space, P (x,–1,–1) and Q (3,–3,1), is 3. Find the possible values of x .
(A) 1 or 2
(B) 2 or 3
(C) –2 or –3
(D) 2 or 4
(E) –2 or –4
2. The point (–4,0,7) lies on the
(A) y-axis
(B) xy plane
(C) yz plane
(D) xz plane
(E) z -axis
3. The region in the first quadrant bounded by the line 3x + 2y = 7 and the coordinate axes is rotated about the x-axis. What is the volume of the resulting solid?
(A) 8 units3
(B) 20 units3
(C) 30 units3
(D) 90 units3
(E) 120 units3