SAT SUBJECT TEST MATH LEVEL 2

PART 2

REVIEW OF MAJOR TOPICS

CHAPTER 3

Numbers and Operations

3.2 Complex Numbers

GRAPHING COMPLEX NUMBERS

A complex number can be represented graphically as rectangular coordinates, with the x -coordinate as the real part and the y -coordinate as the imaginary part. The modulus of a complex number is the square of its distance to the origin. The Pythagorean theorem tells us that this distance is . The conjugate of the imaginary number a + bi is a – bi , so the graphs of conjugates are reflections about the y -axis. Also, the product of an imaginary number and its conjugate is the square of the modulus because (a + bi )(a – bi ) = a ² – b ²i ² = a ² + b².

EXERCISES

1. If z is the complex number shown in the figure, which of the following points could be iz?

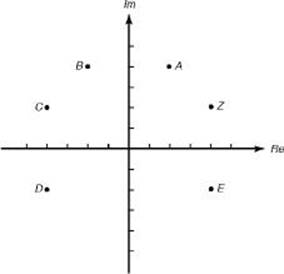
 (A) A

 (B) B

 (C) C

 (D) D

 (E) E

2. Which of the following is the modulus of 2 + i?

 (A)

 (B) 2

 (C)

 (D)

 (E) 5