SAT SUBJECT TEST MATH LEVEL 2

PART 2

REVIEW OF MAJOR TOPICS

CHAPTER 3

Numbers and Operations

3.3 Matrices

DETERMINANTS AND INVERSES OF SQUARE MATRICES

The determinant of an n by n square matrix is a number. The determinant of the 2 by 2 matrix 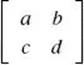is denoted by 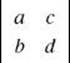, which equals ad – bc.

EXAMPLES

1. Write an expression for the determinant of .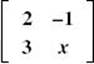

By definition, .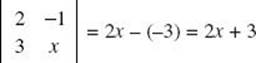

2. Solve for x: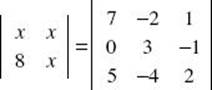

The determinant on the left side is x² – 8x. Use the calculator to evaluate the determinant on the right as 9. This yields the quadratic equation x² – 8x – 9 = 0. This can be solved by factoring to get x = 9 or x = –1.

For larger square matrices, use the graphing calculator to calculate the determinant (2nd/MATRIX/MATH/det). A matrix whose determinant is zero is called singular. If the determinant is not zero, the matrix is nonsingular.

The product of square n by n matrices is a square n by n matrix. An identity matrix I is a square matrix consisting of 1”s down the main diagonal and 0”s elsewhere. The product of n by n square matrices I and A is A. In other words, I is a multiplicative identity for matrix multiplication.

A nonsingular square n by n matrix A has a multiplicative inverse, A^–1, where A^–1A = AA^–1 = I. A^–1 can be found on the graphing calculator by entering MATRIX/NAMES/A, which will return A to the home screen, followed by x^–1 and ENTER.

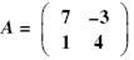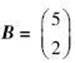3. If and , solve for X when AX = B.

Matrix multiply both sides on the left by A^–1:A^–1AX = A^–1B. This yields IX = X = A^–1B = . The fractional form of the answer can be obtained by keying MATH/ENTER/ENTER.

EXERCISES

1. The determinant of 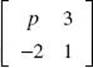is

 (A) p – 6

 (B) p + 6

 (C) 3p – 2

 (D) 3 – 2p

 (E) –6 – p

2. Find all values of x for which .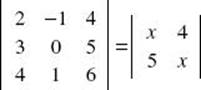

 (A) ±3.78

 (B) ±4.47

 (C) ±5.12

 (D) ±6.19

 (E) ±6.97

3. If 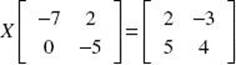, then X =

 (A)

 (B)

 (C)

 (D)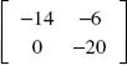

 (E) undefined