Answers and Explanations - Matrices - Numbers and Operations - REVIEW OF MAJOR TOPICS - SAT SUBJECT TEST MATH LEVEL 2

SAT SUBJECT TEST MATH LEVEL 2

PART 2

REVIEW OF MAJOR TOPICS

CHAPTER 3

Numbers and Operations


3.3 Matrices

Answers and Explanations

Addition, Subtraction, and Scalar Multiplication

1. (C) First find the sum of the matrices to the left of the equals sign: . Since the first row of the matrix to the right of the equals sign is (3 2), K must be 4. Since (J M ) is the bottom row, J = –2 and M = 4. Therefore, K + J + M = 6.

2. (E) In order for these matrices to be equal, .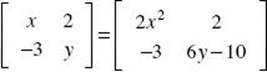

  
Therefore, x = 2x2 and y = 6y – 10. Solving the first equation yields x = 0, and y = 2.

3. (B) To solve for X , first subtract 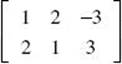from both sides of the equation.

  Then .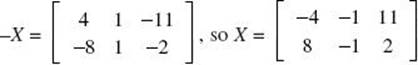

Matrix Multiplication

1. (B) By definition, AB = 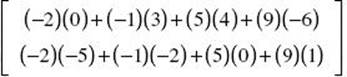= [−37 21]

2. (C) By definition, the first row, second column of the product is (x )(–x ) + (1)(1) = –x2 + 1.

3. (B) X must have as many rows as A has columns, which is 3. X must have as many columns as B does, which is 2.

4. (B) Matrix multiplication is row by column. Since the answer must be a 3 by 1 matrix, the only possible answer choice is B.

Determinants and Inverses of Square Matrices

1. (B) By definition, the determinant of 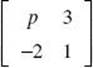is (p )(1) – (3)(–2) = p + 6.

2. (B) Enter the 3 by 3 matrix on the left side of the equation into your graphing calculator and evaluate its determinant (zero). The determinant on the right side of the equation is x2 – 20. Therefore x = ± ±4.47.

3. * (C) To find X , multiply both sides of the equation by on the right. Enter both matrices in your calculator, key the product 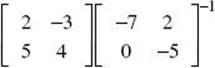on your graphing calculator, and key MATH/ENTER/ENTER to convert the decimal answer to a fraction.

Solving Systems of Equations

1. (B) First, write the system in standard form: . The matrix form of this equation is .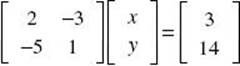

2. * (D) This is the matrix form AX = B of a system of equations. Multiply both sides of the equation by A–1 on the left to get the solution X = 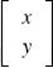= A–1B. Enter the 2 by 2 matrix, A , and the 2 by 1 matrix, B , into your graphing calculator. Return to the home screen and enter A–1B = .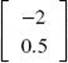