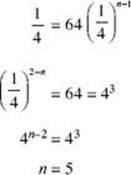SAT SUBJECT TEST MATH LEVEL 2

PART 2

REVIEW OF MAJOR TOPICS

CHAPTER 3

Numbers and Operations

3.4 Sequences and Series

GEOMETRIC SEQUENCES

Another common type of sequence studied at this level is a geometric sequence (or geometric progression). In a geometric sequence the ratio of any two successive terms is a constant r called the constant ratio. The first n terms of a geometric sequence can be denoted by

t₁, t₁r, t₁r², t₁r³, . . . , t₁r^n–1 = t_n

The sum of the first n terms of a geometric series is given by the formula

If there is one term falling between two given terms of a geometric sequence it is called their geometric mean.

EXAMPLES

1. (A) Find the seventh term of the geometric sequence 1, 2, 4, . . . , and
(B) the sum of the first seven terms.

(A)

(B)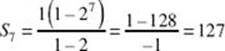

2. The first term of a geometric sequence is 64, and the common ratio is .

For what value of n is ?