SAT SUBJECT TEST MATH LEVEL 2

PART 2

REVIEW OF MAJOR TOPICS

CHAPTER 3

Numbers and Operations

3.4 Sequences and Series

EXERCISES

1. If a₁ = 3 and a_n = n + a_n–1, the sum of the first five terms is

 (A) 17

 (B) 30

 (C) 42

 (D) 45

 (E) 68

2. If a₁ = 5 and find a₃.

 (A) 2.623

 (B) 2.635

 (C) 2.673

 (D) 2.799

 (E) 3.323

3. If the repeating decimal is written as a fraction in lowest terms, the sum of the numerator and denominator is

 (A) 16

 (B) 47

 (C) 245

 (D) 334

 (E) 1237

4. The first three terms of a geometric sequence are The fourth term is

 (A)

 (B)

 (C)

 (D)

 (E)

5. By how much does the arithmetic mean between 1 and 25 exceed the positive geometric mean between 1 and 25?

 (A) 5

 (B) about 7.1

 (C) 8

 (D) 12.9

 (E) 18

6. In a geometric series and . What is r ?

 (A)

 (B)

 (C)

 (D)

 (E)

Answers and Explanations

1. (D) a₂ = 5, a₃ = 8, a₄ = 12, a₅ = 17. Therefore, S₅ = 45

2. * (D) Press 5 ENTER into your graphing calculator. Then enter and press ENTER twice more to get a₃.

3. * (C) The decimal = 0.2 + (0.037 + 0.00037 + 0.0000037 + · · ·), which is 0.2 + an infinite geometric series with a common ratio of 0.01.

  The sum of the numerator and the denominator is 245.

4. (D) Terms are 3^1/4, 3^1/8, 1. Common ratio = 3^–1/8. Therefore, the fourth term is 1 · 3^–1/8 = 3^–1/8 or

5. (C) Arithmetic mean Geometric mean The difference is 8.

6 (D) 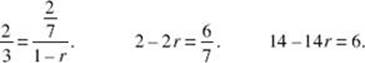Therefore,