SAT Math 1 & 2 Subject Tests

Chapter 3

Arithmetic

You”ve been doing arithmetic as long as you”ve been studying math. This chapter will review basic arithmetic used on the Math Subject Tests, such as factors, multiples, fractions, percents, and exponents. It will also give you some techniques to better assist you in tackling certain arithmetic questions. Don”t forget your calculator!

DEFINITIONS

There are a number of mathematical terms that will be thrown around freely on the test, and you”ll want to recognize and understand them. Here are some of the most common terms:

At the beginning of each chapter in this book, you may see additional definitions that pertain to the material in that chapter. Every time you see such definitions listed, be sure that you know them well. One way to memorize the definitions is to make flash cards for them.

FACTORS AND MULTIPLES

The “factors” of a number are all of the numbers by which it can be divided evenly. ETS sometimes refers to factors as “divisors.” Some questions on the Math Subject Tests will specifically require you to identify the factors of a given number. You may find factorizations useful for solving other questions, even if they don”t specifically talk about factorizations. There are two forms of factorization: plain old factorization and prime factorization.

Factors

The factorization of a number is a complete list of its factors. The best way to compile a list of all of a number”s factors is to write them in pairs, beginning with 1 and the number itself. Then count upward through the integers from 1, checking at each integer to see whether the number you”re factoring is divisible by that integer. If it is, add that integer to the list of factors, and complete the pair.

Remember that the largest
factor of a number is that
number!

Here is the factorization of 60:

Start with 1 and the original number as your first pair and move up (2, 3, 4, etc.) to ensure that you won”t miss any. You”ll know your list is complete when the two columns of factors meet or pass each other. Here, the next integer after 6 that goes into 60 is 10, so you can be sure that the factorization is complete. This is the most efficient way to get a complete list of a number”s factors.

Prime Factors

The other kind of factorization is prime factorization. The prime factorization of a number is the unique group of prime numbers that can be multiplied together to produce that number. For example, the prime factorization of 8 is 2 × 2 × 2. The prime factorization of 30 is 2 × 3 × 5.

Prime factorizations are found by pulling a prime number out of a number again and again until you can”t anymore. The prime factorization of 75, for example, would be found as follows:

 75 =

3 × 25 =

3 × 5 × 5

Notice that it doesn”t matter which prime number you see first as a factor of the original. When you”ve got nothing but prime numbers left, you”re done. Here”s the prime factorization of 78.

 78 =

2 × 39 =

2 × 3 × 13

Because they”re often useful on the Math Subject Tests, you should be able to take prime factorizations quickly.

DRILL

Find the prime factorizations of the following numbers. Answers can be found in Chapter 12.

1. 64 = ________________________________

2. 70 = ________________________________

3. 18 = ________________________________

4. 98 = ________________________________

5. 68 = ________________________________

6. 51 = ________________________________

Prime factorizations are useful in many questions dealing with divisibility. For example:

 What is the smallest number divisible by both 14 and 12 ?

To find the smallest number that both numbers will go into, look at the prime factorizations of 12 and 14: 12 = 2 × 2 × 3, and 14 = 2 × 7, so it”s easy to build the factorization of the smallest number divisible by both 12 and 14. It must contain at least two 2s, a 3, and a 7. That”s 2 × 2 × 3 × 7, or 84. That”s the smallest number you can divide evenly by 12 (2 × 2 × 3) and 14 (2 × 7).

Multiples

ETS also expects you to know the definition of a “multiple.” The multiples of a number are simply all the numbers that are evenly divisible by your original number. An easy way to think of multiples is to recite the times tables for a number. For example, the “positive integer multiples of 6” are simply 6 × 1, 6 × 2, 6 × 3, and so forth, that is, 6, 12, 18…. If ETS asks you for the “fifth positive integer multiple of 6,” that just means 6 × 5, or 30. It”s easy to confuse factors and multiples (ETS hopes you will), so here”s a way to keep the two straight. If you look back at the factorization of 60, you”ll see that there are only 12 factors of 60, which is few. But 60 has as many multiples as you like. So think “factors are few, multiples are many.”

Remember that the
smallest multiple of a
number is that number!

Also notice that factors are smaller than or equal to your original number, whereas multiples are larger than or equal to your original number.

 What is the largest factor of 180 that is NOT a multiple of 15 ?

To answer the question, just make the biggest number you can, using the prime factors of 180. The prime factorization of 180 is 2 × 2 × 3 × 3 × 5. Since 15 is the same as 3 × 5, just make sure your number doesn”t have 3 and 5 as factors. The factor 2 × 2 × 5 may look tempting, but the largest number that fits the bill is 2 × 2 × 3 × 3, or 36.

DRILL

Try the following practice questions. The answers to these questions can be found in Chapter 12.

3. What is the smallest integer divisible by both 21 and 18 ?

(A) 42

(B) 126

(C) 189

(D) 252

(E) 378

7. If ¥x is defined as the largest prime factor of x, then for which of the following values of x would ¥x have the greatest value?

(A) 170

(B) 117

(C) 88

(D) 62

(E) 53

9. If x Ω y is defined as the smallest integer of which both x and y are factors, then 10 Ω 32 is how much greater than 6 Ω 20 ?

(A) 0

(B) 70

(C) 100

(D) 160

(E) 200

EVEN AND ODD, POSITIVE AND NEGATIVE

Some questions on the Math Subject Tests deal with the way numbers change when they”re combined by addition and subtraction, or multiplication and division. The questions usually focus on changes in even and odd numbers, and positive and negative numbers.

Even and Odd Numbers

Even and odd numbers are governed by the following rules:

Division does not have neat rules. For example, 8 divided by 4 is 2 (an even divided by an even can be an even), but 8 divided by 8 is 1 (an even divided by an even can be an odd), and 8 divided by 16 is 0.5 (an even divided by an even may not be an integer). Only integers can be even or odd; fractions and decimals are neither even nor odd.

Positive and Negative Numbers

There are fewer firm rules for positive and negative numbers. Only the rules for multiplication and division are easily stated.

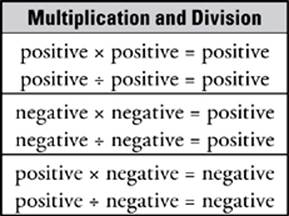
These rules are true for all numbers, because all real numbers except zero—including fractions, decimals, and even irrational numbers—are either positive or negative. Addition and subtraction for positive and negative numbers are a little more complicated—it”s best simply to use common sense.

The one important rule to remember is that subtracting a negative is the same as adding a positive. So,

x − (−5) = x + 5

9 − (−6) = 9 + 6 = 15

If you remember this rule, adding and subtracting negative numbers should be simple.

Your understanding of these rules will be tested in questions that show you simple mathematical operations and ask you about the answers they”ll produce.

DRILL

Try the following practice questions. The answers to these drills can be found in Chapter 12.

15. If n and m are odd integers, then which of the following must also be an odd integer?

I. mn

II.

III. (mn + 1)²

(A) I only

(B) III only

(C) I and II only

(D) I and III only

(E) I, II, and III

18. If c and d are integers and cd < 0, then which of the following statements must be true?

(A) > 0

(B) c + d = 0

(C) c²d > 0

(D) 3cd² ≠ 0

(E) cd(3 + cd) < 0

20. If x is a positive even integer and y is a negative odd integer, then which of the following must be a positive odd integer?

(A) x³y²

(B) (xy + 2)²

(C) xy² − 1

(D) x + y

(E)

DOING ARITHMETIC

This chapter deals with the basic manipulations of numbers: averages, word problems, exponents, and so on. Most of these operations can be greatly simplified by the use of a calculator, so you should practice them with your calculator in order to increase your speed and efficiency. Remember the points about calculator use from Chapter 2, however. If you use your calculator incorrectly, you”ll get questions wrong. If you use it on every question without thinking, it will slow you down. Keep your calculator near at hand, but think before you use it.

The Order of Operations

You remember the Order of Operations, right? PEMDAS (or Please Excuse My Dear Aunt Sally). This is the order you must use to correctly solve an arithmetic problem. PEMDAS stands for Parentheses, Exponents (and roots), Multiplication and Division, Addition and Subtraction.

Left to Right

If you know what you”re
doing, you can compute
left to right or right to
left, but you have to be
careful. For example,
consider the expression
2 − 3 + 4. If you evaluate
this left to right, you do
2 − 3 first, and it becomes
(−1) + 4, which is 3. If you
evaluate from right to left,
you have to interpret it
as −3 + 4, which is 1, and
then 2 + 1 is 3. You can”t
say that 3 + 4 is 7, so it”s
2 − 7, because that gives
you the wrong answer. If
that sounds confusing, just
evaluate left to right and
you”ll be fine..

When using PEMDAS, it”s important to remember that exponents and roots should be calculated from left to right, just as multiplication, division, addition and subtraction should be. You can think of PEMDAS in the following way:

PEMDAS

Parentheses

Exponents and roots

Multiplication and Division

Addition and Subtraction

PEMDAS and Your Calculator

The safest way to do multistep problems like this on a calculator is one step at a time.

On scientific and graphing calculators, it”s possible to type complex expressions into your calculator all at once and let your calculator do the work of grinding out a number. But in order for your calculator to produce the right answer, the expression must be entered in exactly the right way—and that takes an understanding of the order of operations.

For example, the expression 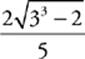would have to be typed into some calculators this way:

On other calculators, it would have to look like the following:

(2(3^3 − 2)^(1/2))/5 =

Any mistake in either pattern would produce an incorrect answer. On other calculators, the equation might have to be typed in in still another way. If you intend to make your calculator do your work for you, check your calculator”s operating manual, and practice. In general, use lots of parentheses to make sure the calculator does the arithmetic in the right order. If you use too many parentheses, the calculator will still give you the right answer, but if you don”t use enough, you may get the wrong answer. And remember, the safest way to use your calculator is one step at a time.

Pretty Print

Some calculators can
display calculations the
way that they would
be written by hand (for
example, using a horizontal
bar with a numerator
above and a denominator
below to represent a
fraction). This feature is
called Pretty Print, and if
you don”t have a calculator,
it may be worth buying
a calculator that has this
feature. It may also be
possible to install an add-on
or change the settings
in your calculator to add
this feature. It”s makes it
easier to check if you”ve
made a mistake, which is
valuable!.

DRILL

Check your PEMDAS skills by working through the following complicated calculations with your calculator (answers can be found in Chapter 12):

1. =

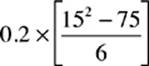2. =

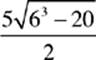3. =

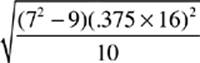4. =

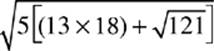5. =

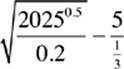FRACTIONS, DECIMALS, AND PERCENTAGES

On arithmetic questions, you will often be called upon to change fractions to decimal numbers, or decimal numbers to percentages, and so on. Be careful whenever you change the form of a number.

You turn fractions into decimals by doing the division represented by the fraction bar.

= 1 ÷ 8 = .125

To turn a decimal number into a fraction, count the number of decimal places (digits to the right of the decimal point) in the number. Then place the number over a 1 with the same number of zeros, get rid of the decimal point, and reduce.

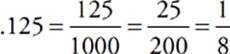
Decimal numbers and percentages are essentially the same. The difference is the percent sign (%), which means “÷ 100.” To turn a decimal number into a percentage, just move the decimal point two places to the right, and add the percent sign.

.125 = 12.5%

To turn percentages into decimal numbers, do the reverse; get rid of the percent sign and move the decimal point two places to the left.

0.3% = 0.003

It”s important to understand these conversions, and to be able to do them in your head as much as possible. Don”t rely on the percent key on your calculator; it”s far too easy to become confused and use it when converting in the wrong direction.

Watch out for conversions between percentages and decimal numbers—especially ones involving percentages with decimal points already in them (like .15%). Converting these numbers is simple, but this step is still the source of many careless errors.

Word-Problem Translation

Most of the common careless errors made in answering math questions are made in the very first step: reading the question. All your skill in arithmetic does you no good if you”re not solving the right problem, and all the power of your calculator can”t help you if you”ve entered the wrongequation. Reading errors are particularly common in word problems.

The safest way to extract equations from long-winded word problems is to translate, word for word, from English to math. All of the following words have direct math equivalents:

Don”t Get Tripped Up

Start writing your multiplication
sign as a dot,
not an ×, if you haven”t
already. Using an × can get
very confusing, especially
if your variable is an x.
Make it easy and don”t trip
yourself up!

Using this table as a guide, you can translate any English sentence in a word problem into an equation. For example:

3. If the bar of a barbell weighs 15 pounds, and the entire barbell weighs 75 pounds, then the weight of the bar is what percent of the weight of the entire barbell?

The question at the end of the problem can be translated into:

15 = • 75

Solve this equation, and the question is answered. You”ll find that x is equal to 20, and 20% is the correct answer.

DRILL

For each of the following exercises, translate the information in English into an equation and solve. The answers to this drill can be found in Chapter 12.

1. 6.5 is what percent of 260?

2. If there are 20 honors students at Pittman High and 180 students at the school in all, then the number of honors students at Pittman High is what percentage of the total number of students?

3. Thirty percent of 40 percent of 25 marbles is how many marbles?

4. What is the square root of one-third of 48?

5. The square root of what positive number is equal to one-eighth of that number?

Word for Word

Use the English to math
conversion chart to
translate each word
into math.

Percent Change

“Percent change” is a way of talking about increasing or decreasing a number. The percent change is just the amount of the increase or decrease, expressed as a percentage of the starting amount.

For example, if you took a $100.00 item and increased its price by $2.00, that would be a 2% change, because the amount of the increase, $2.00, is 2% of the original amount, $100.00. On the other hand, if you increased the price of a $5.00 item by the same $2.00, that would be a 40% increase—because $2.00 is 40% of $5.00. If you ever lose track of your numbers when computing a percent change, just use this formula:

%Change = 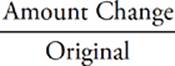× 100

Whenever you work with percent change, be careful not to confuse the amount of the change with the total after you”ve worked out the percent change. Just concern yourself with the original amount and the amount of the increase or decrease. The new total doesn”t matter.

DRILL

Test your understanding of percent change with the following practice questions. The answers to these drills can be found in Chapter 12.

2. A 25-gallon addition to a pond containing 150 gallons constitutes an increase of approximately what percent?

(A) 14.29%

(B) 16.67%

(C) 17.25%

(D) 20.00%

(E) 25.00%

5. The percent decrease from 5 to 4 is how much less than the percent increase from 4 to 5 ?

(A) 0%

(B) 5%

(C) 15%

(D) 20%

(E) 25%

12. Nicoletta deposits $150.00 in her savings account. If this deposit represents a 12 percent increase in Nicoletta”s savings, then how much does her savings account contain after the deposit?

(A) $1,100.00

(B) $1,250.00

(C) $1,400.00

(D) $1,680.00

(E) $1,800.00

Your Calculator Is
Your Friend

Here”s a great place
to test out how you”re
putting equations in your
calculator.

Percent change shows up in many different problem types on the Math Subject Tests—it can be brought into almost any kind of math question. Here”s one of the most common math question types that deals with percent change.

The Change-Up, Change-Down It”s a classic trick question to ask what happens if you increase something by a percent and then decrease it by the same percent, as follows:

9. The price of a bicycle that usually sells for $250.00 is marked up 30 percent. If this new price is subsequently discounted by 30 percent, then the final price of the bicycle is

(A) $200.50

(B) $216.75

(C) $227.50

(D) $250.00

(E) $265.30

Here”s How to Crack It

The easy mistake on this problem type is to assume that the price (after increasing by 30% and then decreasing by 30%) has returned to $250.00, the original amount. Nope! It doesn”t actually work out that way, as you”ll see if you try it step by step. First, you increase the original price by 30%.

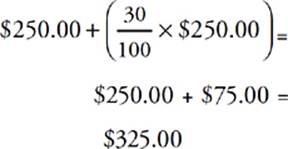
Then, discount this price by 30%.

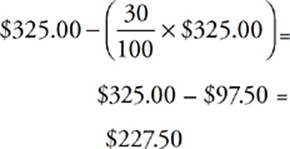
The answer is (C). As you can see, the final amount isn”t equal to the starting amount. The reason for the difference is that you”re increasing the price by 30% of the starting number, and then decreasing by 30% of a different number—the new, higher price. The changes will never be of the same amount—just the same percent. You end up with a number smaller than your starting number, because the decrease was bigger than the increase. In fact, if you”d done the decrease first and then the increase, you would still have gotten the same number, $227.50.

Remember this tip whenever you increase a quantity by a percent and then decrease by the same percent. Your final result will always be a bit smaller than your original amount. The same thing is true if you decrease a quantity by a percent and then increase by the same percent. You”ll get a number a bit lower than your starting number.

REPEATED PERCENT CHANGE

On one common question type you”ll have to work with percent change and exponents together. Occasionally, you”ll be required to increase or decrease something by a percent again and again. Such questions often deal with growing populations or bank accounts collecting interest. Here”s an example:

40. Ruby had $1,250.00 in a bank account at the end of 1990. If Ruby deposits no further money in the account, and the money in the account earns 5 percent interest every year, then to the nearest dollar, how much money will be in the account at the end of 2000 ?

(A) $1,632.00

(B) $1,786.00

(C) $1,875.00

(D) $2,025.00

(E) $2,036.00

Here”s How to Crack It

The easy mistake here is to find 5% of the original amount, which in this case would be $62.50. Add $62.50 for each of the ten years from 1990 to 2000 and you”ve got an increase of $625.00, right? Wrong. That would give you a final total of $1,875.00, but that”s not the right answer. Here”s the problem—the interest for the first year is $62.50, which is 5% of $1,250. But that means that now there”s $1,312.50 in the bank account, so the interest for the second year will be something different. As you can see, this could get messy.

Remember to Keep an Eye Out for Traps

Notice that $1,875.00 is in the answers. Remember that ETS loves to put in numbers that look familiar to you. You”ll see partial answers; you”ll see answers to a question that wasn”t even asked. A test question numbered 40 is going to be a difficult one. Always remember to keep an eye out for answers that you can eliminate.

Here”s the easy way. The first year”s interest can be computed like any ordinary percent change, by adding the percent change to the original amount.

$1,250.00 + ( × $1,250.00) = total after one year

But there”s another way to write that. Just factor out the $1,250.00.

$1,250.00 × (1 + ) = total after one year

$1,250.00 × (1.05) = total after one year

You can get the total after one year by converting the percent change to a decimal number, adding 1, and multiplying the original amount by this number. To get the total after two years, just multiply by that number again.

$1,250.00 × (1.05) × (1.05) = total after two years

And so on. So, to figure out how much money Ruby will have after 10 years, all you have to do is multiply her original deposit by 1.05, 10 times. That means multiplying Ruby”s original deposit by 1.05 to the 10th power.

$1,250.00 × (1.05)¹⁰ = total after 10 years

$1,250.00 × 1.629 = total after 10 years

  $2,036.25 = total after 10 years

So, to the nearest dollar, Ruby will have $2,036.00 after 10 years. The answer is (E).

There”s a simple formula you can use to solve repeated percent-increase problems.

Final amount = Original × (1 + Rate)^{number of changes}

The formula for repeated percent-decrease problems is almost identical. The only difference is that you”ll be subtracting the percentage change from 1 rather than adding it.

Final amount = Original × (1 − Rate)^{number of changes}

Just remember that you”ve got to convert the rate of change (like an interest rate) from a percentage to a decimal number.

Here”s another one. Try it yourself, and then check the explanation below.

43. The weight of a bar of hand soap decreases by 2.5 percent each time it is used. If the bar weighs 100 grams when it is new, what is its weight in grams after 20 uses?

(A) 50.00

(B) 52.52

(C) 57.43

(D) 60.27

(E) 77.85

Here”s How to Crack It

You”ve got all of your starting numbers. The original amount is 100 grams, and the rate of change is 2.5%, or 0.025 (remember to subtract it, because it”s a decrease). You”ll be going through 20 decreases, so the exponent will be 20. This is how you”d plug these numbers into the formula.

The answer is (D). This is an excellent example of a question type that is difficult if you”ve never seen it before, and easy if you”re prepared for it. Memorize the repeated percent-change formulas and practice using them.

To Memorize or Not to Memorize?

So, at this point, you”re probably starting to get nervous about how many formulas we”re giving you and how much you have to memorize. But remember: We”re also showing you how to get there. Formulas are designed to save you time. If you ever can”t remember a formula, you can still figure out how to do the problem. Notice for repeated percent change, you can do it the long way and still get to the right answer accurately. And don”t forget your techniques like approximation and POE … and there”s still more to come!

DRILL

Try the following practice questions. The answers to these drills can be found in Chapter 12.

35. At a certain bank, savings accounts earn 5 percent interest per year. If a savings account is opened with a $1,000.00 deposit and no further deposits are made, how much money will the account contain after 12 years?

(A) $ 1,333.33

(B) $ 1,166.67

(C) $ 1,600.00

(D) $ 1,795.86

(E) $12,600.00

40. In 1900, the population of Malthusia was 120,000. Since then, the population has increased by exactly 8 percent per year. What was the population in the year 2000 ?

(A) 216,000

(B) 2,599,070

(C) 1,080,000

(D) 5.4 × 10⁷

(E) 2.6 × 10₈

43. In 1995, Ebenezer Bosticle created a salt sculpture that weighed 2,000 pounds. If this sculpture loses 4 percent of its mass each year to rain erosion, what is the last year in which the statue will weigh more than 1,000 pounds?

(A) 2008

(B) 2009

(C) 2011

(D) 2012

(E) 2013

AVERAGES

The tests use averages in a variety of question types. Remember, the average is the sum of all the values divided by the number of values you”re adding up. Looking at this definition, you can see that every average involves three quantities: the total, the number of things being added, and the average itself.

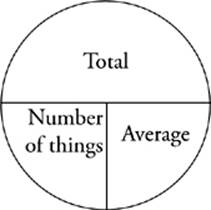
The chart above is called an average pie. It”s The Princeton Review way of organizing the information found in an average problem. Cover up the “average” section with your thumb. In order to find the average, you divide the total by the “number of things.” Now cover up the “number of things” section. You can find it by dividing the total by the average. Finally, you can find the total by multiplying the number of things by the average.

Ways to Remember

Remember that in order
to find the average, you
divide the total by the
number of things. Think of
the horizontal line in the
average pie as one big
division bar!

When you run into an average in a Math Subject Test question, you”ll be given two of the three numbers involved. Usually, solving the problem will depend on your supplying the missing number in the average pie.

DRILL

Test your understanding of averages with the following questions. The answers to these drills can be found in Chapter 12.

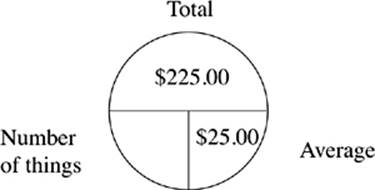
1. People at a dinner paid an average of $25.00 each. The total bill for dinner was $225.00.

What else do you know? ______________

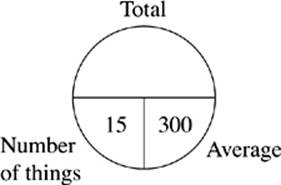
2. The average fruit picker on Wilbury Ranch picked 300 apples on Tuesday. There are 15 fruit pickers at Wilbury Ranch.

What else do you know? _______________

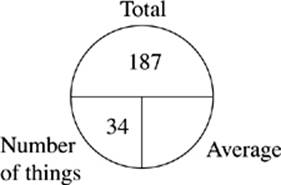
3. If the 34 students in the chess club lie down end to end, they would form a line 187 feet long.

What else do you know? _______________

The average pie becomes most useful when you”re tackling a multiple-average question—one that requires you to manipulate several averages in order to find an answer. Here”s an example:

32. Sydney”s average score on the first 5 math tests of the year was 82. If she ended the year with a math test average of 88, and a total of 8 math tests were administered that year, what was her average on the last three math tests?

(A) 99.5

(B) 98.75

(C) 98.0

(D) 96.25

(E) 94.0

Here”s How to Crack It

In this question, there are three separate averages to deal with: Sydney”s average on the first five tests, her average on the last three tests, and her final average for all eight. In order to avoid confusion, take these one at a time. Draw the first average pie.

Average Pies and Variables, Never the Twain Shall Meet

There should never be a variable in your average pie. You will always be given two of the three numbers you need in your pie. If you can”t find two of the three numbers, that means you”ve missed a step somewhere.

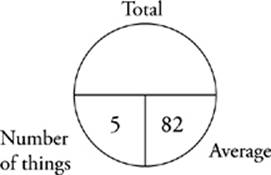
You have the number of things and the average, so you can find the total. You know that Sydney”s total for the first test is 410. Fill in that information and draw another pie. For your second pie, the question tells you that Sydney”s average on all 8 tests was 88, so you can multiply those numbers to find the total of her 8 scores, or 704. Fill in your second average pie below.

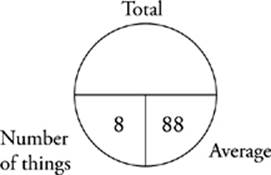
Since you know the total of all 8 tests and the total of the first 5 tests, you can figure out the total of the last three tests:

704 − 410 = 294

Draw one last pie, using the information that you have:

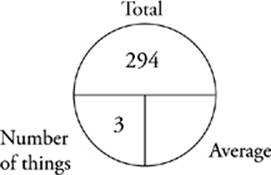
As it turns out, Sydney averaged a 98 on her last three math tests; so the answer is (C).

Multiple-average questions are never terribly difficult. Just draw an average pie every time you see the word average in the question. Organization is everything on these questions. It”s easy to make careless errors if you get your numbers scrambled, so make sure you label the parts of the average pie. Notice that you can always add or subtract totals and numbers of things, but you can never add or subtract averages.

DRILL

Try these problems. The answers can be found in Chapter 12.

33. At a charity fund-raiser, the average of the first 19 donations is $485.00. In order for the average of the first 20 donations to be $500.00, what must the amount of the twentieth donation be, in dollars?

(A) $300

(B) $515

(C) $650

(D) $785

(E) $800

35. During the first 20 days of September, the Tribune received an average of 4 complaint letters per day. During the last 10 days of September, the Tribune received an average of 7 complaint letters per day. What was the Tribune”s average number of complaint letters per day for the entire month of September?

(A) 5.0

(B) 5.33

(C) 5.67

(D) 6.0

(E) 6.25

36. Over a year, Brendan sold an average of 12 umbrellas per day on rainy days, and an average of 3 umbrellas per day on clear days. If the weather was rainy one day in five, and this was not a leap year, what was Brendan”s average daily umbrella sales for the year?

(A) 4.8

(B) 5.2

(C) 6.75

(D) 7.3

(E) 9.0

EXPONENTS

An exponent is a simple way of expressing repeated multiplication. You can think of 5³, for example, as 5 × 5 × 5. In this exponential expression, 5 is referred to as the “base,” while 3 is the “exponent.” Sometimes a third number is also present, called a “coefficient.” In the expression 4b², bis the base, 2 is the exponent, and 4 is the coefficient. Here, b is being squared, but the coefficient, 4, is not affected by the exponent.

For certain Math Subject Test questions, you”ll need to do some algebraic calculations using exponents. To work with exponents in equations, you just need to remember a few basic rules.

Rules Come from Somewhere

If you ever forget the rules of exponents, remember that you can always expand and cancel. So if you”re ever unclear, write it out. Here”s a great example:

x² • x⁴ = (x • x)(x •x •x • x)

You have six x”s. So the answer is x⁶.

This also works with dividing:

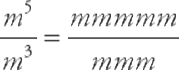
Now cancel and you get mm or m².

You never have to stress about forgetting your rules. They make it easier to get through the problem more quickly, but if you forget, there”s always another way!

Multiplying Exponents When Bases Are the Same

Exponential terms can be multiplied when their bases are the same. Just leave the bases unchanged and add the exponents.

n³ × n⁵ = n⁸ 3 × 3⁴ = 3⁵

Coefficients, if they are present, are multiplied normally.

2b × 3b⁵ = 6b⁶ c³ × 6c⁵ = 3c⁸

Dividing Exponents When Bases Are the Same

Exponential terms can also be divided when their bases are the same. Once again, the bases remain the same, and the exponents are subtracted.

x⁸ ÷ x⁶ = x² 7⁵ ÷ 7 = 7⁴

Coefficients, if they are present, are divided normally.

6b⁵ ÷ 3b = 2b⁴ 5a⁸ ÷ 3a² = a⁶

Multiplying and Dividing Exponents When Exponents Are the Same

There”s one special case in which you can multiply and divide terms with different bases—when the exponents are the same. In this case you can multiply or divide the different bases. Then the bases change and the exponents remain the same.

For multiplication:

And for division:

If exponential terms have different bases and different exponents, then there”s no way to combine them by adding, subtracting, dividing, or multiplying.

Adding and Subtracting When Bases and Exponents Are the Same

Terms with exponents can be added or subtracted only when they have the same base and exponent.

If they don”t have the same base and exponent, exponential terms can never be combined by addition or subtraction.

Raising Powers to Powers

When an exponential term is raised to another power, the exponents are multiplied.

If there is a coefficient included in the term, then the coefficient is also raised to that power.

Using these rules, you should be able to manipulate exponents wherever you find them.

ROOTS

Roots are exponents in reverse. For example, 4 × 4 = 16. That means that 4² = 16. It also means that = 4. Square roots are by far the most common roots on the Math Subject Tests. The square root of a number is simply whatever you would square to get that number.

A Horse of a
Different Color

Square roots are sometimes
called roots of the
second power. It”s yet
another way ETS tries
to throw you. It makes
a simple concept sound
very complicated. But you
know better!

You may also encounter other roots: cube roots, fourth roots, fifth roots, and so on. Each of these roots is represented by a radical with a number attached, like , which means the cube root of x. Roots of higher degrees work just as square roots do. The expression , for example, equals 3—the number that you”d raise to the 4th power to get 81. Similarly, is the number that, raised to the 5th power, equals 32—in this case, 2.

When the number under a radical has a factor whose root is an integer, then the radical can be simplified. This means that the root can be pulled out. For example, is equal to . Because 16 is a perfect square, its root can be pulled out, leaving the 3 under the radical sign, as 4. That”s the simplified version of .

The Principal Idea

Remember how both 2 and −2 raised to the 4th power equal 16? Well, for the Math Subject Tests, a radical refers only to the principal root of an expression. When there is only one root, that”s the principal root. An example of this is . The only root of this expression is 3. When you have both a positive and a negative root, the positive root is considered to be the principal root and is the only root symbolized by the radical sign. So, even though 2⁴ = 16 and (−2)² = 16, means 2 only, and not −2.

Working with Roots

The rules for manipulating roots when they appear in equations are the same as the rules for manipulating exponents. Roots can be combined by addition and subtraction only when they are roots of the same order and roots of the same number.

Roots can be multiplied and divided freely as long as all the roots are of the same order—all square roots, or all cube roots, and so on. The answer must also be kept under the radical.

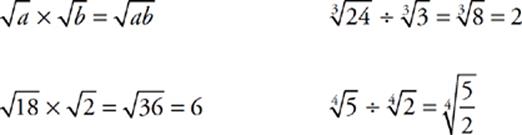
Be sure to memorize these rules before working with roots.

Fractional Exponents

A fractional exponent is a way of raising a number to a power and taking a root of the number at the same time. The number on top is the normal exponent. The number on the bottom is the root—you can think of it as being in the “root cellar.”

So, in order to raise a number to the power, you would square the number and then take the cube root of your result. You could also take the cube root first and then square the result—it doesn”t matter which one you do first, as long as you realize that 2 is the exponent and 3 is the order of the root.

Remember that an exponent of 1 means the number itself, so is equal to , the square root of x to the first power. Knowing this will help you handle roots with your calculator. For example, can be entered into your calculator as 17^(1/3).

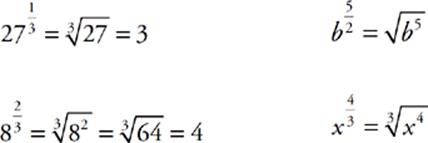
Calculator Tip

Some scientific calculators
have an exponent key
that looks like y^x, x^y, or xⁿ
instead of ^.

SPECIAL EXPONENTS

There are some exponents on the Math Subject Tests that you”ve got to treat a little differently. Below are some unusual exponents with which you should be familiar.

Zero

Any number (except zero) raised to the power of zero is equal to 1, no matter what you start with. It”s a pretty simple rule.

One

Any number raised to the first power is itself—it doesn”t change. In fact, ordinary numbers, written without exponents, are numbers to the first power. You can think of them as having an invisible exponent of 1. That”s useful when using the basic exponent rules you”ve just reviewed. It means that (x⁴ ÷ x) can be written as (x⁴ ÷ x¹), which can prevent confusion when you”re subtracting exponents.

Negative Exponents

Treat a negative exponent exactly like a positive exponent, with one extra step. After you have applied the exponent, flip the number over—that is, you turn the number into its reciprocal.

The negative sign works the same way on fractional exponents. First you apply the exponent as you would if it were positive, and then flip it over.

MORE IMPORTANT EXPONENT STUFF

There are a few important things to remember about the effects of exponents on various numbers:

· A positive number raised to any power remains positive. No exponent can make a positive number negative.

· A negative number raised to an odd power remains negative.

· A negative number raised to an even power becomes positive.

In other words, anything raised to an odd power keeps its sign. If a³ is negative, then a is negative; if a³ is positive, then a is positive. A term with an odd exponent has only one root. For example, if a³ = −27, there”s only one value of a that makes it true: a = −3.

On the other hand, anything raised to an even power becomes positive, regardless of its original sign. This means that an equation with an even exponent has two roots. For example, if b² = 25, then b has two possible values: 5 and −5. It”s important to remember that two roots exist for any equation with an even exponent (the only exception is when b² = 0, in which case b can equal only 0, and b² has only one root).

One last thing to remember—since any real number becomes positive when raised to an even exponent, certain equations will have no real roots. For example, the equation x² = −9 has no real roots. There”s no integer or fraction, positive or negative, that can be squared to produce a negative number. In this equation, x is said to be an imaginary number. The equation is considered to have no real solution.

Drill

In the following exercises, find the roots of the exponential expression given. Specify whether each expression has one root, two roots, or no real roots. The answers to these drills can be found in Chapter 12.

1. b³ = 27; b =

2. x² = 121; x =

3. n⁵ = 32; n =

4. c² = 10; c =

5. x⁴ = 81; x =

6. x³ = −8; x =

7. d⁶ = 729; d =

8. n⁰ = 1 (for n ≠ 0); n =

Now try some multiple-choice questions. In the following exercises, expand the exponential expressions. Where the bases are numbers, find the numerical values of the expressions. The answers to these drills can be found in Chapter 12.

1. =

(A) 2.52

(B) 3.64

(C) 8.00

(D) 16.00

(E) 18.67

2. =

(A)

(B) −

(C)

(D)

(E)

3. =

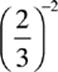(A) 2.25

(B) 1.67

(C) 0.44

(D) −1.50

(E) −0.44

4. =

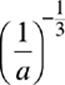(A) −

(B)

(C)

(D) −a³

(E)

5. =

(A) 2.92

(B) 5.00

(C) 6.25

(D) 8.67

(E) 11.18

6. =

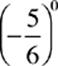(A) −1.2

(B) −0.8

(C) 0.0

(D) 1.0

(E) 1.2

Summary

· Factors are numbers that divide into your original number. Multiples are numbers that your original number divides into.

· Factors are smaller than or equal to your original number.

· Multiples are larger than or equal to your original number.

· Make sure that you have a good grasp of PEMDAS and the rules involving even, odd, positive, and negative numbers:

· even ± even = even

· even ± odd = odd

· odd ± odd = even

· even × even = even

· even × odd = even

· odd × odd = odd

· positive × or ÷ positive = positive

· negative × or ÷ negative = positive

· positive × or ÷ negative = negative

· If you have a question that asks for the average, mean, or arithmetic mean, use the average pie:

· There are two formulas for percent change:

· The basic formula for percent change is:

%Change = 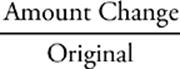× 100

· The formula for repeated percent change is: Final = Original × (1 ± Rate)^{# of changes}. If it”s a repeated percent increase, you add Rate. If it”s a decrease, you subtract Rate.

· Special exponents:

· Any number, except 0, raised to the 0 power is 1.

· Raising a number to the first power does not change the number.

· A negative exponent means take the reciprocal of the number (divide 1 by the number), and then apply the exponent.

· Fractional exponents are a way of writing exponents and roots together: The top of the fraction is the exponent and the bottom of the fraction is the root.

· For exponents and roots, if you”re adding or subtracting, the bases (what”s under the root sign) must be the same.