SAT Math 1 & 2 Subject Tests

Chapter 5

Plane Geometry

ETS uses the term “plane geometry” to refer to the kind of geometry that is commonly tested on the SAT—questions about lines and angles, triangles and other polygons, and circles. Simply put, plane geometry is the study of two-dimensional figures in a plane. Don”t confuse plane geometry with coordinate geometry, which involves plotting ordered pairs of numbers on a grid, referred to as the “coordinate plane.”

Questions testing plane geometry appear almost exclusively on the Math Level 1 Subject Test. About 20 percent of the questions on the Math Level 1 concern plane geometry. None of the questions on the Math Level 2 will focus on plane geometry, but you”ll need the tools in this chapter to answer some Math Level 2 questions about coordinate geometry, solid geometry, and trigonometry.

Definitions

Here are some geometry terms that appear on the Math Subject Tests. Make sure you”re familiar with them. If the meaning of any of these vocabulary words keeps slipping your mind, add that word to your flash cards.

BASIC RULES OF LINES AND ANGLES

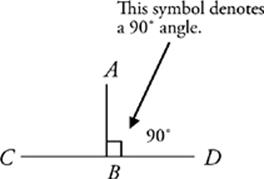
A right angle has a measure of 90˚. The angles formed by perpendicular lines are right angles. In the figure above, we see that AB ⊥ CD. The symbol ⊥ means “perpendicular.”

Approximation

In Chapter 2, we discussed approximation, and how it can help you use POE to eliminate answer choices that are too big or too small. Unless ETS indicates that a figure is NOT drawn to scale, you can assume it is and use approximation to eliminate impossible lengths, angles, and areas (such as shaded regions). If a figure is not drawn to scale, you should redraw it according to any information ETS gives you. If, on the other hand, no figure is given at all, you”ll want to make sure to draw one yourself so you can solve the problem more easily. Try to make your picture match the information given as closely as possible—you may be able to approximate and eliminate answer choices that are the wrong size.

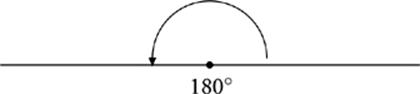
An angle opened up into a straight line (called a “straight angle”) has a measure of 180˚. If a number of angles makes up a straight line, then the measures of those angles add up to 180˚.

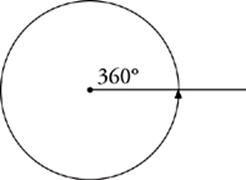
Any line rotated through a full circle moves through 360˚. If a group of angles makes up a full circle, then the measures of those angles add up to 360˚.

When two lines cross, opposite angles are equal (these are called “vertical angles”). Adjacent angles form straight lines and, therefore, add up to 180˚.

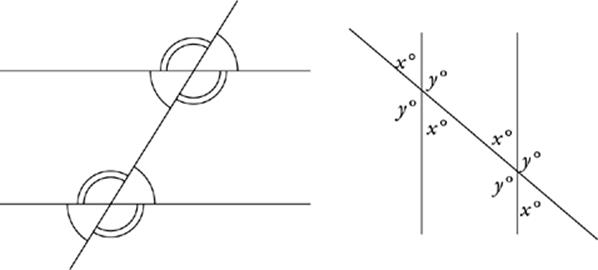
Fred”s theorem: When parallel lines are crossed by a third line, two kinds of angles are formed—little angles and big angles. All of the little angles are equal, all of the big angles are equal, and any little angle plus any big angle equals 180˚. Why is it called “Fred”s” theorem? Well, we had to call it something and Fred is as good a name as any.

ETS will sometimes use the parallel symbol as well. For example, AC DE means that AC is parallel to DE. Think of the two l”s in parallel to help you remember this.

Likewise, the symbol for perpendicular is , as in GH JK. It”s easy to remember this symbol because it looks like perpendicular lines: two lines meeting to form right angles.

What”s with All the Symbols?

In geometry questions ETS sometimes will write out the geometric phrase “line segment AB.” Sometimes, however, the test writers will use only geometric symbols or write these kinds of things in “code form.” So line segment AB would be AB.

This is just one more way ETS tries to confuse you or throw you off your game. You”ll notice symbols and their explanations in sidebars throughout the book to remind you what they mean. Make sure you”re familiar with them!

DRILL

In the following exercises, find each measure. The answers to these drills can be found in Chapter 12.

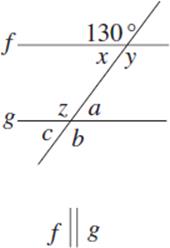
1. x _____________ a _____________
y _____________ b _____________
z _____________ c _____________

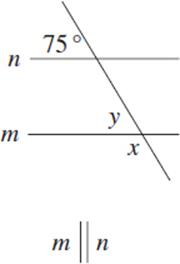
2. x _____________
y _____________

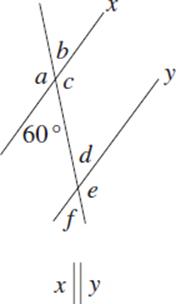
3. a _____________ d _____________
b _____________ e _____________
c _____________ f _____________

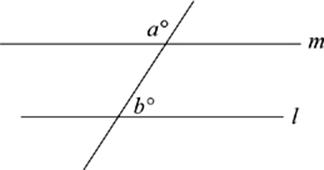
8. If line l and line m are parallel, then a + b =

(A) 90°

(B) 180°

(C) 270°

(D) 360°

(E) It cannot be determined from the information given.

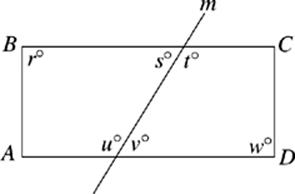
13. If line m intersects rectangle ABCD as shown, then which of the following is equal to t ?

(A) v

(B) w

(C) r + s

(D) w − v

(E) r + w − s

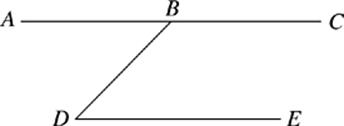
16. If AC DE, then which of the following is the difference between the degree measures of ∠DBC and ∠BDE ?

(A) 0°

(B) 45°

(C) 90°

(D) 180°

(E) It cannot be determined from the information given.

TRIANGLES

Triangles appear in the majority of plane geometry questions on the Math Subject Tests. What”s more, triangle techniques are useful in solving questions that don”t obviously relate to triangles, such as coordinate geometry and solid geometry questions. The following rules are some of the most important in plane geometry.

The Rule of 180º

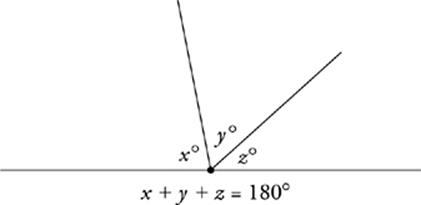
For starters, the three angles of any triangle add up to 180˚. This rule helps to solve a great many plane geometry questions.

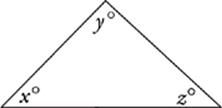
x + y + z = 180º

The Proportionality of Triangles

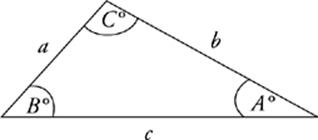
A < B < C

a < b < c

In a triangle, the smallest angle is always opposite the shortest side; the middle angle is opposite the middle side; and the largest angle is opposite the longest side. If a triangle has sides of equal length, then the opposite angles will have equal measures.

Opposite Side? Huh?

If you have trouble figuring
out which side is opposite
a certain angle in a
triangle, remember this
simple rule: The opposite
side is the side that
doesn”t touch the angle
you”re talking about.

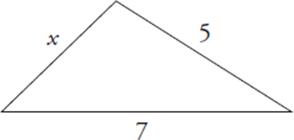
The Third Side Rule

The Third Side Rule: The length of any side of a triangle must be between the sum and the difference of the lengths of the other two sides.

2 < x × 12

Sneaky ETS!

The Third Side Rule is commonly
used to create tricky
triangle questions.

Isosceles Triangles

An isosceles triangle has two equal sides and two equal angles.

Isosceles and the
Third Side

Watch out for questions
that employ the Third Side
Rule in isosceles triangles.

Equilateral Triangles

An equilateral triangle has three equal sides and three equal angles. Each angle has a measure of 60˚.

DRILL

The answers to these drills can be found in Chapter 12.

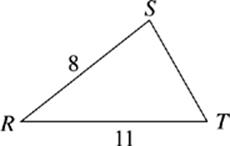
12. Which of the following expresses the possible values of p, if p is the perimeter of RST ?

(A) 3 < p < 19

(B) 3 < p < 22

(C) 19 < p < 22

(D) 19 < p < 38

(E) 22 < p < 38

17. An isosceles triangle has sides of lengths 5, 11, and x. How many possible values of x exist?

(A) One

(B) Two

(C) Three

(D) Four

(E) More than four

18. The distance between points A and D is 6, and the distance between D and F is 4. Which of the following is NOT a possible value for the distance between F and A ?

(A) 3

(B) 4

(C) 7

(D) 9

(E) 11

Right Triangles

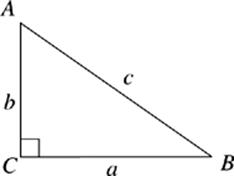
Right triangles are, not surprisingly, triangles that contain right angles. The sides of right triangles are referred to by special names. The sides that form the right angle are called the legs of the triangle and the longest side, opposite the right angle, is called the hypotenuse. There are many techniques and rules for right triangles that won”t work on just any triangle. The most important of these rules is the relationship between sides described by the Pythagorean theorem.

Pythagorean theorem

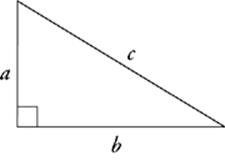
a² + b² = c²

Keep in mind when you use the Pythagorean theorem that the c always represents the hypotenuse.

DRILL

In the following triangles, use the Pythagorean theorem to fill in the missing sides of the triangles shown. The answers to these drills can be found in Chapter 12.

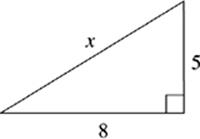
1. x = __________

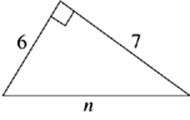
2. n = __________

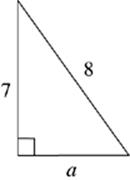
3. a = __________

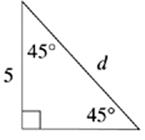
4. d = __________

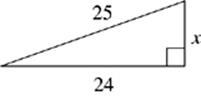
5. x = __________

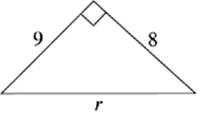
6. a = __________

Area of Triangles

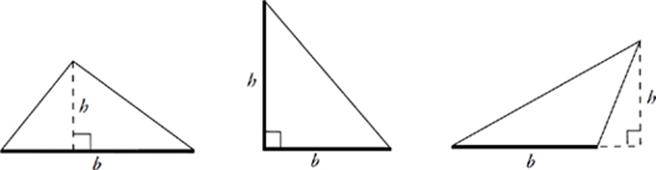
Area of a Triangle

A = bh

Notice that the height, or altitude, of a triangle can be inside the triangle, outside the triangle, or formed by a side of the triangle. In each case, the height is always perpendicular to the base. The height of a triangle must sometimes be computed with the Pythagorean theorem.

Area of an Equilateral Triangle

The height of an equilateral triangle can be found by dividing it into two 30°-60°-90° triangles, but you can save yourself the time and trouble if you memorize the following formula:

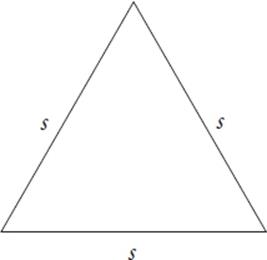
Area of an Equilateral Triangle

A =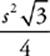

Trigonometry and the Area of a Triangle

On the Math Level 2, a useful formula that involves trigonometry is given by the following formula:

Area of a Triangle

A = ab sin θ

This formula is useful if you know the lengths of two sides of a triangle (a and b), and the measure of the angle between them (θ).

Trig Tricks

Later in this book you”ll
also use the basic functions
of trigonometry
to find the height of a
triangle. This formula will
come in handy for those
types of questions.

Drill

Try the following practice questions about the areas of triangles. The answers to these drills can be found in Chapter 12.

9. If the area of ∆ABC is equal to 3b, then a =

(A)

(B)

(C) 3

(D) 4

(E) 6

Note: Figure not drawn to scale

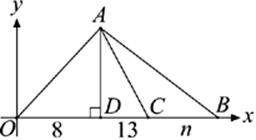
15. If ∆OAD and ∆ABC are of equal area, then n =

(A) 8

(B) 16

(C) 18

(D) 21

(E) 24

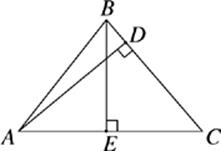
37. If AC = 12, BC = 10, and AD = 9, then BE =

(A) 7.0

(B) 7.5

(C) 8.0

(D) 8.5

(E) 9.0

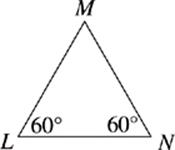
38. If ∆LMN has a perimeter of 24, then what is the area of ∆LMN ?

(A) 13.86

(B) 20.78

(C) 27.71

(D) 36.95

(E) 41.57

44. An equilateral triangle with an area of 12 has what perimeter?

(A) 12.00

(B) 13.39

(C) 15.59

(D) 15.79

(E) 18.66

46. A triangular traffic island with a flat surface is formed by the intersection of three streets. Two of the sides of the island have lengths of 6.4 meters and 10.8 meters. If the measure of the angle between these two sides is 55º, what is the area, in square meters, of the triangular surface of the island?

(A) 8.85

(B) 19.82

(C) 21.12

(D) 28.31

(E) 34.56

SPECIAL RIGHT TRIANGLES

Pythagorean Triplets

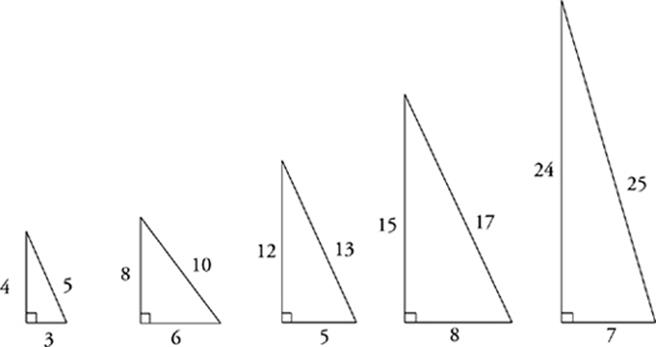
There are only a few right triangles whose sides all have integer lengths. These special triangles are called “Pythagorean triplets,” but that”s not important. What is important is that ETS puts these triangles on the test a lot. Memorize them and keep an eye out for them.

If a right triangle has two sides that fit the proportions of a Pythagorean triplet, then you can automatically fill in the third side. The multiples of these basic proportions will also be Pythagorean triplets. That means that 25-60-65 and 30-40-50 are also proportions of right triangles.

Triplet Families

Can you figure out the
original triplet that a
25-60-65 sided triangle
and a 30-40-50 sided
triangle came from? The
first is a multiple of a
5-12-13 right triangle, and
the second is a multiple of
a 3-4-5 right triangle.
This means that a
5-12-13 triangle is similar
to a 25-60-65 triangle. The
same is true of a
3-4-5 and a 30-40-50.
A little foreshadowing of
what we”ll discuss
in a page or two.

DRILL

Use the proportions of the Pythagorean triplets to complete the triangles below. The answers to these drills can be found in Chapter 12.

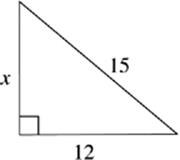
1. x = ___________

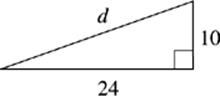
2. d = ___________

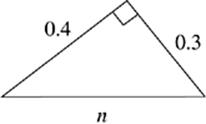
3. n = ___________

We”ve shown you some right triangles whose sides are in definite proportions. Now let”s look at some specific right triangles whose angles also create sides that are in definite proportions.

The 45°-45°-90° Triangle

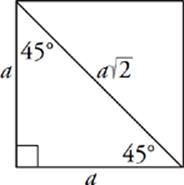
If you cut a square along its diagonal, you end up with two 45°-45°-90° triangles. Notice that this is an isosceles right triangle. The relation of the sides to the hypotenuse will always be the same.

The ratio of the sides of a 45°-45°-90° will always be a : a : a, where a is the length of one leg. The legs will be equal and the hypotenuse will always be equal to the length of a leg times . You can use this ratio for questions that ask for the length of either the leg or the hypotenuse. If the question gives you the length of the hypotenuse, just divide by to find the length of each leg.

Remember that you can use the Pythagorean theorem on most right triangle problems. However, if you recognize that a triangle is a 45°-45°-90°, this is a great shortcut to use to find the lengths.

DRILL

Use the proportions of the 45°-45°-90° triangle to complete the dimensions of the following triangles. The answers to these drills can be found in Chapter 12.

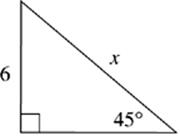
1. x = ______________

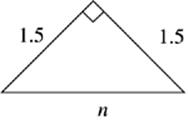
2. n = ______________

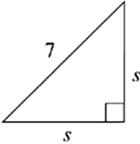
3. s = ______________

The 30°-60°-90° Triangle

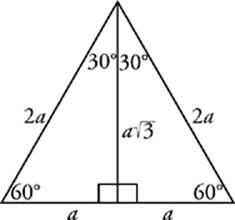
The altitude (height) of an equilateral triangle cuts it into two 30°-60°-90° triangles. As with 45°-45°-90° triangles, all right triangles with angles of 30°, 60°, and 90° have sides in a definite proportion. In a 30°-60°-90° triangle, the hypotenuse is twice as long as the shorter leg. The length of the longer leg is equal to the length of the shorter leg times . So the ratio of the sides is a : a : 2a where a is the length of the shorter leg of the triangle. If you are given the length of the longer leg, what can you do? That”s right, just divide the leg and the hypotenuse by .

What”s ETS Up To?

Remember that often
questions that appear
difficult at first just have
more steps to them. So
when ETS gives you a
square or an equilateral
triangle, see if it”s useful
to cut the shape and
use the formulas
we”ve given you.

DRILL

Use the proportions of the 30°-60°-90° triangles to complete the dimensions of the following triangles. The answers to these drills can be found in Chapter 12.

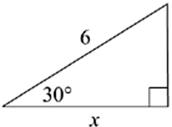
1. x = ______________

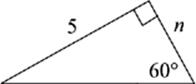
2. n = ______________

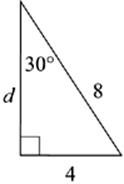
3. d = ______________

Drill

Use all of your right-triangle techniques to answer the following questions. The answers to these drills can be found in Chapter 12.

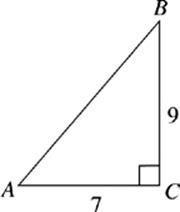
7. The perimeter of triangle ABC has how many possible values?

(A) One

(B) Two

(C) Three

(D) Four

(E) Infinitely many

13. A right triangle with a side of length 6 and a side of length 8 also has a side of length x. What is x ?

(A) 7

(B) 10

(C) 12

(D) 14

(E) It cannot be determined from the information given.

16. A straight 32-foot ladder is leaned against a vertical wall so that it forms a 30° angle with the wall. To what height in feet does the ladder reach?

(A) 9.24

(B) 16.00

(C) 27.71

(D) 43.71

(E) 54.43

19. An isosceles right triangle has a perimeter of 23.9. What is the area of this triangle?

(A) 16.9

(B) 24.5

(C) 25.0

(D) 33.8

(E) 49.0

Similar Triangles

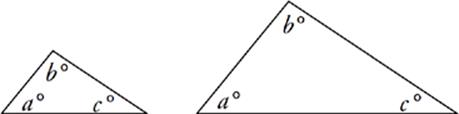
Triangles are said to be “similar” when they have the same angle measures. Basically, similar triangles have exactly the same shape, although they may be different sizes. Their sides, therefore, are in the same proportion.

Corresponding sides and heights of similar triangles are proportional.

For example, two 30°-60°-90° triangles of different sizes would be similar. If the short side of one triangle were twice as long as the short side of the other, then you could expect all of the larger triangle”s dimensions to be twice the smaller triangle”s dimensions. Similar triangles don”t have to be right triangles, however. Sides of triangles will be related proportionally whenever they have identical angle measures.

Proportionality

Here”s a quick reminder:
Not only are all
30°-60°-90° triangles
similar to each
other, but so are all
45°-45°-90° triangles.
Also, the Pythagorean
triplets that we
mentioned are similar to
their multiples.

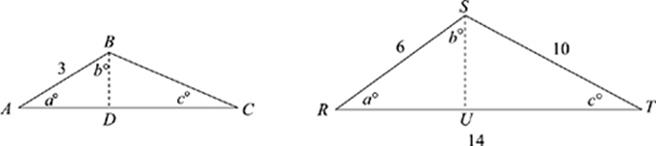
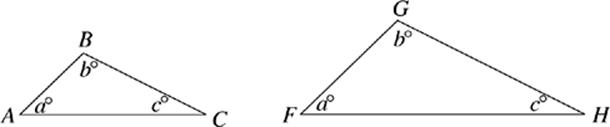
In the figure above, both triangles have angles measuring a, b, and c. Because they have the same angles, you know they”re similar triangles. Side RS of the large triangle and side AB of the smaller triangle are corresponding sides; each is the short side of its triangle. You can use the lengths of those two sides to figure out the proportion between the triangles. The length of AB is 3 and the length of RS is 6. So, RS is twice as long as AB. You can expect every side of RST to be twice as long as the corresponding side of ABC. That makes BC = 5 and AC = 7. Also, the height of triangle RST will be twice as long as the height of triangle ABC.

Similar Symbols

A similarity question
can say “Triangle ABC is
similar to Triangle DEF,” or
it can say that
∆ABC ∼ ∆DEF. These are
just two ways of saying
the same thing.

More Similarity

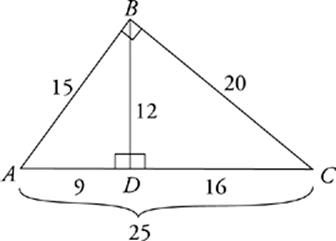
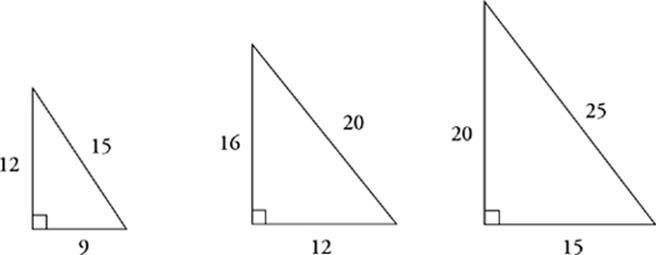
Whenever a right triangle is divided in two by a height drawn from the right angle, the result is three similar triangles of different sizes. The sides of the three triangles will be proportional. Let”s separate the triangles so you can see them more clearly.

DRILL

Use the proportionality of similar triangles to complete the dimensions of the triangles below. The answers to these drills can be found in Chapter 12.

1.

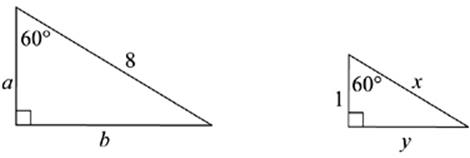
a =______________

b =______________

c =______________

d =______________

2.

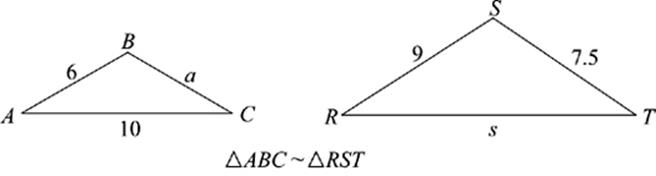
a =______________

s =______________

3.

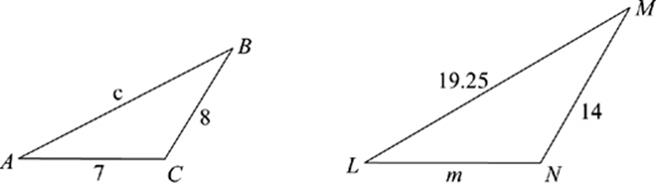
c =______________

m =______________

37. FG is twice as long as AB. If the area of triangle FGH is 0.5, what is the area of triangle ABC ?

(A) 0.13

(B) 0.25

(C) 0.50

(D) 1.00

(E) 2.00

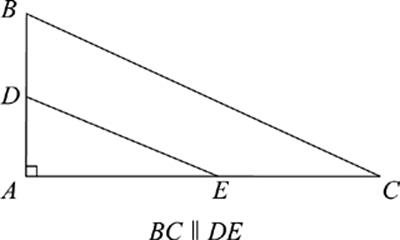
40. If the length of DB is half of the length of AD and BC || DE, then the area of triangle ADE is what fraction of the area of triangle ABC ?

(A)

(B)

(C)

(D)

(E)

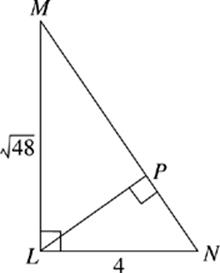
45. What is the area of ∆LPN ?

(A) 3.46

(B) 6.93

(C) 8.00

(D) 11.31

(E) 13.86

New Rule?

Can you figure out a rule
about the relationship
between the areas of
similar triangles?

QUADRILATERALS

A quadrilateral is any shape formed by four intersecting lines in a plane. The internal angle measures of a quadrilateral always add up to 360°.

Parallelograms

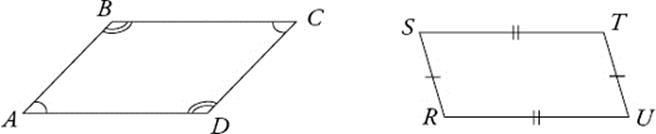
A parallelogram is a quadrilateral whose opposite sides are parallel. Rectangles are parallelograms, but a parallelogram does not need to have right angles. Note, however, that since the sides are parallel, Fred”s theorem applies to the angles of a parallelogram. Parallelograms have the following characteristics:

· Opposite angles in a parallelogram are equal.

· Adjacent angles in a parallelogram are supplementary; they add up to 180°, because of Fred”s theorem.

· Opposite sides in a parallelogram are of equal length.

· The diagonals of a parallelogram bisect each other.

The area of a parallelogram is given by this formula:

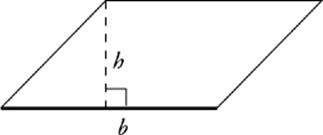
Connect the Dots

Notice that the area of a
parallelogram is twice the
area of a triangle. So you
can always figure out one
formula if you forget the
other!

Area of a Parallelogram

A = bh

If you know two adjacent sides of a parallelogram (a and b) and the angle between them (θ), you can use a formula involving trigonometry to find the area as well.

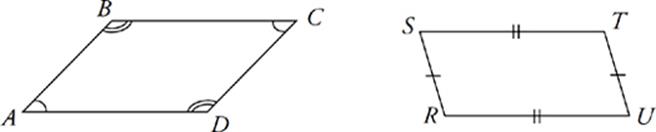
Height? There”s No
Height!

If you”re having trouble
finding the height in a
parallelogram involving
area, you can often use
Pythagorean theorem or
one of the special right
triangles.

Area of a Parallelogram

A = ab sin θ

Rectangles

A rectangle is just a parallelogram with four right angles. Rectangles have all the properties of parallelograms. In addition,

· each of the four interior angles measures 90°

· the diagonals of a rectangle are of equal length

Since all rectangles are parallelograms, the area of a rectangle is given by the same formula as that of a parallelogram.

Area of a Rectangle

A = bh

Squares

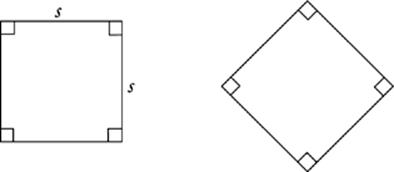
A square is a rectangle with four sides of equal length. (If you are asked to draw a rectangle, drawing a square is a legitimate response.)

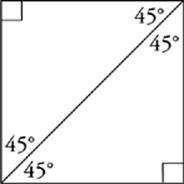
A diagonal in a square divides the square into two 45°-45°-90° triangles. The area of a square is given by either one of these formulas:

What”s with All This Memorization?!

Notice that the area of a
square, s², is just the base
times the height, which
is the formula for area of
a parallelogram and area
of a rectangle. Because
the base and height of
a square are the same,
we give you a shortcut
formula, but it”s really no
different from the others.
So, no need to memorize
it. You can always figure
it out!

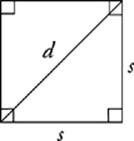
Area of a Square

A = s²

or

A =

The second, less-known formula for the area of a square can be used to shortcut questions that would otherwise take many more steps and require you to use a 45°-45°-90° triangle.

Trapezoids

A trapezoid is a quadrilateral whose top and bottom are parallel but differ in length.

The area of a trapezoid is given by the following formula:

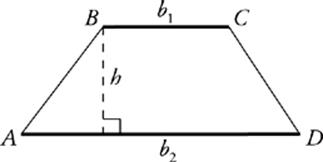
Area of a Trapezoid

A =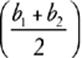

Drill

Try the following practice questions using quadrilateral formulas. The answers to these drills can be found in Chapter 12.

22. If AB = BC and DB = 5, then the area of ABCD =

(A) 12.50

(B) 14.43

(C) 17.68

(D) 35.36

(E) 43.30

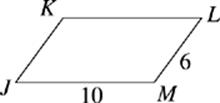
34. If the measure of ∠DBC and ∠KJM is 60°, what is the area of parallelogram JKLM ?

(A) 18.34

(B) 25.98

(C) 34.64

(D) 51.96

(E) 60.00

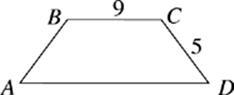
40. The bases of trapezoid ABCD differ in length by 6, and the perimeter of the trapezoid is 34. What is the area of ABCD ?

(A) 45.0

(B) 48.0

(C) 54.0

(D) 60.0

(E) 62.5

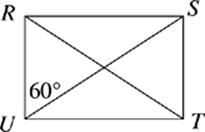
45. If the area of rectangle RSTU is 62.35, then RT + SU =

(A) 18.8

(B) 24.0

(C) 32.0

(D) 36.0

(E) 40.8

OTHER POLYGONS

The Math Subject Tests may occasionally require you to deal with polygons other than triangles and quadrilaterals. Here are the names of the other polygons you”re likely to see:

pentagon: a five-sided polygon

hexagon: a six-sided polygon

heptagon: a seven-sided polygon

octagon: an eight-sided polygon

All of the polygons pictured above are regular polygons. That means that their sides and angles are all of the same size.

You know that the internal angles of a triangle add up to 180° and that the internal angles of a quadrilateral add up to 360°. But what about the angles of a hexagon or an octagon? You can compute the sum of a polygon”s internal angles using this formula:

Sum of the Angles of an n-sided Polygon

Sum of Angles = (n − 2) × 180°

Using this formula, you can figure out that the angles of a hexagon (a 6-sided figure) would have a sum of (4 × 180) degrees. That”s 720°. If you know that the figure is a regular hexagon, then you can even figure out the measure of each angle: 720° ÷ 6 = 120°.

Just Make Triangles!

This formula may seem random and now you”re stressing about all the memorizing you”re going to have to do. But in reality, you don”t have to know the formula. Now you”re saying “What?! If we don”t have to know it, why are we memorizing it?!” There are almost always ways around knowing formulas. It”s great if you can memorize this, but if you can”t, then count the triangles! Start at one vertex of the polygon you”re looking at and create triangles by drawing a line from that same vertex to every other vertex in the figure, like this:

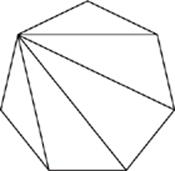
Now just count the triangles. For our picture, there are 5 triangles. You already know that there are 180° in a triangle. So there must be 5 × 180°, or 900°, in the polygon. Notice that 5 is 7 − 2 and 180 is just the number of degrees in a triangle. Funny, you just created the formula for the sum of the angles in a polygon!

CIRCLES

A circle is defined as the set of all the points located at a certain distance from a given center point. A point that is said to be on a circle is a point on the edge of the circle, not contained within the circle.

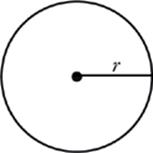
The radius is the distance from the center to the edge of the circle.

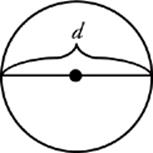
The diameter of a circle is the distance from edge to edge through the circle”s center. The diameter is twice as long as the radius.

The circumference of a circle is the distance around the circle—essentially, the circle”s perimeter. The circumference is given by the following formula:

Circumference of a Circle

C = πd or C = 2πr

The area of a circle is given by the following formula:

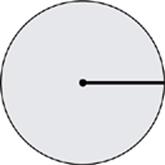
Area of a Circle

A = πr²

DRILL

Use formulas to complete the dimensions of the following circles. The answers to these drills can be found in Chapter 12.

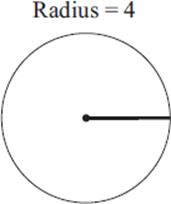
1. C =______________

 A =______________

2. C =______________

 r =______________

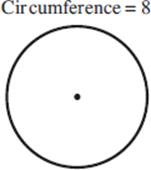
3. A =______________

 r =______________

A Slice of Pie

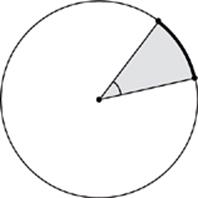
The portion of a circle”s area between two radii is called a sector. The portion of the circle”s circumference that falls between the radii is called an arc. Between any two points on a circle”s edge, there are two arcs, a major arc and a minor arc. The minor arc is the shorter of the two, and it”s usually the one ETS is concerned about.

The angle between two radii is called a central angle. The degree measure of a central angle is equal to the degree measure of the arc that it cuts out of the circle”s circumference. In other words, the minor arc formed by a 40˚ central angle is a 40˚ arc.

To put it simply, the piece of a circle defined by a central angle (like a slice of pie) takes the same fraction of everything. A 60˚ central angle, for instance, takes one-sixth of the circle”s 360˚; the arc that is formed will be one-sixth of the circumference; the sector that is formed will be one-sixth of the circle”s area. In other words:

• Area = Sector and • Circumference = Arc

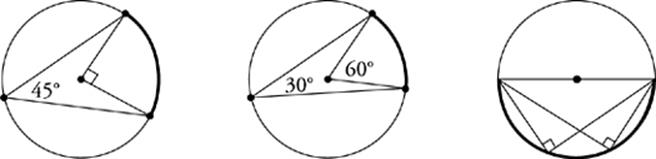
Inscribed Angles

Same Segments

All angles inscribed in the
same segment of a circle
(or identical circles) are
equal.

An angle formed by two chords (lines drawn from any point on the circle to any other point on the circle) is called an inscribed angle. While a central angle with a certain degree measure intercepts an arc of the same degree measure, an inscribed angle intercepts an arc with twice the degree measure of the angle. For example, a 30˚ central angle intercepts a 30˚ arc, while a 30˚ inscribed angle intercepts a 60˚ arc.

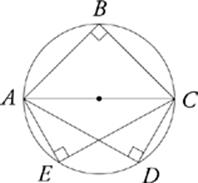
Any time you draw two lines, one from each endpoint of the diameter, to the same point on the semicircle, the lines will meet at a right angle. In other words, any angle inscribed in a semicircle is a right angle.

Tangent Lines

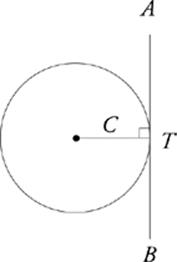
A tangent line to a circle is a line that touches the circle at only one point. A tangent line is always perpendicular to the radius touching the same point.

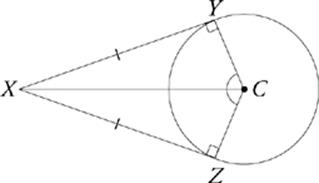
From any point outside a circle, there are two separate tangent lines to that circle. The distances to the two points of tangency are equal, and the radii to the points of tangency make equal angles with the line connecting the external point to the circle”s center.

Drill

Try the following practice questions using the rules and techniques for circles. The answers to these drills can be found in Chapter 12.

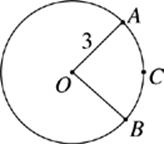
Note: Figure not drawn to scale

12. In the circle with center O, if the length of minor arc ACB is 4.71, which of the following best approximates the measure of ∠AOB ?

(A) 60.0°

(B) 72.0°

(C) 86.4°

(D) 90.0°

(E) 98.6°

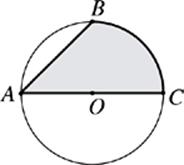
29. If the circle with center O has a radius of 5 and the measure of ∠BAC is 45°, then what is the area of the shaded region?

(A) 32.13

(B) 31.52

(C) 26.70

(D) 25.41

(E) 24.26

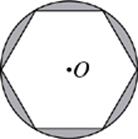
31. A regular hexagon is inscribed in the circle with center O. If the circle has a radius of 4, what is the area of the shaded region?

(A) 8.3

(B) 8.7

(C) 9.0

(D) 9.4

(E) 10.2

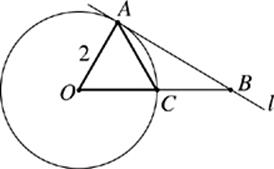
43. Line l is tangent to the circle with center O at A, and OA = AC. What is the length of AB ?

(A) 1.73

(B) 2.83

(C) 3.46

(D) 4.74

(E) 5.20

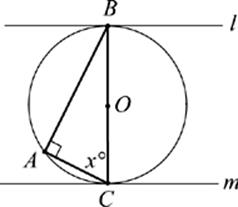
Note: Figure not drawn to scale.

45. The right angle CAB is inscribed in the circle with center O and diameter BC. Lines l and m are tangent to the circle at B and C, respectively. Which of the following must be true?

I. AB < BC

II. x = 60

III. l and m meet when extended to the right.

(A) I only

(B) III only

(C) I and II only

(D) II and III only

(E) I, II, and III

Summary

· Plane geometry appears on the Level 1 Math Subject Test, but it”s a useful knowledge base for those taking the Level 2 Test as well.

· Some rules about lines and angles:

· A 90° angle is formed by two lines perpendicular to each other.

· There are 180° in a line.

· When two straight lines intersect, the angles created opposite each other are equal. The adjacent angles (two angles beside each other along the same straight line) have a sum of 180°.

· Fred”s theorem states that when parallel lines are crossed by a third line, big angles and small angles are created. All the big angles are equal, all the small angles are equal, and a big plus a small equals 180°.

· Triangles form the largest set of plane geometry questions on the test.

· The sum of the angles in a triangle is 180°.

· The longest side of a triangle is across from the largest angle. The smallest side of a triangle is across from the smallest angle. Equal sides are across from equal angles.

· Isosceles triangles have at least two equal sides and two equal angles. Equilateral triangles have three equal sides and three equal angles.

· The third side rule states that the length of any side of a triangle must be between the sum and the difference of the other two sides.

· The area of a triangle is A = bh. The height must be perpendicular to the base.

· Right triangles are triangles with one 90° angle. The Pythagorean theorem states that, in a right triangle, a² + b² = c², where c is the hypotenuse of the triangle and a and b are the two legs.

· Special right triangles are helpful in simplifying the math. They often provide an easier route to the correct solution than using the Pythagorean theorem, so look closely for opportunities to use them. The following is a list of special right triangles:

· There are some Pythagorean triplets that are helpful to have in your back pocket. They are 3-4-5, 5-12-13, 7-24-25, and any multiples of these as well.

· The sides of a 45°-45°-90° triangle have a very specific ratio: x : x : x, where x is the length of each leg.

· The sides of a 30°-60°-90° triangle have a very specific ratio: x : x : 2x, where x is the length of the shorter leg.

· Similar triangles have the same angle measures. The corresponding sides and heights of similar triangles are proportional.

· Quadrilaterals are four-sided figures. The sum of the angles in a quadrilateral is 360°.

· Parallelograms have two sets of equal, parallel lines. The area of a parallelogram is A = bh, where the base is perpendicular to the height.

· Rectangles are parallelograms with four right angles.

· Squares are rectangles with four equal sides.

· Trapezoids are four-sided figures whose top and bottom are parallel but different in length. The area of a trapezoid is A = 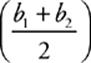h, where b₁ is one base and b₂ is the other.

· The sum of the angles of an n-sided polygon is (n − 2) × 180°.

· Here are some things to remember about a circle:

· A circle contains a total of 360°.

· The radius is the distance from the center of the circle to any point on the circle.

· The diameter is a straight line drawn from one point on a circle through the center to another. Its length is twice the radius.

· The circumference of the circle is the distance around the circle. You can think of it as the perimeter of the circle. Its formula is C = πd. You may also know it as C = 2πr.

· The formula for area of a circle is A =πr².

· A sector is a slice of pie of the circle. The part of the circumference that the sector contains is called an arc and is in the same proportion to the circumference as the angle of the sector is to 360°.

· A central angle is an angle whose vertex is the center of the circle. An inscribed angle has its vertex on the circle and its two endpoints on the circle. Its angle is half of what the central angle is to those same two endpoints.

· Any angle inscribed in a semicircle is a right angle.

· A line tangent to the circle touches the circle in only one place and is always perpendicular to the radius drawn to the point of tangency.

· Some information for Level 2 test takers:

· The area of a triangle, using trigonometry, is A = ab sinθ

· The area of a parallelogram, using trigonometry, is A = ab sin θ.