Barron's SAT Subject Test Math Level 2, 10th Edition (2012)

Part 2. REVIEW OF MAJOR TOPICS

Chapter 3. Numbers and Operations

3.2 Complex Numbers

IMAGINARY NUMBERS

The square of a real number is never negative. This means that the square root of a negative number cannot be a real number. The symbol is called the imaginary unit, i² = –1. Powers of i follow a pattern:

In other words, powers of i follow a cycle of four. This means that iⁿ = i^{n mod 4}, where n mod 4 is the remainder when n is divided by 4. For example, i ⁵⁸ = i² = –1.

The imaginary numbers are numbers of the form bi , where b is a real number. The square root of any negative number is i times the square root of the positive of that number. Thus for example, , and .

EXERCISE

1. i²⁹ =

 (A) 1

 (B) i

 (C) –i

 (D) –1

 (E) none of these

COMPLEX NUMBER ARITHMETIC

The complex numbers are formed by “attaching” imaginary numbers to real numbers using a plus sign (+). The standard form of a complex number is a + bi , where a and b are real. The number a is called the real part of the complex number, and the b number is called the imaginary part. If b = 0, then the complex number is just a real number. If b 0, the complex number is called imaginary. If a = 0, bi is called a pure imaginary number. Examples of imaginary numbers are 2 + 3i, – + 4i, 6i, 0.11 + (–0.45)i, and – i.

When the imaginary part of a complex number is a radical, write the i to the left in order to avoid ambiguity about whether i is under the radical.

Finding sums, differences, products, quotients, and reciprocals of complex numbers can be accomplished directly on your calculator. The imaginary unit i is 2nd decimal point. If you enter an expression with i in it, the calculator will do imaginary arithmetic in REAL mode. If the expression entered does not include i but the output is imaginary, the calculator gives you the error message NONREAL ANS. For example, if you tried to calculate in REAL mode, you would get this error message. In a + bi mode, would calculate as 1.732···i . You should use a + bi mode exclusively for the Level 2 test. Although complex number arithmetic per se is not likely to be on a Level 2 test, an understanding of how it is done may be. A review of the main features of complex number arithmetic is provided in the next several paragraphs.

To add or subtract complex numbers, add or subtract their real and imaginary parts. For example,

(5 – 7i ) + (2 + 4i ) = 7 – 3i .

To multiply complex numbers, multiply like you would any two binomial expressions, using FOIL. Thus

(a + bi )(c + di ) = ac + adi + bci + bdi ² = (ac – bd ) + (ad + bc )i .

The difference of the first and last terms makes the real part, and the sum of the outer and inner terms makes the imaginary part.

To find the quotient of two complex numbers, multiply the denominator and numerator by the conjugate of the denominator. Then simplify. For example,

EXERCISES

1. Write the product of (2 + 3i )(4 – 5i ) in standard form.

 (A) –7 – 23i

 (B) –7 + 2i

 (C) 23 – 7i

 (D) 23 + 2i

 (E) 23 – 2i

2. Write in standard form.

 (A)

 (B)

 (C)

 (D) –1 + 2i

 (E) –1–2i

3. If z = 8 – 2i , z ² =

 (A) 60 − 32i

 (B) 64 + 4i

 (C) 64–4i

 (D) 60

 (E) 68

GRAPHING COMPLEX NUMBERS

A complex number can be represented graphically as rectangular coordinates, with the x -coordinate as the real part and the y -coordinate as the imaginary part. The modulus of a complex number is the square of its distance to the origin. The Pythagorean theorem tells us that this distance is . The conjugate of the imaginary number a + bi is a – bi , so the graphs of conjugates are reflections about the y -axis. Also, the product of an imaginary number and its conjugate is the square of the modulus because (a + bi )(a – bi ) = a ² – b ²i ² = a ² + b².

EXERCISES

1. If z is the complex number shown in the figure, which of the following points could be iz?

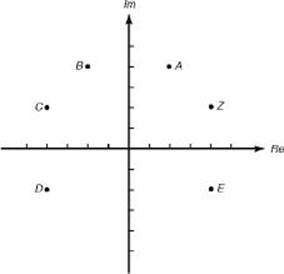
 (A) A

 (B) B

 (C) C

 (D) D

 (E) E

2. Which of the following is the modulus of 2 + i?

 (A)

 (B) 2

 (C)

 (D)

 (E) 5

Answers and Explanations

Imaginary Numbers

1. (B) i²⁹ = i¹ = i.

Complex Number Arithmetic

1. (D) If you enter imaginary numbers into the calculator, it will do imaginary arithmetic without changing mode. The imaginary unit is 2nd decimal point. Enter the product, and read the solution 23 + 2i .

2. * (C) Simply enter the expression into the graphing calculator.

3. * (A) Simply enter the expression into the graphing calculator.

Graphing Complex Numbers

1. (B) z = 4 + 2i , so iz = –2 + 4i , which is point B .

2. (D) The real and imaginary parts are 2 and 1, respectively, so the modulus is .